在ZDT3问题上基于多目标超体积的蚁群优化基准测试#
在本教程中,我们将展示如何使用pygmo运行maco算法,并使用Zitzler、Deb和Thiele(ZDT)测试问题套件中的第3个问题进行基准测试,该问题通常用于在两个目标问题上对多目标算法进行基准测试。
ZDT3问题是一个盒约束的连续双目标问题,由pygmo在zdt类中作为UDP(用户定义问题)提供。
我们现在想要对三种用户定义的算法进行基准测试。由于这是一个多目标问题,我们需要一个能够处理约束的UDA(用户定义算法)。因此,我们将对多目标蚁群优化算法maco、基于分解的多目标进化算法(MOEA/D)moead以及非支配排序遗传算法(NSGA-II)nsga2进行基准测试。
特别是,我们将使用上述三种UDAs,分别采用三种不同的人口规模(即32、64、128),并且每次模拟运行三次(每次使用不同的固定种子)。这个问题的Pareto前沿是已知的,pygmo.zdt问题集中的问题实现了一个称为p_distance的收敛度量,它允许我们检查非支配前沿覆盖已知Pareto前沿的程度。此外,我们将使用hypervolume的概念作为指标来比较不同算法的最终种群。
为了在这些问题上运行UDAs,我们可以编写以下代码:
>>> from pygmo import *
>>> import numpy as np
>>> from matplotlib import pyplot as plt
>>> pop_sizes=[32, 64, 128]
>>> udp = zdt(prob_id = 3)
>>> hv_moead=[0, 0, 0]
>>> hv_maco=[0, 0, 0]
>>> hv_nsga2=[0, 0, 0]
>>> p_dist_moead=[0, 0, 0]
>>> p_dist_maco=[0, 0, 0]
>>> p_dist_nsga2=[0, 0, 0]
>>> #We run the algos three times each, for 3 different pop-sizes
>>> for j in pop_sizes:
... for i in range(0,3):
... pop_1 = population(prob = udp, size = j, seed = i)
... pop_2 = population(prob = udp, size = j, seed = i)
... pop_3 = population(prob = udp, size = j, seed = i)
...
... hv=hypervolume(pop_1)
... ref_point=hv.refpoint(offset=0.01)
...
... #I store all the pop-sizes results for all the runs:
... #1st seed:
... if j==pop_sizes[0] and i==0:
... first_pop_32_1=pop_1.get_f()
... if j==pop_sizes[1] and i==0:
... first_pop_64_1=pop_1.get_f()
... if j==pop_sizes[2] and i==0:
... first_pop_128_1=pop_1.get_f()
...
... #2nd seed:
... if j==pop_sizes[0] and i==1:
... first_pop_32_2=pop_1.get_f()
... if j==pop_sizes[1] and i==1:
... first_pop_64_2=pop_1.get_f()
... if j==pop_sizes[2] and i==1:
... first_pop_128_2=pop_1.get_f()
...
... #3rd seed:
... if j==pop_sizes[0] and i==2:
... first_pop_32_3=pop_1.get_f()
... if j==pop_sizes[1] and i==2:
... first_pop_64_3=pop_1.get_f()
... if j==pop_sizes[2] and i==2:
... first_pop_128_3=pop_1.get_f()
...
... algo = algorithm(moead(250, 'random'))
... algo_2 = algorithm(maco(gen = 250, ker = j-20, q = 1.0, threshold = 250, n_gen_mark = 47, evalstop=10000, focus=0.0, memory=False))
... algo_3 = algorithm(nsga2(gen = 250))
... algo.set_seed(i+1)
... algo_2.set_seed(i+1)
... algo_3.set_seed(i+1)
... pop_1 = algo.evolve(pop_1)
... pop_2=algo_2.evolve(pop_2)
... pop_3 = algo_3.evolve(pop_3)
...
... #This returns a series of arrays: in each of them it is contained (in this order), the -non-dominated front, -domination list,
... #-domination count, -non-domination rank
... fnds=fast_non_dominated_sorting(pop_1.get_f())
... fnds_2=fast_non_dominated_sorting(pop_2.get_f())
... fnds_3=fast_non_dominated_sorting(pop_3.get_f())
...
... #This returns the first (i.e., best) non-dominated front:
... first_ndf_moead=fnds[0][0]
... first_ndf_maco=fnds_2[0][0]
... first_ndf_nsga2=fnds_3[0][0]
...
... #I store all the pop-sizes non-dominated fronts for all the runs:
... #1st seed:
... if j==pop_sizes[0] and i==0:
... #MOEA/D
... hv_moead[0]=hypervolume(pop_1).compute(ref_point)
... p_dist_moead[0]=udp.p_distance(pop_1)
... first_col_moead_32_1=pop_1.get_f()[first_ndf_moead,0]
... second_col_moead_32_1=pop_1.get_f()[first_ndf_moead,1]
... #MACO
... hv_maco[0]=hypervolume(pop_2).compute(ref_point)
... p_dist_maco[0]=udp.p_distance(pop_2)
... first_col_maco_32_1=pop_2.get_f()[first_ndf_maco,0]
... second_col_maco_32_1=pop_2.get_f()[first_ndf_maco,1]
... #NSGA2
... hv_nsga2[0]=hypervolume(pop_3).compute(ref_point)
... p_dist_nsga2[0]=udp.p_distance(pop_3)
... first_col_nsga2_32_1=pop_3.get_f()[first_ndf_nsga2,0]
... second_col_nsga2_32_1=pop_3.get_f()[first_ndf_nsga2,1]
...
... if j==pop_sizes[1] and i==0:
... #MOEA/D
... hv_moead[1]=hypervolume(pop_1).compute(ref_point)
... p_dist_moead[1]=udp.p_distance(pop_1)
... hv_moead[1]=hypervolume(pop_1).compute(ref_point)
... p_dist_moead[1]=udp.p_distance(pop_1)
... first_col_moead_64_1=pop_1.get_f()[first_ndf_moead,0]
... second_col_moead_64_1=pop_1.get_f()[first_ndf_moead,1]
... #MACO
... hv_maco[1]=hypervolume(pop_2).compute(ref_point)
... p_dist_maco[1]=udp.p_distance(pop_2)
... first_col_maco_64_1=pop_2.get_f()[first_ndf_maco,0]
... second_col_maco_64_1=pop_2.get_f()[first_ndf_maco,1]
... #NSGA2
... hv_nsga2[1]=hypervolume(pop_3).compute(ref_point)
... p_dist_nsga2[1]=udp.p_distance(pop_3)
... first_col_nsga2_64_1=pop_3.get_f()[first_ndf_nsga2,0]
... second_col_nsga2_64_1=pop_3.get_f()[first_ndf_nsga2,1]
...
... if j==pop_sizes[2] and i==0:
... #MOEA/D
... hv_moead[2]=hypervolume(pop_1).compute(ref_point)
... p_dist_moead[2]=udp.p_distance(pop_1)
... first_col_moead_128_1=pop_1.get_f()[first_ndf_moead,0]
... second_col_moead_128_1=pop_1.get_f()[first_ndf_moead,1]
... #MACO
... hv_maco[2]=hypervolume(pop_2).compute(ref_point)
... p_dist_maco[2]=udp.p_distance(pop_2)
... first_col_maco_128_1=pop_2.get_f()[first_ndf_maco,0]
... second_col_maco_128_1=pop_2.get_f()[first_ndf_maco,1]
... #NSGA2
... hv_nsga2[2]=hypervolume(pop_3).compute(ref_point)
... p_dist_nsga2[2]=udp.p_distance(pop_3)
... first_col_nsga2_128_1=pop_3.get_f()[first_ndf_nsga2,0]
... second_col_nsga2_128_1=pop_3.get_f()[first_ndf_nsga2,1]
...
... #2nd seed:
... if j==pop_sizes[0] and i==1:
... #MOEA/D
... hv_moead[0]+=hypervolume(pop_1).compute(ref_point)
... p_dist_moead[0]+=udp.p_distance(pop_1)
... first_col_moead_32_2=pop_1.get_f()[first_ndf_moead,0]
... second_col_moead_32_2=pop_1.get_f()[first_ndf_moead,1]
... #MACO
... hv_maco[0]+=hypervolume(pop_2).compute(ref_point)
... p_dist_maco[0]+=udp.p_distance(pop_2)
... first_col_maco_32_2=pop_2.get_f()[first_ndf_maco,0]
... second_col_maco_32_2=pop_2.get_f()[first_ndf_maco,1]
... #NSGA2
... hv_nsga2[0]+=hypervolume(pop_3).compute(ref_point)
... p_dist_nsga2[0]+=udp.p_distance(pop_3)
... first_col_nsga2_32_2=pop_3.get_f()[first_ndf_nsga2,0]
... second_col_nsga2_32_2=pop_3.get_f()[first_ndf_nsga2,1]
...
... if j==pop_sizes[1] and i==1:
... #MOEA/D
... hv_moead[1]+=hypervolume(pop_1).compute(ref_point)
... p_dist_moead[1]+=udp.p_distance(pop_1)
... first_col_moead_64_2=pop_1.get_f()[first_ndf_moead,0]
... second_col_moead_64_2=pop_1.get_f()[first_ndf_moead,1]
... #MACO
... hv_maco[1]+=hypervolume(pop_2).compute(ref_point)
... p_dist_maco[1]+=udp.p_distance(pop_2)
... first_col_maco_64_2=pop_2.get_f()[first_ndf_maco,0]
... second_col_maco_64_2=pop_2.get_f()[first_ndf_maco,1]
... #NSGA2
... hv_nsga2[1]+=hypervolume(pop_3).compute(ref_point)
... p_dist_nsga2[1]+=udp.p_distance(pop_3)
... first_col_nsga2_64_2=pop_3.get_f()[first_ndf_nsga2,0]
... second_col_nsga2_64_2=pop_3.get_f()[first_ndf_nsga2,1]
...
... if j==pop_sizes[2] and i==1:
... #MOEA/D
... hv_moead[2]+=hypervolume(pop_1).compute(ref_point)
... p_dist_moead[2]+=udp.p_distance(pop_1)
... first_col_moead_128_2=pop_1.get_f()[first_ndf_moead,0]
... second_col_moead_128_2=pop_1.get_f()[first_ndf_moead,1]
... #MACO
... hv_maco[2]+=hypervolume(pop_2).compute(ref_point)
... p_dist_maco[2]+=udp.p_distance(pop_2)
... first_col_maco_128_2=pop_2.get_f()[first_ndf_maco,0]
... second_col_maco_128_2=pop_2.get_f()[first_ndf_maco,1]
... #NSGA2
... hv_nsga2[2]+=hypervolume(pop_3).compute(ref_point)
... p_dist_nsga2[2]+=udp.p_distance(pop_3)
... first_col_nsga2_128_2=pop_3.get_f()[first_ndf_nsga2,0]
... second_col_nsga2_128_2=pop_3.get_f()[first_ndf_nsga2,1]
...
... #3rd seed:
... if j==pop_sizes[0] and i==2:
... #MOEA/D
... hv_moead[0]+=hypervolume(pop_1).compute(ref_point)
... p_dist_moead[0]+=udp.p_distance(pop_1)
... first_col_moead_32_3=pop_1.get_f()[first_ndf_moead,0]
... second_col_moead_32_3=pop_1.get_f()[first_ndf_moead,1]
... #MACO
... hv_maco[0]+=hypervolume(pop_2).compute(ref_point)
... p_dist_maco[0]+=udp.p_distance(pop_2)
... first_col_maco_32_3=pop_2.get_f()[first_ndf_maco,0]
... second_col_maco_32_3=pop_2.get_f()[first_ndf_maco,1]
... #NSGA2
... hv_nsga2[0]+=hypervolume(pop_3).compute(ref_point)
... p_dist_nsga2[0]+=udp.p_distance(pop_3)
... first_col_nsga2_32_3=pop_3.get_f()[first_ndf_nsga2,0]
... second_col_nsga2_32_3=pop_3.get_f()[first_ndf_nsga2,1]
...
... if j==pop_sizes[1] and i==2:
... #MOEA/D
... hv_moead[1]+=hypervolume(pop_1).compute(ref_point)
... p_dist_moead[1]+=udp.p_distance(pop_1)
... first_col_moead_64_3=pop_1.get_f()[first_ndf_moead,0]
... second_col_moead_64_3=pop_1.get_f()[first_ndf_moead,1]
... #MACO
... hv_maco[1]+=hypervolume(pop_2).compute(ref_point)
... p_dist_maco[1]+=udp.p_distance(pop_2)
... first_col_maco_64_3=pop_2.get_f()[first_ndf_maco,0]
... second_col_maco_64_3=pop_2.get_f()[first_ndf_maco,1]
... #NSGA2
... hv_nsga2[1]+=hypervolume(pop_3).compute(ref_point)
... p_dist_nsga2[1]+=udp.p_distance(pop_3)
... first_col_nsga2_64_3=pop_3.get_f()[first_ndf_nsga2,0]
... second_col_nsga2_64_3=pop_3.get_f()[first_ndf_nsga2,1]
...
... if j==pop_sizes[2] and i==2:
... #MOEA/D
... hv_moead[2]+=hypervolume(pop_1).compute(ref_point)
... p_dist_moead[2]+=udp.p_distance(pop_1)
... first_col_moead_128_3=pop_1.get_f()[first_ndf_moead,0]
... second_col_moead_128_3=pop_1.get_f()[first_ndf_moead,1]
... #MACO
... hv_maco[2]+=hypervolume(pop_2).compute(ref_point)
... p_dist_maco[2]+=udp.p_distance(pop_2)
... first_col_maco_128_3=pop_2.get_f()[first_ndf_maco,0]
... second_col_maco_128_3=pop_2.get_f()[first_ndf_maco,1]
... #NSGA2
... hv_nsga2[2]+=hypervolume(pop_3).compute(ref_point)
... p_dist_nsga2[2]+=udp.p_distance(pop_3)
... first_col_nsga2_128_3=pop_3.get_f()[first_ndf_nsga2,0]
... second_col_nsga2_128_3=pop_3.get_f()[first_ndf_nsga2,1]
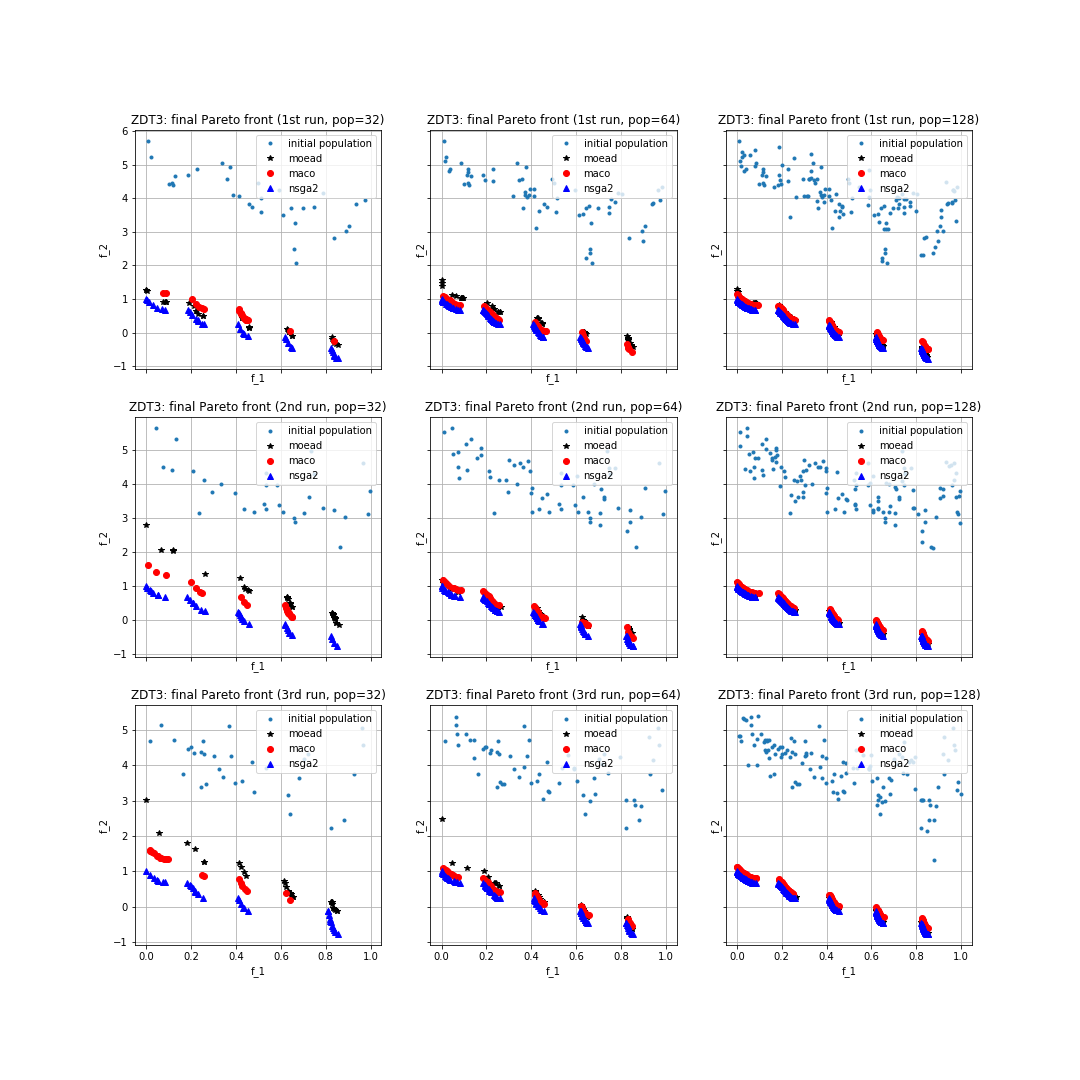
正如我们从python脚本中观察到的,我们正在使用三种不同的种群大小(32、64、128)运行三种算法250代,并存储最终的非支配Pareto前沿以及最终种群的超体积和p距离值。 我们现在可以在适应度空间中绘制结果(即,通过在y轴上绘制第二个适应度值,在x轴上绘制第一个适应度值)。此外,我们将打印三种算法和所有种群大小的超体积和p距离值的三次运行的平均值。特别是,向量的第一个元素对应于种群大小32的三次运行的平均值,第二个元素对应于种群大小64的平均值,第三个元素对应于128的平均值。为此,我们编写了以下代码:
>>> print('\n joint hypervolume MOEA/D :\n')
>>> print(np.array(hv_moead)/3)
>>> print('\n joint hypervolume MACO: \n')
>>> print(np.array(hv_maco)/3)
>>> print('\n joint hypervolume NSGA2: \n')
>>> print(np.array(hv_nsga2)/3)
>>> print('\n p-distance MOEA/D: \n')
>>> print(np.array(p_dist_moead)/3)
>>> print('\n p-distance MACO: \n')
>>> print(np.array(p_dist_maco)/3)
>>> print('\n p-distance NSGA-II: \n')
>>> print(np.array(p_dist_nsga2)/3)
joint hypervolume MOEA/D:
[4.68242751 5.2765971 5.57259658]
joint hypervolume MACO:
[4.74695083 5.38002359 5.49987744]
joint hypervolume NSGA2:
[5.45305456 5.58634807 5.65456127]
p-distance MOEA/D:
[0.98580786 0.43830665 0.11202489]
p-distance MACO:
[0.75737982 0.27526069 0.21809924]
p-distance NSGA-II:
[0.01847673 0.00465985 0.00137918]
>>> fig, axes = plt.subplots(nrows=3, ncols=3, sharex='col', sharey='row', figsize=(15,15))
>>> axes[0,0].plot(first_pop_32_1[:,0], first_pop_32_1[:,1], '.', label= 'initial population')
>>> axes[0,0].plot(first_col_moead_32_1, second_col_moead_32_1,'k*', label = 'moead')
>>> axes[0,0].plot(first_col_maco_32_1, second_col_maco_32_1,'ro', label = 'maco')
>>> axes[0,0].plot(first_col_nsga2_32_1, second_col_nsga2_32_1, 'b^', label = 'nsga2')
>>> axes[0,0].legend(loc='upper right')
>>> axes[0,0].set_title('ZDT3: final Pareto front (1st run, pop=32)')
>>> axes[0,1].plot(first_pop_64_1[:,0], first_pop_64_1[:,1], '.', label= 'initial population')
>>> axes[0,1].plot(first_col_moead_64_1, second_col_moead_64_1,'k*', label = 'moead')
>>> axes[0,1].plot(first_col_maco_64_1, second_col_maco_64_1,'ro', label = 'maco')
>>> axes[0,1].plot(first_col_nsga2_64_1, second_col_nsga2_64_1, 'b^', label = 'nsga2')
>>> axes[0,1].legend(loc='upper right')
>>> axes[0,1].set_title('ZDT3: final Pareto front (1st run, pop=64)')
>>> axes[0,2].plot(first_pop_128_1[:,0], first_pop_128_1[:,1], '.', label= 'initial population')
>>> axes[0,2].plot(first_col_moead_128_1, second_col_moead_128_1,'k*', label = 'moead')
>>> axes[0,2].plot(first_col_maco_128_1, second_col_maco_128_1,'ro', label = 'maco')
>>> axes[0,2].plot(first_col_nsga2_128_1, second_col_nsga2_128_1, 'b^', label = 'nsga2')
>>> axes[0,2].legend(loc='upper right')
>>> axes[0,2].set_title('ZDT3: final Pareto front (1st run, pop=128)')
>>> axes[1,0].plot(first_pop_32_2[:,0], first_pop_32_2[:,1], '.', label= 'initial population')
>>> axes[1,0].plot(first_col_moead_32_2, second_col_moead_32_2,'k*', label = 'moead')
>>> axes[1,0].plot(first_col_maco_32_2, second_col_maco_32_2,'ro', label = 'maco')
>>> axes[1,0].plot(first_col_nsga2_32_2, second_col_nsga2_32_2, 'b^', label = 'nsga2')
>>> axes[1,0].legend(loc='upper right')
>>> axes[1,0].set_title('ZDT3: final Pareto front (2nd run, pop=32)')
>>> axes[1,1].plot(first_pop_64_2[:,0], first_pop_64_2[:,1], '.', label= 'initial population')
>>> axes[1,1].plot(first_col_moead_64_2, second_col_moead_64_2,'k*', label = 'moead')
>>> axes[1,1].plot(first_col_maco_64_2, second_col_maco_64_2,'ro', label = 'maco')
>>> axes[1,1].plot(first_col_nsga2_64_2, second_col_nsga2_64_2, 'b^', label = 'nsga2')
>>> axes[1,1].legend(loc='upper right')
>>> axes[1,1].set_title('ZDT3: final Pareto front (2nd run, pop=64)')
>>> axes[1,2].plot(first_pop_128_2[:,0], first_pop_128_2[:,1], '.', label= 'initial population')
>>> axes[1,2].plot(first_col_moead_128_2, second_col_moead_128_2,'k*', label = 'moead')
>>> axes[1,2].plot(first_col_maco_128_2, second_col_maco_128_2,'ro', label = 'maco')
>>> axes[1,2].plot(first_col_nsga2_128_2, second_col_nsga2_128_2, 'b^', label = 'nsga2')
>>> axes[1,2].legend(loc='upper right')
>>> axes[1,2].set_title('ZDT3: final Pareto front (2nd run, pop=128)')
>>> axes[2,0].plot(first_pop_32_3[:,0], first_pop_32_3[:,1], '.', label= 'initial population')
>>> axes[2,0].plot(first_col_moead_32_3, second_col_moead_32_3,'k*', label = 'moead')
>>> axes[2,0].plot(first_col_maco_32_3, second_col_maco_32_3,'ro', label = 'maco')
>>> axes[2,0].plot(first_col_nsga2_32_3, second_col_nsga2_32_3, 'b^', label = 'nsga2')
>>> axes[2,0].legend(loc='upper right')
>>> axes[2,0].set_title('ZDT3: final Pareto front (3rd run, pop=32)')
>>> axes[2,1].plot(first_pop_64_3[:,0], first_pop_64_3[:,1], '.', label= 'initial population')
>>> axes[2,1].plot(first_col_moead_64_3, second_col_moead_64_3,'k*', label = 'moead')
>>> axes[2,1].plot(first_col_maco_64_3, second_col_maco_64_3,'ro', label = 'maco')
>>> axes[2,1].plot(first_col_nsga2_64_3, second_col_nsga2_64_3, 'b^', label = 'nsga2')
>>> axes[2,1].legend(loc='upper right')
>>> axes[2,1].set_title('ZDT3: final Pareto front (3rd run, pop=64)')
>>> axes[2,2].plot(first_pop_128_3[:,0], first_pop_128_3[:,1], '.', label= 'initial population')
>>> axes[2,2].plot(first_col_moead_128_3, second_col_moead_128_3,'k*', label = 'moead')
>>> axes[2,2].plot(first_col_maco_128_3, second_col_maco_128_3,'ro', label = 'maco')
>>> axes[2,2].plot(first_col_nsga2_128_3, second_col_nsga2_128_3, 'b^', label = 'nsga2')
>>> axes[2,2].legend(loc='upper right')
>>> axes[2,2].set_title('ZDT3: final Pareto front (3rd run, pop=128)')
>>> for ax in axes.flat:
... ax.set(xlabel='f_1', ylabel='f_2')
... ax.grid()
结果图可以在下图中看到: