NLopt求解器使用初步教程#
在本教程中,我们展示了pygmo.nlopt的基本使用模式。这个用户定义的算法(UDA)封装了NLopt库,使其可以通过pygmo通用的pygmo.algorithm接口轻松访问。让我们看看这个奇迹是如何发生的。
我有梯度#
>>> import pygmo as pg
>>> uda = pg.nlopt("slsqp")
>>> algo = pg.algorithm(uda)
>>> print(algo)
Algorithm name: NLopt - slsqp: [deterministic]
C++ class name: ...
Thread safety: basic
Extra info:
NLopt version: ...
Solver: 'slsqp'
Last optimisation return code: NLOPT_SUCCESS (value = 1, Generic success return value)
Verbosity: 0
Individual selection policy: best
Individual replacement policy: best
Stopping criteria:
stopval: disabled
ftol_rel: disabled
ftol_abs: disabled
xtol_rel: 1e-08
xtol_abs: disabled
maxeval: disabled
maxtime: disabled
在几行代码中,我们构建了一个包含来自NLopt的"slsqp"求解器的pygmo.algorithm。有关通过NLopt库可用的求解器列表,请查看nlopt的文档。在本教程中,我们将使用"slsqp",这是一种适用于通用非线性规划问题(即非线性约束的单目标问题)的顺序二次规划算法。
NLopt库中使用的所有停止标准都可以通过专用属性获得,因此我们可以,例如,通过编写来设置ftol_rel:
>>> algo.extract(pg.nlopt).ftol_rel = 1e-8
让我们激活一些详细程度以存储日志并具有屏幕输出:
>>> algo.set_verbosity(1)
我们现在需要一个要解决的问题。让我们从pygmo中提供的一个UDP开始。pygmo.luksan_vlcek1问题是一个经典的、可扩展的、等式约束的问题。它也已经实现了梯度,所以我们暂时不用担心这个问题。
>>> udp = pg.luksan_vlcek1(dim = 20)
>>> prob = pg.problem(udp)
>>> pop = pg.population(prob, size = 1)
>>> pop.problem.c_tol = [1e-8] * prob.get_nc()
上面的行可以缩短,等同于:
>>> pop = pg.population(pg.luksan_vlcek1(dim = 20), size = 1)
>>> pop.problem.c_tol = [1e-8] * pop.problem.get_nc()
我们现在通过编写以下内容来解决这个问题:
>>> pop = algo.evolve(pop)
objevals: objval: violated: viol. norm:
1 250153 18 2619.51 i
2 132280 18 931.767 i
3 26355.2 18 357.548 i
4 14509 18 140.055 i
5 77119 18 378.603 i
6 9104.25 18 116.19 i
7 9104.25 18 116.19 i
8 2219.94 18 42.8747 i
9 947.637 18 16.7015 i
10 423.519 18 7.73746 i
11 82.8658 18 1.39111 i
12 34.2733 15 0.227267 i
13 11.9797 11 0.0309227 i
14 42.7256 7 0.27342 i
15 1.66949 11 0.042859 i
16 1.66949 11 0.042859 i
17 0.171358 7 0.00425765 i
18 0.00186583 5 0.000560166 i
19 1.89265e-06 3 4.14711e-06 i
20 1.28773e-09 0 0
21 7.45125e-14 0 0
22 3.61388e-18 0 0
23 1.16145e-23 0 0
Optimisation return status: NLOPT_XTOL_REACHED (value = 4, Optimization stopped because xtol_rel or xtol_abs was reached)
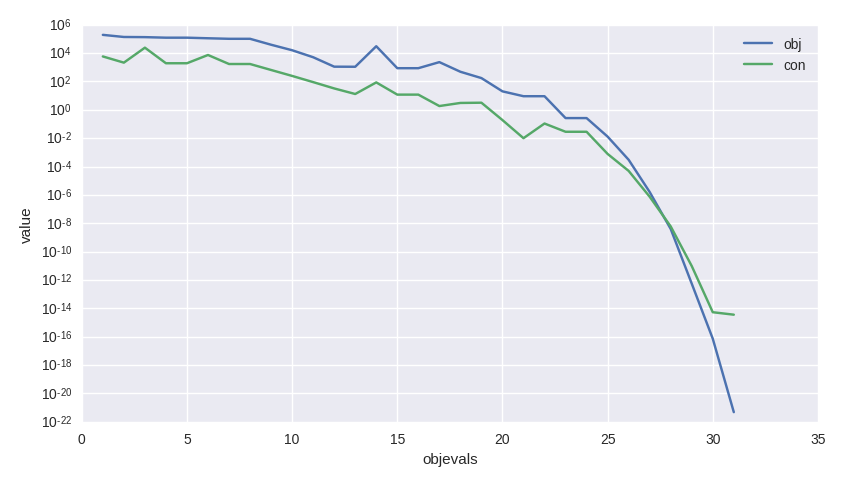
像往常一样,我们可以访问日志中的值来分析算法性能,例如,生成一个如图所示的图表。
>>> log = algo.extract(pg.nlopt).get_log()
>>> from matplotlib import pyplot as plt
>>> plt.semilogy([line[0] for line in log], [line[1] for line in log], label = "obj")
>>> plt.semilogy([line[0] for line in log], [line[3] for line in log], label = "con")
>>> plt.xlabel("objevals")
>>> plt.ylabel("value")
>>> plt.show()
我没有梯度#
上面的例子使用了一个UDP,pygmo.luksan_vlcek1,它还为目标和约束提供了显式梯度。
在许多情况下,用户可能匆忙编写的UDP或过于复杂以至于无法进行显式梯度计算。让我们看一个例子:
>>> class my_udp:
... def fitness(self, x):
... return (np.sin(x[0]+x[1]-x[2]), x[0] + np.cos(x[2]*x[1]), x[2])
... def get_bounds(self):
... return ([-1,-1,-1],[1,1,1])
... def get_nec(self):
... return 1
... def get_nic(self):
... return 1
>>> import numpy as np
>>> pop = pg.population(prob = my_udp(), size = 1)
>>> pop = algo.evolve(pop)
Traceback (most recent call last):
File "/home/dario/miniconda3/envs/pagmo/lib/python3.6/doctest.py", line 1330, in __run
compileflags, 1), test.globs)
File "<doctest default[3]>", line 1, in <module>
pop = algo.evolve(pop)
ValueError:
function: operator()
where: /home/user/Documents/pagmo2/include/pagmo/algorithms/nlopt.hpp, 259
what: during an optimization with the NLopt algorithm 'slsqp' a fitness gradient was requested, but the optimisation problem '<class 'my_udp'>' does not provide it
糟糕!我怎么可能为如此复杂的适应度表达式提供梯度呢?显然在这里求导是不可行的 :)
幸运的是,pygmo 提供了一些工具来执行数值微分。特别是 pygmo.estimate_gradient() 和 pygmo.estimate_gradient_h()
可以非常直接地使用。两者之间的区别在于用于数值估计梯度的有限差分公式,小写的 _h
代表高保真(使用了一个精确到六阶的公式:参见文档)。所以我们需要做的就是在我们的 UDP 中提供梯度:
>>> class my_udp:
... def fitness(self, x):
... return (np.sin(x[0]+x[1]-x[2]), x[0] + np.cos(x[2]*x[1]), x[2])
... def get_bounds(self):
... return ([-1,-1,-1],[1,1,1])
... def get_nec(self):
... return 1
... def get_nic(self):
... return 1
... def gradient(self, x):
... return pg.estimate_gradient_h(lambda x: self.fitness(x), x)
>>> pop = pg.population(prob = my_udp(), size = 1)
>>> pop = algo.evolve(pop)
fevals: fitness: violated: viol. norm:
1 0.694978 2 1.92759 i
2 -0.97723 1 9.87066e-05 i
3 -0.999189 1 0.00295056 i
4 -1 1 3.2815e-05 i
5 -1 1 1.11149e-08 i
6 -1 1 8.12683e-14 i
7 -1 0 0
让我们评估一下这种优化在调用各种函数方面的成本:
>>> pop.problem.get_fevals()
23
>>> pop.problem.get_gevals()
21
pygmo.problem.fitness() 被调用了总共23次,而 pygmo.problem.gradient() 被调用了总共21次。由于我们使用
pygmo.estimate_gradient_h() 来数值提供梯度,每次调用 pygmo.problem.gradient()
会导致6次对 my_udp.fitness() 的评估。因此,最终总共进行了23 + 6 * 21次对 my_udp.fitness() 的调用。