解决20维Schwefel问题

在本教程中，我们将使用许多不同的算法来解决20维的Schwefel问题。这样的UDP在类schwefel中编码。脚本的结果是右侧的图表，该图表将在几秒钟内生成，并报告了25次运行中一些默认实例的pygmo求解器的平均值。其余的图表展示了两组最成功算法的一些单次重复。

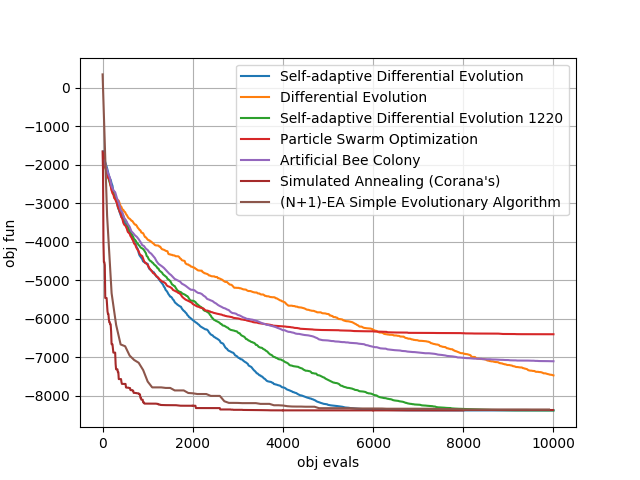
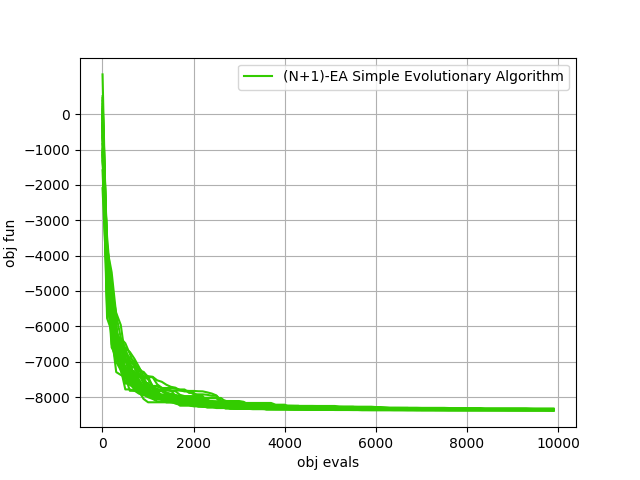
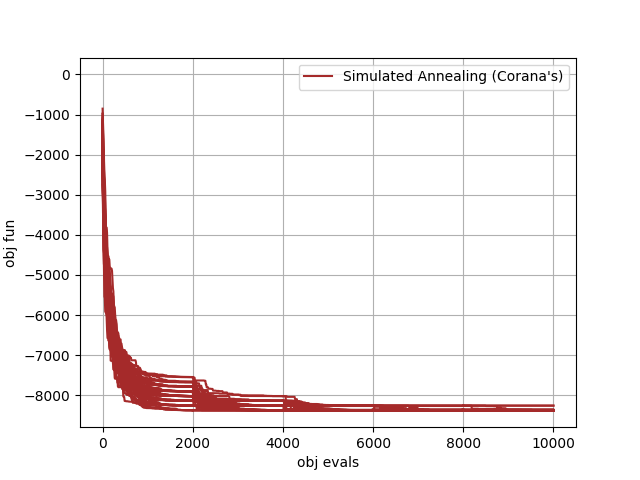
>>> import pygmo as pg
>>> # The user-defined problem
>>> udp = pg.schwefel(dim = 20)
>>> # The pygmo problem
>>> prob = pg.problem(udp)

>>> # For a number of generation based algorithms we can use a similar script to run and average over 25 runs.
>>> udas = [pg.sade(gen=500), pg.de(gen=500), pg.de1220(gen=500), pg.pso(gen=500), pg.bee_colony(gen=250, limit=20)]
>>> for uda in udas: 
...     logs = []
...     for i in range(25):
...         algo = pg.algorithm(uda)
...         algo.set_verbosity(1) # regulates both screen and log verbosity
...         pop = pg.population(prob, 20)
...         pop = algo.evolve(pop)
...         logs.append(algo.extract(type(uda)).get_log())
...     logs = np.array(logs)
...     avg_log = np.average(logs,0)
...     plt.plot(avg_log[:,1],avg_log[:,2]-418.9829*20 , label=algo.get_name())

>>> # For simulated annealing, since we will be using some reannealing we have to code a different script (and we will
>>> # also not take any average for brevity)
>>> logs = []
>>> algo = pg.algorithm(pg.simulated_annealing(10, 0.01, 5))
>>> algo.set_verbosity(10)
>>> pop = pg.population(prob, 20)
>>> for i in range(5): 
...     pop = algo.evolve(pop)
...     logs.append(algo.extract(pg.simulated_annealing).get_log())
>>> for i in range(5): 
...      plt.plot([l[0]+2000*i for l in logs[i]],[l[1]-418.9829*20 for l in logs[i]],"brown")
>>> plt.plot([0,0],[1,1],"brown", label=algo.get_name()) 

>>> # For the simple evolutionary startegy we also need ad hoc code
>>> logs = []
>>> algo = pg.algorithm(pg.sea(gen = 10000))
>>> algo.set_verbosity(100)
>>> pop = pg.population(prob, 1)
>>> pop = algo.evolve(pop) 
>>> logs = algo.extract(pg.sea).get_log() 
>>> plt.plot([l[1] for l in logs],[l[2]-418.9829*20 for l in logs], label = algo.get_name()) 

>>> # We then add details to the plot
>>> plt.legend() 
>>> plt.yticks([-8000,-7000,-6000,-5000,-4000,-3000,-2000,-1000,0]) 
>>> plt.grid()