参与CEC2013竞赛#

在本教程中，我们将展示如何使用pygmo在2013年6月21日至23日墨西哥坎昆CEC-2013上用于真实参数单目标优化的特别会议和竞赛中使用的测试问题套件上运行算法。

所有的CEC 2013问题都是盒约束的、连续的、单目标问题，并且由pygmo在类cec2013中作为UDP（用户定义问题）提供。实例化其中一个问题很简单：

>>> import pygmo as pg
>>> # The user-defined problem
>>> udp = pg.cec2013(prob_id = 24, dim = 10)
>>> # The pygmo problem
>>> prob = pg.problem(udp)

像往常一样，我们可以通过将其打印到屏幕上来快速检查问题：

>>> print(prob) 
Problem name: CEC2013 - f24(cf04)
    C++ class name: ...

    Global dimension:                       10
    Integer dimension:                      0
    Fitness dimension:                      1
    Number of objectives:                   1
    Equality constraints dimension:         0
    Inequality constraints dimension:       0
    Lower bounds: [-100, -100, -100, -100, -100, ... ]
    Upper bounds: [100, 100, 100, 100, 100, ... ]
    Has batch fitness evaluation: false

    Has gradient: false
    User implemented gradient sparsity: false
    Has hessians: false
    User implemented hessians sparsity: false

    Fitness evaluations: 0

    Thread safety: basic

让我们假设我们想要评估（比如说）优化算法 cmaes（它实现了用户定义的协方差矩阵适应进化策略）在整个 cec2013 问题集上在维度 D=2 时的表现。由于比赛规则允许 D * 10000 次适应度评估，我们选择种群大小为 50 和 400 代：

CEC2013-JDE-2D CEC2013-CMAES-2D CEC2013-SIMANNEAL-2D CEC2013-PSO-2D 
>>> # The cmaes pygmo algorithm
>>> algo = pg.algorithm(pg.cmaes(gen=1000, ftol=1e-9, xtol=1e-9))
>>> # Defining all 28 problems dimension
>>> D = 2
>>> # Running the algo on them multiple times
>>> error = []
>>> trials = 25
>>> for j in range(trials): 
...         for i in range(28):
...                 prob = pg.problem(pg.cec2013(prob_id = i+1, dim = D))
...                 pop = pg.population(prob,50)
...                 pop = algo.evolve(pop)
...                 error.append(pop.get_f()[pop.best_idx()][0] + 1400 - 100*i - 100*(i>13))

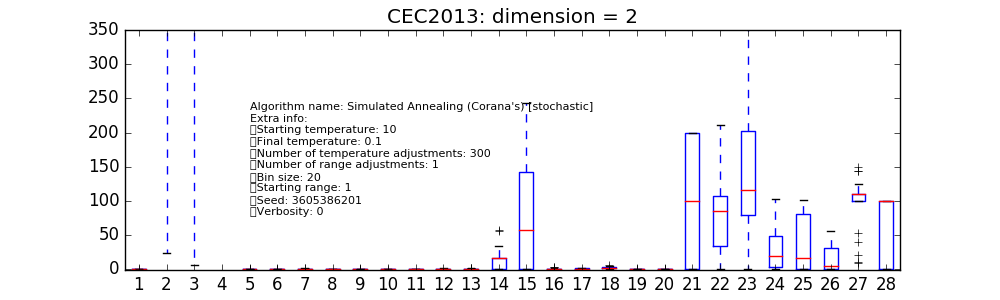
在脚本的最后，可以轻松生成一个matplotlib箱线图，报告28个问题实例中每个实例的结果：

>>> import matplotlib.pyplot as plt 
>>> res = plt.boxplot([error[s::28] for s in range(28)]) 
>>> plt.text(5, 80, algo.__repr__(), fontsize=8) 
>>> fig = plt.gcf() 
>>> fig.set_size_inches(10,3, forward=True) 
>>> plt.ylim([-1,350]) 
>>> plt.title("CEC2013: dimension = 2") 
>>> plt.show()

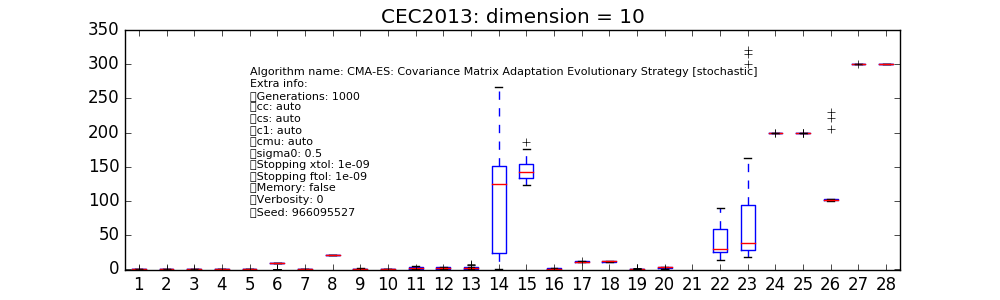
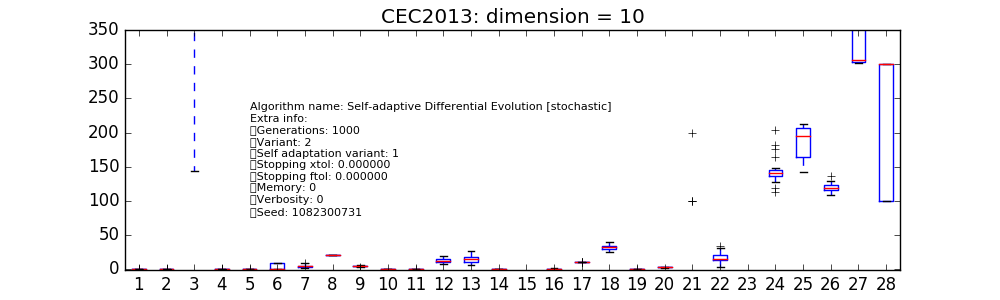
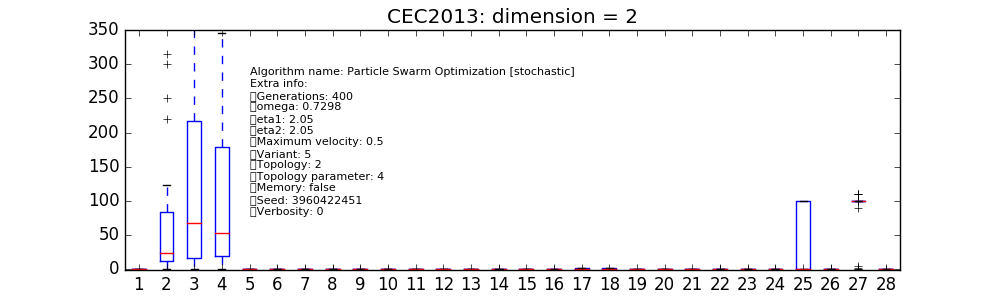
同样的方法也可以应用于不同的用户定义算法。在右侧的各种图表中，我们仅报告了pygmo核心中可用的少数几种。在这个低维度下，可以看到为cmaes和sade（jDE）选择的特定实例表现特别好。这里需要注意的是，cmaes的结果通常花费的适应度评估预算少于可用预算，因此在这些低维度下进行适当的比较应允许重新启动，以充分利用允许的预算。

上述脚本可以再次运行以处理更高维度的问题，例如，在D = 10时，并使用更大的种群规模以适应更大的适应度评估预算，对于选定的cmaes和sade实例，可以获得以下图表：

CEC2013-CMAES-10D CEC2013-JDE-10D