高级超体积计算与分析#
在本教程中,我们将介绍关于超体积指标的更高级主题,并评论其在pygmo中的预期计算性能。
使用特定算法计算超体积#
pygmo 使用不同的算法来计算超体积指标和超体积贡献。 默认情况下,它会选择相对于给定点集的维度预期能产生最快计算的算法。 可以通过显式传递算法作为相应方法的参数来绕过此选择:
>>> import pygmo as pg
>>> hv = pg.hypervolume([[1,0,1],[1,1,0],[-1,2,2]])
>>> hv.compute([5,5,5], hv_algo=pg.hvwfg())
114.0
上面的代码将使用Walking Fish Group算法计算超体积指标,而
>>> hv.compute([5,5,5])
114.0
将默认使用hv3d算法,因为pygmo预期它在三维情况下会更快。以下算法在pygmo中可用:
注意
某些算法可能不提供某些功能,例如:bf_fpras 算法专为高效近似高维超体积而设计,仅支持“compute”方法。
我们将在教程近似超体积中讨论近似超体积的细节。在本教程中,我们只关注精确方法。
pygmo超体积计算的运行时分析#

我们已经实现了一系列算法,供需要计算超体积时选择。
我们利用这一事实为用户提供了一个高效的计算引擎,该引擎在默认情况下很可能会选择最快的算法。在一些实验过程中,我们测量了我们的引擎对于具有不同Front size(点数)和Dimension的前沿的能力。
注意
获得的结果特定于执行这些实验的计算机的硬件和架构。本教程及后续教程中图表的主要思想是展示不同Front size和Dimension设置下执行时间的相对缩放。
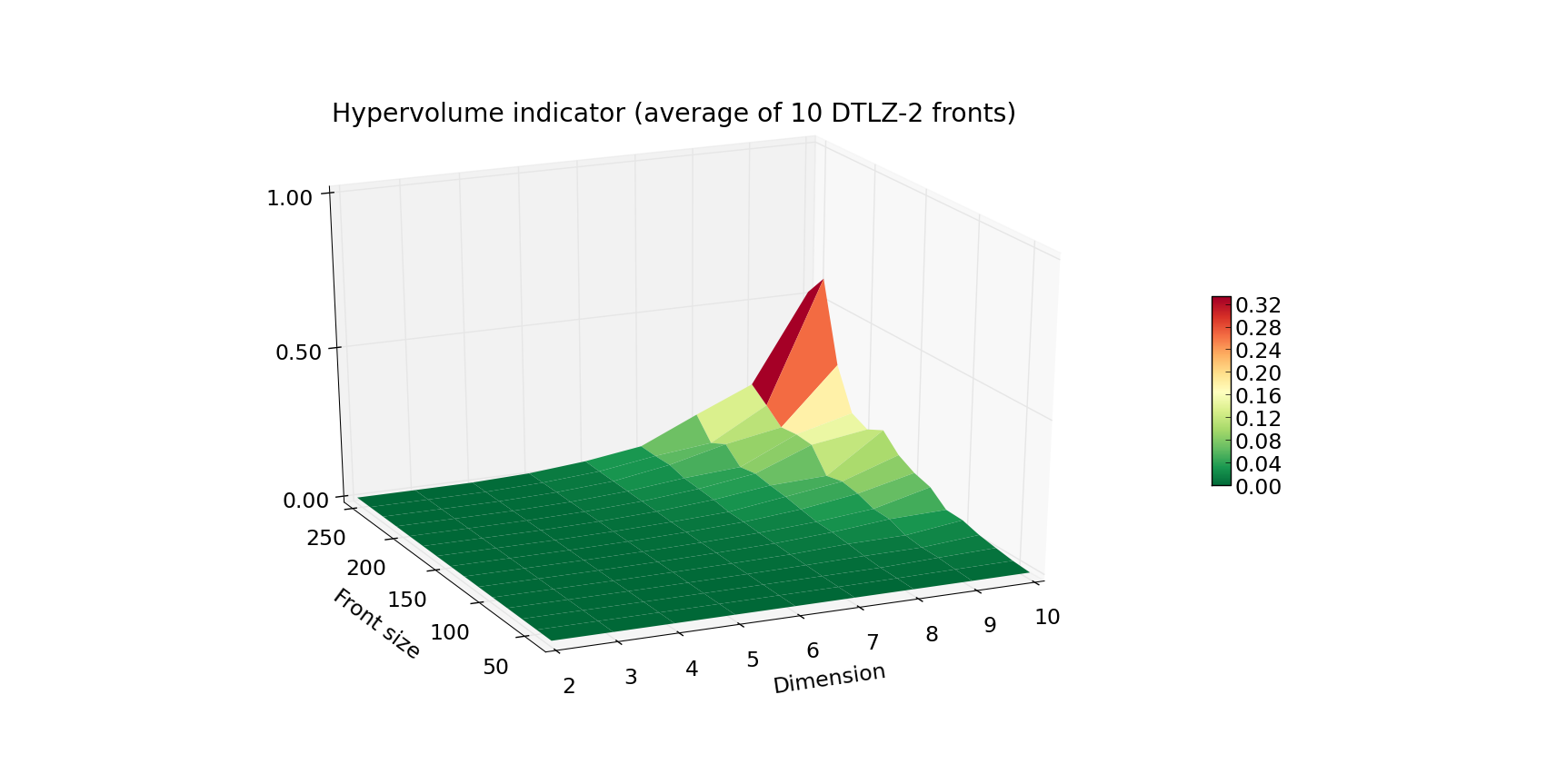
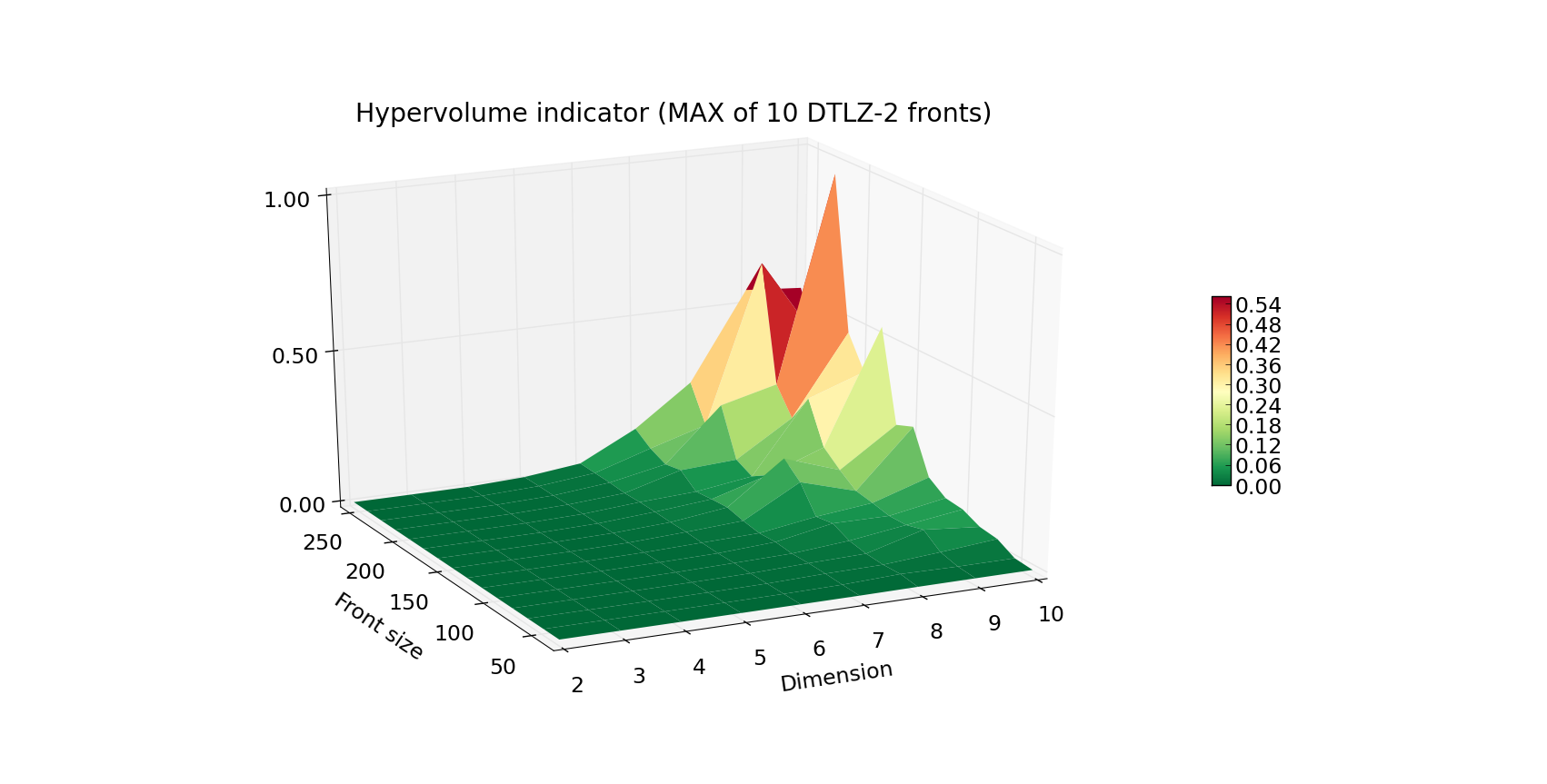
结果显示在右侧的图表中。
上面的第一个图显示了计算DTLZ-2问题前沿的运行时间(每个给定的Front size和Dimension组合的10次前沿的平均值)。下面的图显示了最坏情况(给定Front size和Dimension的10次运行中的最大时间)。Z轴和颜色表示执行时间(以秒为单位)。正如你所看到的,计算100个点及以下的超体积相当快,即使面对10维问题也是如此。当你设计自己的实验时,请注意超体积算法的最坏情况复杂度是指数级的。
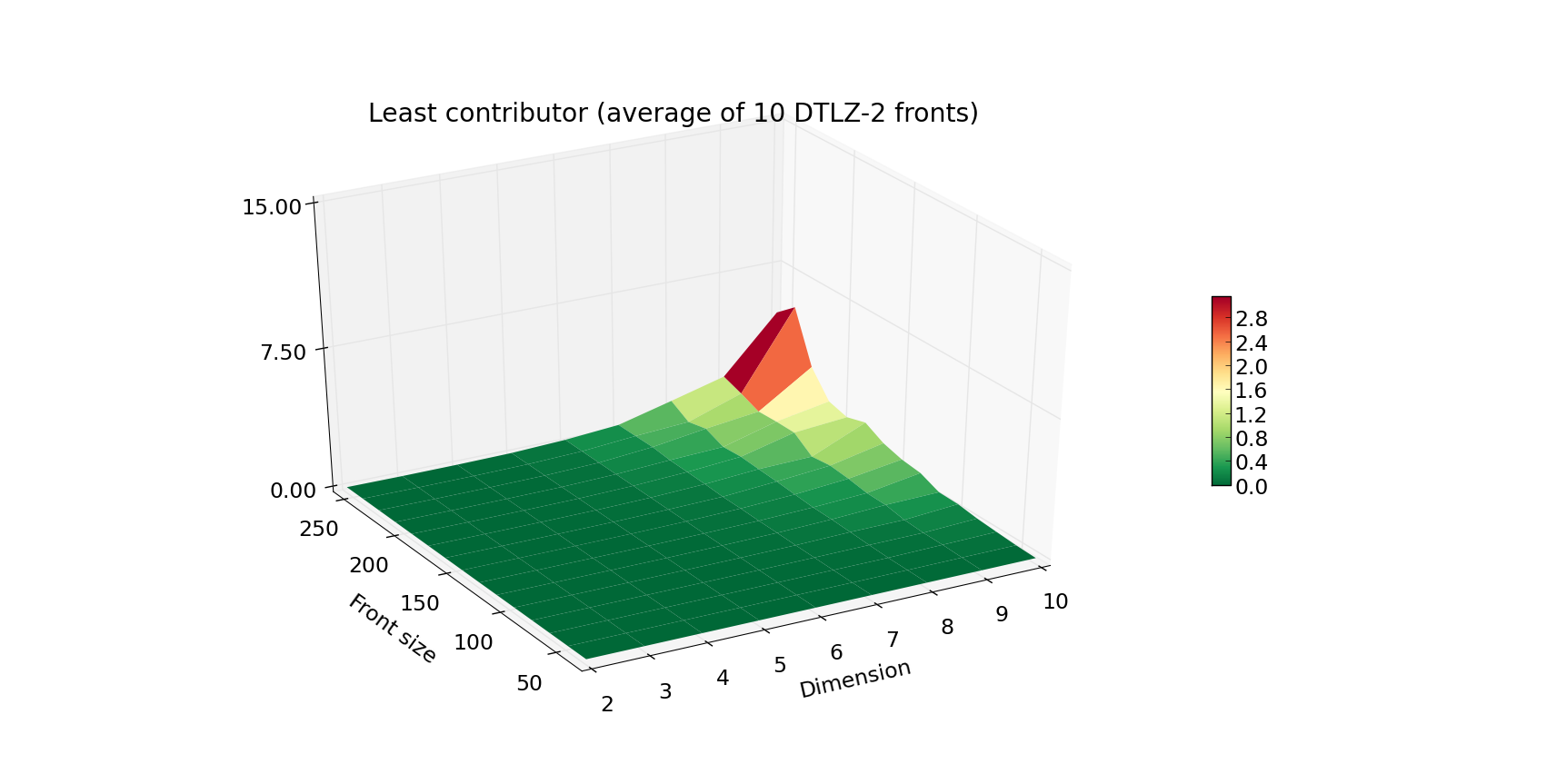
尽管超体积指标是帕累托前沿的一个非常常见的质量指标,许多多目标优化器需要一个稍微不同的指标来评估种群中给定个体的质量。这通过计算给定个体对种群的独占贡献来解决,在大多数情况下,归结为消除贡献最少的个体。因此,我们还将报告least_contributor方法的时间。
执行时间的增加以类似的方式进展,但Z轴现在按10倍的比例缩放。
算法比较#
在本节中,我们将快速比较可用的算法,以支持我们对默认算法集的选择。由于在许多情况下,多目标问题要么是二维的,要么是三维的,因此为每种情况专门设计一个算法非常重要。目前,PyGMO中有三种精确算法,其中两种专门针对特定维度:
尽管WFG被认为是超体积计算的最先进算法之一,但针对2维和3维的专用算法在运行时间方面表现优于通用算法,如下图所示,其中hv3d算法显示出相对于WFG更低的复杂度。

算法简短摘要#
如果未另行指定,pygmo 使用的默认算法将是:
超体积方法 |
二维 |
3D |
4D及以上 |
|---|---|---|---|
|
|||
|
特定算法支持的方法如下:
hv_algorithm |
计算 |
独家 |
最小贡献者 |
最大贡献者 |
贡献 |
|---|---|---|---|---|---|
是的 |
是的 |
是的 |
是 |
是的 |
|
是的 |
是的 |
是的 |
是的 |
是的 |
|
是的 |
是的 |
是的 |
是的 |
是的 |
|
否 |
否 |
是的 |
是的 |
否 |
|
是的 |
否 |
否 |
否 |
否 |