贝叶斯非参数因果推断#
import arviz as az
import matplotlib.lines as mlines
import matplotlib.patches as mpatches
import matplotlib.pyplot as plt
import networkx as nx
import numpy as np
import pandas as pd
import pymc as pm
import pymc_bart as pmb
import pytensor.tensor as pt
import statsmodels.api as sm
import xarray as xr
from sklearn.ensemble import GradientBoostingRegressor, RandomForestRegressor
%config InlineBackend.figure_format = 'retina' # high resolution figures
az.style.use("arviz-darkgrid")
rng = np.random.default_rng(42)
因果推断和倾向评分#
没有什么主张比因果关系的断言更强烈,也没有什么主张比它更具有争议性。一个天真的世界模型——充满了脆弱的联系和非逻辑的推论,是阴谋论和愚蠢的特征。另一方面,对因果关系的精炼和详细的理解,以清晰的预期、合理的联系和有力的反事实为特征,将引导你顺利通过这个喧嚣、纷繁复杂的世界。
在实验环境中,因果推断与观察环境中的因果推断有所不同。在实验环境中,治疗是随机分配的。而对于观察数据,我们永远不知道将每个分析对象分配到其治疗组的机制。这可能导致由于选择效应混淆了治疗分析而产生偏差。倾向评分是研究人群中每个个体接受治疗状态(例如吸烟者/非吸烟者、离婚/已婚)的估计概率。下面我们将回顾理解个体治疗倾向如何有助于减轻这种选择偏差。
非参数方法用于估计倾向评分和治疗效果,旨在保持对精确函数关系的不可知论,并避免模型错误指定。这一推动源于这样一种观点:过多的建模假设会培养出不利于混杂错误的环境,应予以避免。参见《不可知统计学基础》 Aronow 和 Miller [2019]。我们最终将论证,这种极简主义的“沙漠景观”美学在面对具有实际意义的因果问题时会破碎,因为在这种情况下,即使我们可以利用非参数方法,也需要实质性的假设。
在本笔记本中,我们将解释并论证在因果推断问题分析中使用倾向评分的原因。我们的重点将放在我们(a)如何估计倾向评分以及(b)在因果问题分析中如何使用它们。我们将看到它们如何帮助避免因果推断中的选择偏差风险以及它们可能出错的地方。这种方法应该适合熟悉加权和使用先验信息重新加权的贝叶斯分析师。倾向评分加权只是另一种机会,通过关于世界的知识来丰富您的模型。我们将展示它们如何直接应用,然后在去偏机器学习方法的因果推断背景下间接应用。
我们将使用两个数据集来说明这些模式:《因果推断:何为因果》Hernán 和 Robins [2020]中使用的NHEFS数据,以及在《贝叶斯非参数因果推断与缺失数据》Daniels 等人 [2024]中分析的第二个以患者为中心的数据集。我们将重点强调非参数BART模型与简单回归模型在倾向评分和因果效应估计方面的对比。
关于倾向评分匹配的注意事项
倾向评分通常与倾向评分匹配技术同义。我们不会涉及这个主题。它是倾向评分建模的自然延伸,但在我们看来,它通过以下要求引入了复杂性:(a) 选择匹配算法和 (b) 由于样本量减少而带来的信息损失。
演示文稿的结构#
下面我们将看到一些非参数方法用于因果效应估计的示例。其中一些方法效果良好,而另一些则会误导我们。我们将展示这些方法如何作为工具,在我们的推断框架中施加越来越严格的假设。在整个过程中,我们将使用潜在结果表示法来讨论因果推断——我们大量借鉴了Aronow和Miller [2019]的工作,可以参考以获取更多详细信息。但非常简要地说,当我们想要讨论治疗状态对结果\(Y\)的因果影响时,我们将结果\(Y(t)\)表示为在治疗方案\(T = t\)下的结果度量\(Y\)。
倾向评分在选择效应偏差中的应用
NHEFS 数据关于体重减轻与吸烟的关系
倾向评分在选择效应偏差中的应用
健康支出数据及其与吸烟的关系
应用Debiased/Double ML估计ATE
应用中介分析来估计直接和间接效应
这些不断升级的假设集,在不同混杂威胁下为因果推断提供了依据,从而揭示了整个推断过程。
为什么我们要关注倾向评分?#
通过观察数据,我们无法重新运行分配机制,但我们可以估计它,并将我们的数据转换为按比例加权每个组内的数据摘要,以便分析受到每个组中不同阶层过度代表的影响较小。这就是我们希望使用倾向评分来实现的目标。
首先,从某种表面上看,倾向评分是一种降维技术。我们将一个复杂的协变量配置文件 \(X_{i}\) 表示个体的测量属性,并将其简化为一个标量 \(p^{i}_{T}(X)\)。它也是一种工具,用于思考个体在不同治疗方案下的潜在结果。在政策评估的背景下,它可以帮助部分消除政策采纳在人口各阶层中的激励程度。是什么推动了人口各细分市场的采纳或分配?如何引导不同的人口阶层趋向或远离政策的采纳?理解这些动态对于评估为何在任何样本数据中可能出现选择偏差至关重要。Paul Goldsmith-Pinkham 的 讲座 特别清楚地解释了这一点,以及为什么这种观点对结构计量经济学家具有吸引力。
在思考倾向评分时,关键的想法是:我们不能授权因果声明,除非(i)处理分配与协变量配置文件无关,即 \(T \perp\!\!\!\perp X\) 和(ii)结果 \(Y(0)\) 和 \(Y(1)\) 同样在给定处理 \(T | X\) 的条件下独立。如果这些条件成立,那么我们说在给定 \(X\) 的情况下,\(T\) 是 强可忽略的。这也偶尔被称为 无混杂性 或 可交换性 假设。对于由协变量配置文件 \(X\) 定义的每个群体层,我们要求在控制 \(X\) 后,个体采用哪种处理状态几乎是随机的。这意味着在控制 \(X\) 后,处理组和未处理组之间的任何结果差异都可以归因于处理本身,而不是混杂变量。
这是一个定理,如果\(T\)在给定\(X\)的情况下是强可忽略的,那么在给定\(p_{T}(X)\)的情况下,(i)和(ii)也成立。因此,有效的统计推断可以在较低维的空间中进行,使用倾向得分作为高维数据的代理。这是有用的,因为复杂协变量剖面的某些层可能人口稀少,因此用倾向得分替代可以避免高维缺失数据的风险。当我们已经控制了足够多的政策采纳驱动因素时,因果推断是无偏的,每个协变量剖面\(X\)内的选择效应似乎基本上是随机的。这一见解表明,当你想要估计因果效应时,你只需要控制影响治疗分配概率的协变量。更具体地说,如果建模分配机制比建模结果机制更容易,那么在因果推断的情况下,可以用观察到的数据替代。
假设我们正在测量正确的协变量分布以实现强可忽略性,那么倾向评分可以被谨慎地用于支持因果推断。
倾向得分图解#
一些方法学家主张通过假设和评估有向无环图来分析因果主张,这些图据称代表了因果影响的关系。在倾向评分分析的情况下,我们有以下图片。注意X对结果的影响如何不变,但它对治疗的影响被捆绑到倾向评分指标中。我们对强可忽略性的假设正在为我们提供因果主张的许可。倾向评分方法通过纠正使用捆绑在倾向评分中的结构来实现这些移动。
Show code cell source
fig, axs = plt.subplots(1, 2, figsize=(20, 15))
axs = axs.flatten()
graph = nx.DiGraph()
graph.add_node("X")
graph.add_node("p(X)")
graph.add_node("T")
graph.add_node("Y")
graph.add_edges_from([("X", "p(X)"), ("p(X)", "T"), ("T", "Y"), ("X", "Y")])
graph1 = nx.DiGraph()
graph1.add_node("X")
graph1.add_node("T")
graph1.add_node("Y")
graph1.add_edges_from([("X", "T"), ("T", "Y"), ("X", "Y")])
nx.draw(
graph,
arrows=True,
with_labels=True,
pos={"X": (1, 2), "p(X)": (1, 3), "T": (1, 4), "Y": (2, 1)},
ax=axs[1],
node_size=6000,
font_color="whitesmoke",
font_size=20,
)
nx.draw(
graph1,
arrows=True,
with_labels=True,
pos={"X": (1, 2), "T": (1, 4), "Y": (2, 1)},
ax=axs[0],
node_size=6000,
font_color="whitesmoke",
font_size=20,
)
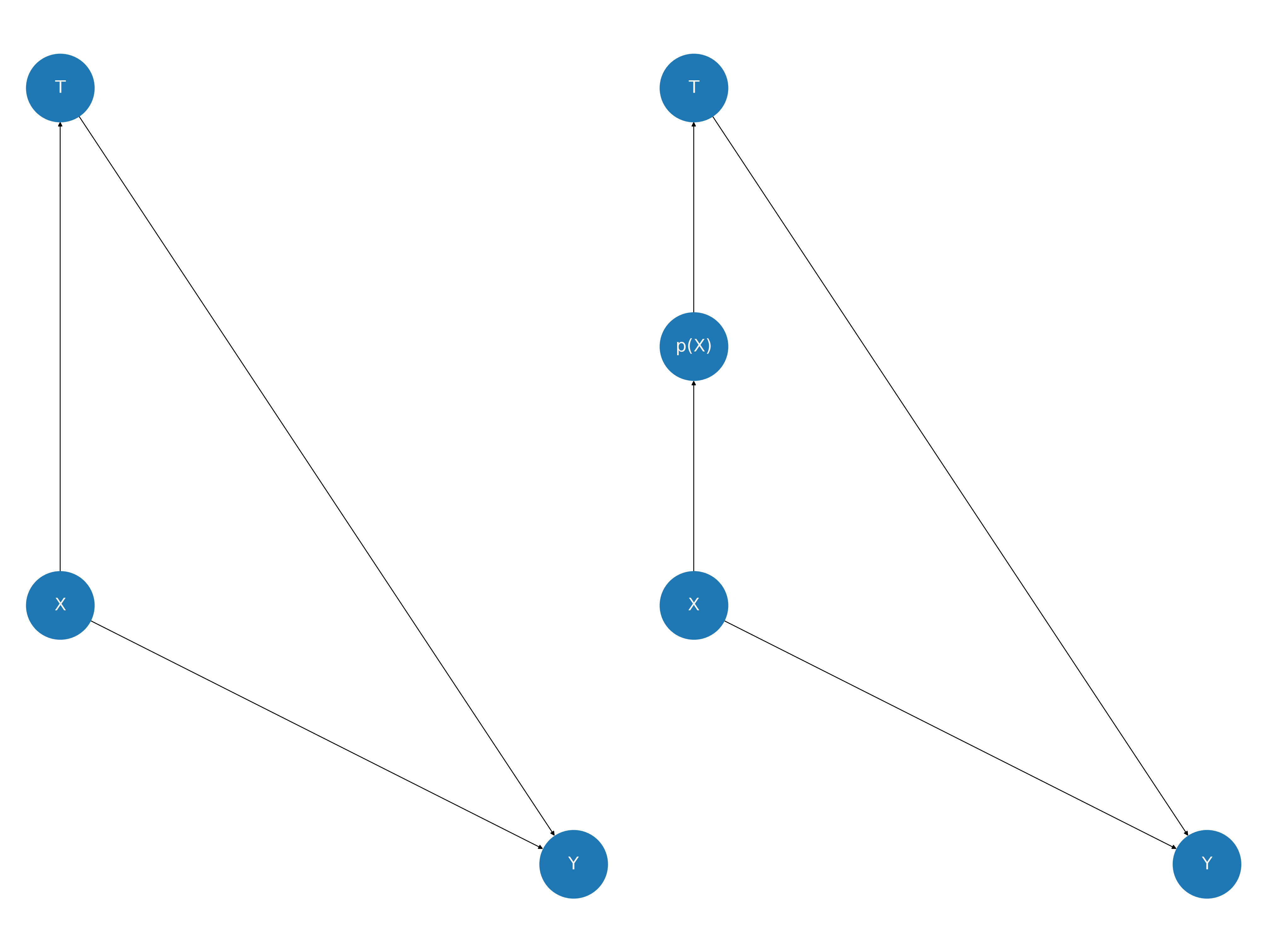
在上图中,我们看到如何通过包含倾向评分变量来阻断协变量剖面X与处理变量T之间的路径。 这是一个关于强可忽略性假设的有用视角,因为它意味着\(T \perp\!\!\!\perp X |p(X)\),这表明在给定倾向评分的情况下,协变量剖面在处理分支之间是平衡的。这是所假设设计的可检验含义!
如果我们的处理状态是这样的,即个体或多或少会主动选择自己进入该状态,那么对处理组和对照组之间的差异进行简单的比较将会产生误导,因为我们可能在总体中过度代表了某些类型的个体(协变量配置文件)。随机化通过平衡处理组和对照组之间的协变量配置文件,并确保结果与处理分配无关来解决这个问题。但我们不能总是进行随机化。倾向评分是有用的,因为它们可以通过对观测数据进行特定的转换,在样本数据中模拟如同随机分配处理状态的效果。
这种基于倾向评分的假设和随后的平衡测试通常被用来替代对系统决定处理分配的结构DAG的详细阐述。其理念是,如果我们能够在给定倾向评分的情况下实现协变量的平衡,我们就可以模拟一种随机分配,从而避免指定过多结构的麻烦,并对机制的结构保持不可知论。这通常是一种有用的策略,但正如我们将看到的,它忽略了因果问题的特异性和数据生成过程。
非混杂推断:NHEFS数据#
来自国家健康和营养调查的数据集记录了大约1500人在两个时期的体重、活动和吸烟习惯的详细信息。第一个时期建立了基线,并在10年后的随访期进行了跟踪。我们将分析个体(trt == 1)是否在随访访问前戒烟。每个个体的outcome表示比较两个时期的相对体重增减。
try:
nhefs_df = pd.read_csv("../data/nhefs.csv")
except:
nhefs_df = pd.read_csv(pm.get_data("nhefs.csv"))
nhefs_df.head()
| age | race | sex | smokeintensity | smokeyrs | wt71 | active_1 | active_2 | education_2 | education_3 | education_4 | education_5 | exercise_1 | exercise_2 | age^2 | wt71^2 | smokeintensity^2 | smokeyrs^2 | trt | outcome | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 0 | 42 | 1 | 0 | 30 | 29 | 79.04 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 1764 | 6247.3216 | 900 | 841 | 0 | -10.093960 |
| 1 | 36 | 0 | 0 | 20 | 24 | 58.63 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 1296 | 3437.4769 | 400 | 576 | 0 | 2.604970 |
| 2 | 56 | 1 | 1 | 20 | 26 | 56.81 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 1 | 3136 | 3227.3761 | 400 | 676 | 0 | 9.414486 |
| 3 | 68 | 1 | 0 | 3 | 53 | 59.42 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 4624 | 3530.7364 | 9 | 2809 | 0 | 4.990117 |
| 4 | 40 | 0 | 0 | 20 | 19 | 87.09 | 1 | 0 | 1 | 0 | 0 | 0 | 1 | 0 | 1600 | 7584.6681 | 400 | 361 | 0 | 4.989251 |
我们可能会想知道调查回复中代表了哪些人,以及在这个调查中测量的差异在多大程度上对应于更广泛人群中的模式?如果我们看一下结果中的总体差异:
raw_diff = nhefs_df.groupby("trt")[["outcome"]].mean()
print("Treatment Diff:", raw_diff["outcome"].iloc[1] - raw_diff["outcome"].iloc[0])
raw_diff
Treatment Diff: 2.540581454955888
| outcome | |
|---|---|
| trt | |
| 0 | 1.984498 |
| 1 | 4.525079 |
我们发现两个组之间存在一些总体差异,但进一步细分后,我们可能会担心这些差异是由于处理组和对照组在不同协变量分布上的不平衡造成的。也就是说,我们可以检查数据在不同层级上的隐含差异,以发现我们可能在不同人群细分中存在不平衡。这种不平衡表明了进入处理状态的一些选择效应,这是我们希望通过倾向评分建模来解决的问题。
strata_df = (
nhefs_df.groupby(
[
"trt",
"sex",
"race",
"active_1",
"active_2",
"education_2",
]
)[["outcome"]]
.agg(["count", "mean"])
.rename({"age": "count"}, axis=1)
)
global_avg = nhefs_df["outcome"].mean()
strata_df["global_avg"] = global_avg
strata_df["diff"] = strata_df[("outcome", "mean")] - strata_df["global_avg"]
strata_df.reset_index(inplace=True)
strata_df.columns = [" ".join(col).strip() for col in strata_df.columns.values]
strata_df.style.background_gradient(axis=0)
| trt | sex | race | active_1 | active_2 | education_2 | outcome count | outcome mean | global_avg | diff | |
|---|---|---|---|---|---|---|---|---|---|---|
| 0 | 0 | 0 | 0 | 0 | 0 | 0 | 193 | 2.858158 | 2.638300 | 0.219859 |
| 1 | 0 | 0 | 0 | 0 | 0 | 1 | 46 | 3.870131 | 2.638300 | 1.231831 |
| 2 | 0 | 0 | 0 | 0 | 1 | 0 | 29 | 4.095394 | 2.638300 | 1.457095 |
| 3 | 0 | 0 | 0 | 0 | 1 | 1 | 5 | 0.568137 | 2.638300 | -2.070163 |
| 4 | 0 | 0 | 0 | 1 | 0 | 0 | 160 | 0.709439 | 2.638300 | -1.928861 |
| 5 | 0 | 0 | 0 | 1 | 0 | 1 | 36 | 0.994271 | 2.638300 | -1.644029 |
| 6 | 0 | 0 | 1 | 0 | 0 | 0 | 36 | 2.888559 | 2.638300 | 0.250259 |
| 7 | 0 | 0 | 1 | 0 | 0 | 1 | 4 | 6.322334 | 2.638300 | 3.684034 |
| 8 | 0 | 0 | 1 | 0 | 1 | 0 | 4 | -5.501240 | 2.638300 | -8.139540 |
| 9 | 0 | 0 | 1 | 1 | 0 | 0 | 20 | -1.354505 | 2.638300 | -3.992804 |
| 10 | 0 | 0 | 1 | 1 | 0 | 1 | 9 | 0.442138 | 2.638300 | -2.196162 |
| 11 | 0 | 1 | 0 | 0 | 0 | 0 | 157 | 2.732690 | 2.638300 | 0.094390 |
| 12 | 0 | 1 | 0 | 0 | 0 | 1 | 59 | 2.222754 | 2.638300 | -0.415546 |
| 13 | 0 | 1 | 0 | 0 | 1 | 0 | 36 | 2.977257 | 2.638300 | 0.338957 |
| 14 | 0 | 1 | 0 | 0 | 1 | 1 | 17 | 2.087297 | 2.638300 | -0.551003 |
| 15 | 0 | 1 | 0 | 1 | 0 | 0 | 200 | 1.700405 | 2.638300 | -0.937895 |
| 16 | 0 | 1 | 0 | 1 | 0 | 1 | 55 | -0.492455 | 2.638300 | -3.130754 |
| 17 | 0 | 1 | 1 | 0 | 0 | 0 | 19 | 2.644629 | 2.638300 | 0.006329 |
| 18 | 0 | 1 | 1 | 0 | 0 | 1 | 18 | 3.047791 | 2.638300 | 0.409491 |
| 19 | 0 | 1 | 1 | 0 | 1 | 0 | 9 | 1.637378 | 2.638300 | -1.000922 |
| 20 | 0 | 1 | 1 | 0 | 1 | 1 | 4 | 0.735846 | 2.638300 | -1.902454 |
| 21 | 0 | 1 | 1 | 1 | 0 | 0 | 34 | 0.647564 | 2.638300 | -1.990736 |
| 22 | 0 | 1 | 1 | 1 | 0 | 1 | 13 | 4.815856 | 2.638300 | 2.177556 |
| 23 | 1 | 0 | 0 | 0 | 0 | 0 | 76 | 4.737206 | 2.638300 | 2.098906 |
| 24 | 1 | 0 | 0 | 0 | 0 | 1 | 18 | 5.242349 | 2.638300 | 2.604049 |
| 25 | 1 | 0 | 0 | 0 | 1 | 0 | 23 | 3.205170 | 2.638300 | 0.566870 |
| 26 | 1 | 0 | 0 | 0 | 1 | 1 | 4 | 6.067620 | 2.638300 | 3.429320 |
| 27 | 1 | 0 | 0 | 1 | 0 | 0 | 70 | 4.630845 | 2.638300 | 1.992545 |
| 28 | 1 | 0 | 0 | 1 | 0 | 1 | 12 | 7.570608 | 2.638300 | 4.932308 |
| 29 | 1 | 0 | 1 | 0 | 0 | 0 | 4 | 7.201967 | 2.638300 | 4.563668 |
| 30 | 1 | 0 | 1 | 0 | 0 | 1 | 3 | 10.698826 | 2.638300 | 8.060526 |
| 31 | 1 | 0 | 1 | 1 | 0 | 0 | 7 | 0.778359 | 2.638300 | -1.859941 |
| 32 | 1 | 0 | 1 | 1 | 0 | 1 | 3 | 9.790449 | 2.638300 | 7.152149 |
| 33 | 1 | 1 | 0 | 0 | 0 | 0 | 55 | 5.095007 | 2.638300 | 2.456708 |
| 34 | 1 | 1 | 0 | 0 | 0 | 1 | 7 | 9.832617 | 2.638300 | 7.194318 |
| 35 | 1 | 1 | 0 | 0 | 1 | 0 | 14 | -1.587808 | 2.638300 | -4.226108 |
| 36 | 1 | 1 | 0 | 0 | 1 | 1 | 4 | 8.761674 | 2.638300 | 6.123375 |
| 37 | 1 | 1 | 0 | 1 | 0 | 0 | 67 | 3.862593 | 2.638300 | 1.224293 |
| 38 | 1 | 1 | 0 | 1 | 0 | 1 | 17 | 3.162162 | 2.638300 | 0.523862 |
| 39 | 1 | 1 | 1 | 0 | 0 | 0 | 5 | 0.522196 | 2.638300 | -2.116104 |
| 40 | 1 | 1 | 1 | 0 | 0 | 1 | 2 | 7.826238 | 2.638300 | 5.187938 |
| 41 | 1 | 1 | 1 | 1 | 0 | 0 | 8 | 5.756044 | 2.638300 | 3.117744 |
| 42 | 1 | 1 | 1 | 1 | 0 | 1 | 4 | 5.440875 | 2.638300 | 2.802575 |
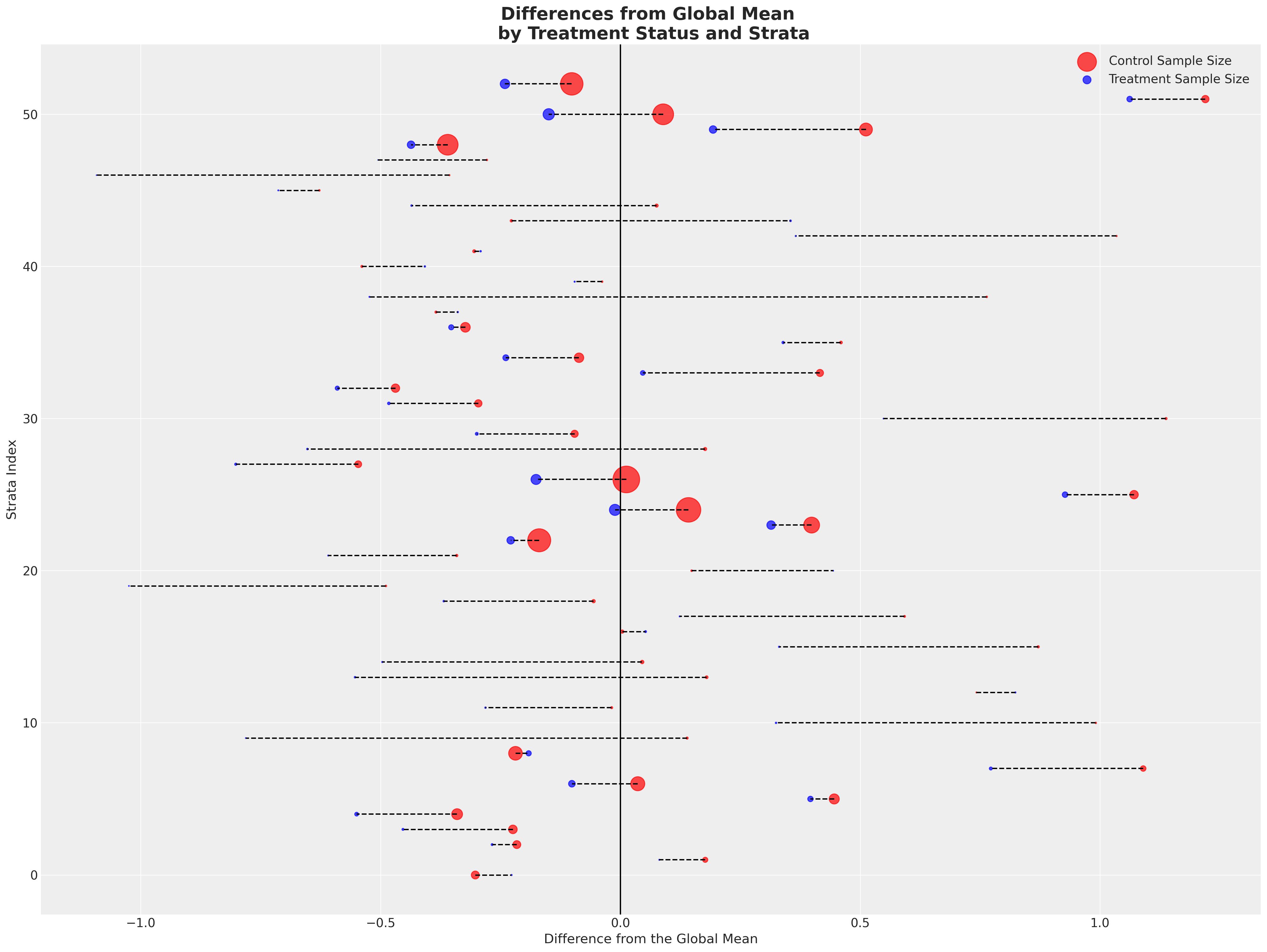
接下来我们将绘制两个组相对于全球平均值的偏差。这里每一行代表一个层,颜色表示该层属于哪个处理组。我们通过点的大小来区分层的大小。
Show code cell source
def make_strata_plot(strata_df):
joined_df = strata_df[strata_df["trt"] == 0].merge(
strata_df[strata_df["trt"] == 1], on=["sex", "race", "active_1", "active_2", "education_2"]
)
joined_df.sort_values("diff_y", inplace=True)
# Func to draw line segment
def newline(p1, p2, color="black"):
ax = plt.gca()
l = mlines.Line2D([p1[0], p2[0]], [p1[1], p2[1]], color="black", linestyle="--")
ax.add_line(l)
return l
fig, ax = plt.subplots(figsize=(20, 15))
ax.scatter(
joined_df["diff_x"],
joined_df.index,
color="red",
alpha=0.7,
label="Control Sample Size",
s=joined_df["outcome count_x"] * 3,
)
ax.scatter(
joined_df["diff_y"],
joined_df.index,
color="blue",
alpha=0.7,
label="Treatment Sample Size",
s=joined_df["outcome count_y"] * 3,
)
for i, p1, p2 in zip(joined_df.index, joined_df["diff_x"], joined_df["diff_y"]):
newline([p1, i], [p2, i])
ax.set_xlabel("Difference from the Global Mean")
ax.set_title(
"Differences from Global Mean \n by Treatment Status and Strata",
fontsize=20,
fontweight="bold",
)
ax.axvline(0, color="k")
ax.set_ylabel("Strata Index")
ax.legend()
make_strata_plot(strata_df)
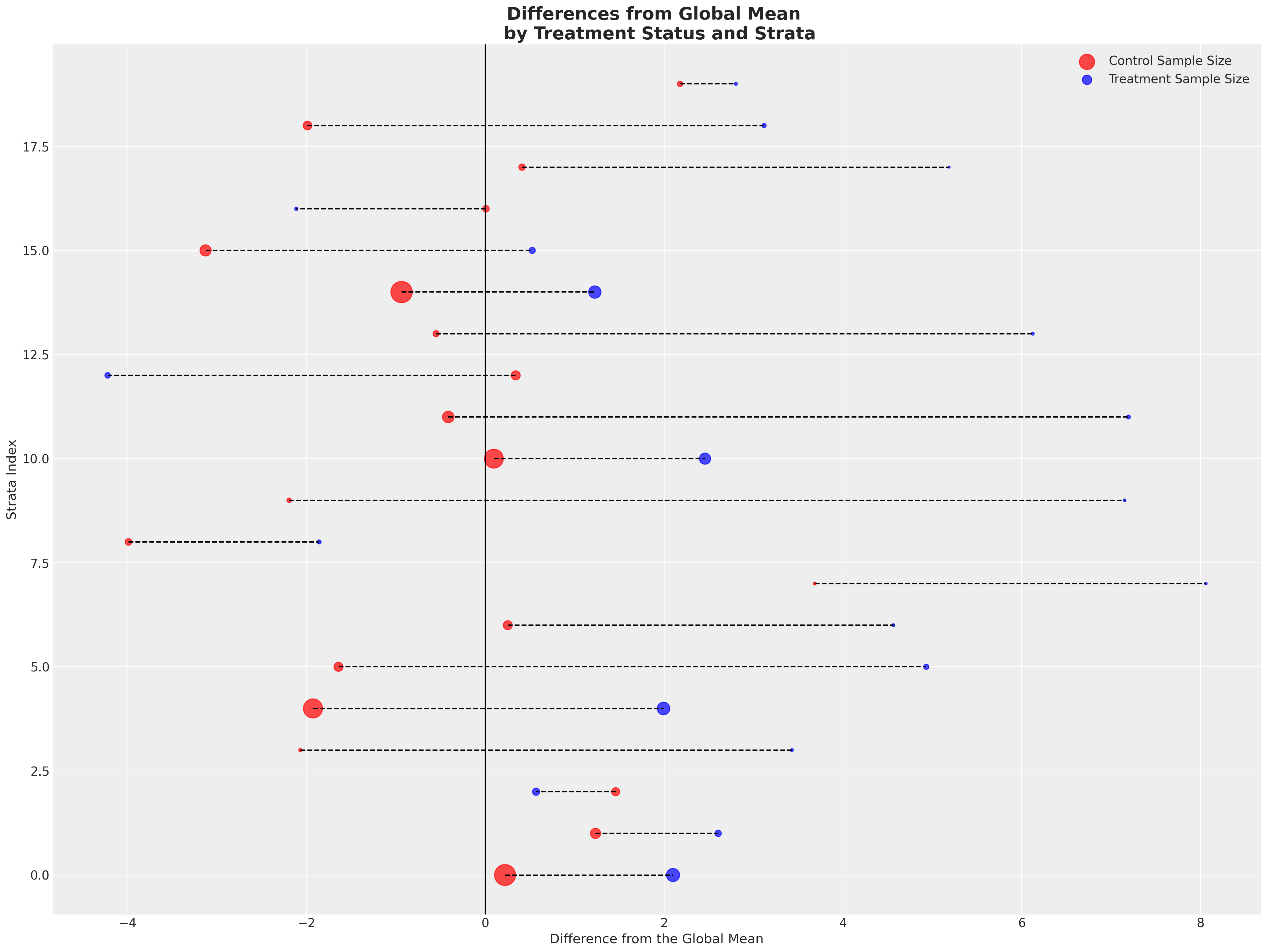
在各层中显示出相当一致的模式 - 治疗组在各层中几乎一致地实现了超过全球平均水平的成果。每个治疗组的样本量较小。然后,我们取各层特定平均值的平均值,以更清晰地区分差异。
strata_expected_df = strata_df.groupby("trt")[["outcome count", "outcome mean", "diff"]].agg(
{"outcome count": ["sum"], "outcome mean": "mean", "diff": "mean"}
)
print(
"Treatment Diff:",
strata_expected_df[("outcome mean", "mean")].iloc[1]
- strata_expected_df[("outcome mean", "mean")].iloc[0],
)
strata_expected_df
Treatment Diff: 3.662365976037309
| outcome count | outcome mean | diff | |
|---|---|---|---|
| sum | mean | mean | |
| trt | |||
| 0 | 1163 | 1.767384 | -0.870916 |
| 1 | 403 | 5.429750 | 2.791450 |
这种练习表明,我们的样本构建方式,即数据生成过程的某些方面,使得某些人口层级远离接受治疗组,而治疗组的存在则将结果变量向右拉动。接受治疗的倾向性是负相关的,因此会污染任何因果推断的声明。我们应当合理地担心,未能考虑到这种偏差可能会导致关于(a)戒断的方向和(b)戒断对体重影响的程度的错误结论。在观察性研究中,这是很自然的,我们从未有随机分配到治疗条件的情况,但通过建模治疗倾向性可以帮助我们模拟随机分配的条件。
准备建模数据#
我们现在只需以特定格式准备数据以供建模,从协变量数据 X 中移除 outcome 和 trt。
X = nhefs_df.copy()
y = nhefs_df["outcome"]
t = nhefs_df["trt"]
X = X.drop(["trt", "outcome"], axis=1)
X.head()
| age | race | sex | smokeintensity | smokeyrs | wt71 | active_1 | active_2 | education_2 | education_3 | education_4 | education_5 | exercise_1 | exercise_2 | age^2 | wt71^2 | smokeintensity^2 | smokeyrs^2 | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 0 | 42 | 1 | 0 | 30 | 29 | 79.04 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 1764 | 6247.3216 | 900 | 841 |
| 1 | 36 | 0 | 0 | 20 | 24 | 58.63 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 1296 | 3437.4769 | 400 | 576 |
| 2 | 56 | 1 | 1 | 20 | 26 | 56.81 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 1 | 3136 | 3227.3761 | 400 | 676 |
| 3 | 68 | 1 | 0 | 3 | 53 | 59.42 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 4624 | 3530.7364 | 9 | 2809 |
| 4 | 40 | 0 | 0 | 20 | 19 | 87.09 | 1 | 0 | 1 | 0 | 0 | 0 | 1 | 0 | 1600 | 7584.6681 | 400 | 361 |
倾向评分建模#
在这一步中,我们定义了一个模型构建函数,以捕捉治疗的概率,即每个个体的倾向评分。
我们指定了两种模型进行评估。一种是完全依赖逻辑回归的模型,另一种是使用BART(贝叶斯加性回归树)来建模协变量与治疗分配之间关系的模型。BART模型的优势在于使用基于树的算法来探索样本数据中各层之间的交互效应。有关BART和PyMC实现的更多详细信息,请参见这里。
拥有像BART这样的灵活模型是理解我们在进行逆倾向加权调整时所做工作的关键。我们的想法是,数据集中的任何给定层都将由一组协变量描述。个体的类型将由这些协变量配置文件表示——属性向量\(X\)。在我们的数据中,由任何给定协变量配置文件挑选出的观察结果的比例代表了对该类型个体的偏见。使用像BART这样的灵活模型对分配机制进行建模,使我们能够估计我们人口中一系列层的结局。
首先,我们将个体倾向评分建模为个体协变量剖面的函数:
def make_propensity_model(X, t, bart=True, probit=True, samples=1000, m=50):
coords = {"coeffs": list(X.columns), "obs": range(len(X))}
with pm.Model(coords=coords) as model_ps:
X_data = pm.MutableData("X", X)
t_data = pm.MutableData("t", t)
if bart:
mu = pmb.BART("mu", X, t, m=m)
if probit:
p = pm.Deterministic("p", pm.math.invprobit(mu))
else:
p = pm.Deterministic("p", pm.math.invlogit(mu))
else:
b = pm.Normal("b", mu=0, sigma=1, dims="coeffs")
mu = pm.math.dot(X_data, b)
p = pm.Deterministic("p", pm.math.invlogit(mu))
t_pred = pm.Bernoulli("t_pred", p=p, observed=t_data, dims="obs")
idata = pm.sample_prior_predictive()
idata.extend(pm.sample(samples, random_seed=105, idata_kwargs={"log_likelihood": True}))
idata.extend(pm.sample_posterior_predictive(idata))
return model_ps, idata
m_ps_logit, idata_logit = make_propensity_model(X, t, bart=False, samples=1000)
Sampling: [b, t_pred]
Auto-assigning NUTS sampler...
Initializing NUTS using jitter+adapt_diag...
Multiprocess sampling (4 chains in 4 jobs)
NUTS: [b]
Sampling 4 chains for 1_000 tune and 1_000 draw iterations (4_000 + 4_000 draws total) took 138 seconds.
Sampling: [t_pred]
m_ps_probit, idata_probit = make_propensity_model(X, t, bart=True, probit=True, samples=4000)
Sampling: [mu, t_pred]
Multiprocess sampling (4 chains in 4 jobs)
PGBART: [mu]
Sampling 4 chains for 1_000 tune and 4_000 draw iterations (4_000 + 16_000 draws total) took 109 seconds.
The rhat statistic is larger than 1.01 for some parameters. This indicates problems during sampling. See https://arxiv.org/abs/1903.08008 for details
The effective sample size per chain is smaller than 100 for some parameters. A higher number is needed for reliable rhat and ess computation. See https://arxiv.org/abs/1903.08008 for details
Sampling: [t_pred]
使用倾向评分:权重和伪群体#
一旦我们拟合了这些模型,我们就可以比较每个模型如何将治疗的倾向性(在我们的例子中是戒烟的倾向性)归因于每个被测量的个体。让我们绘制研究中前20个左右个体的倾向评分分布图,以查看两个模型之间的差异。
az.plot_forest(
[idata_logit, idata_probit],
var_names=["p"],
coords={"p_dim_0": range(20)},
figsize=(10, 13),
combined=True,
kind="ridgeplot",
model_names=["Logistic Regression", "BART"],
r_hat=True,
ridgeplot_alpha=0.4,
);
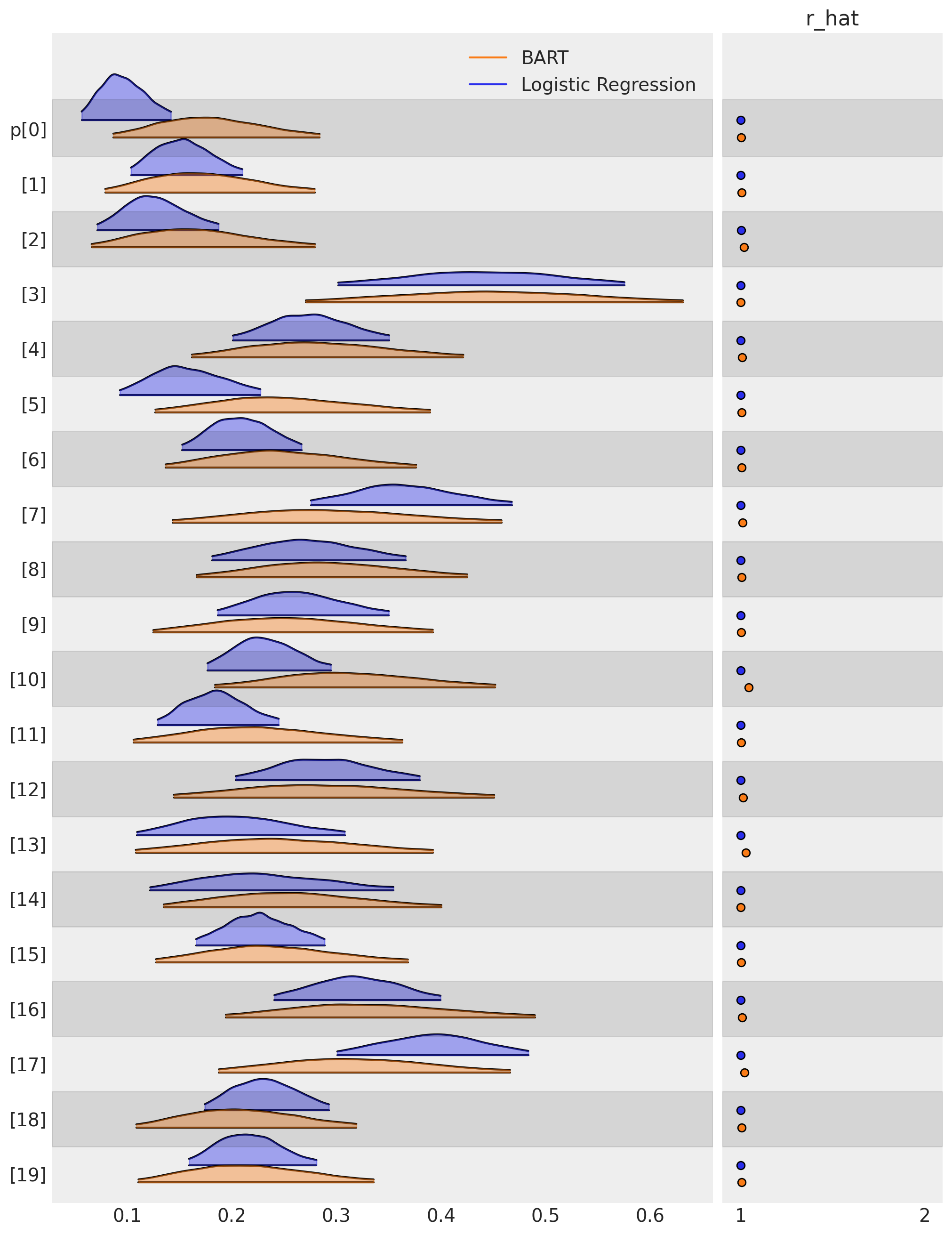
这些倾向评分可以被提取出来,并与其他协变量一起进行检查。
ps_logit = idata_logit["posterior"]["p"].mean(dim=("chain", "draw")).round(2)
ps_logit
<xarray.DataArray 'p' (p_dim_0: 1566)> array([0.1 , 0.15, 0.13, ..., 0.13, 0.47, 0.18]) Coordinates: * p_dim_0 (p_dim_0) int64 0 1 2 3 4 5 6 ... 1560 1561 1562 1563 1564 1565
ps_probit = idata_probit["posterior"]["p"].mean(dim=("chain", "draw")).round(2)
ps_probit
<xarray.DataArray 'p' (p_dim_0: 1566)> array([0.18, 0.18, 0.17, ..., 0.16, 0.32, 0.28]) Coordinates: * p_dim_0 (p_dim_0) int64 0 1 2 3 4 5 6 ... 1560 1561 1562 1563 1564 1565
在这里,我们绘制了每个模型下倾向评分分布,并展示了如何将倾向评分的倒数权重应用于观测数据点。
Show code cell source
fig, axs = plt.subplots(3, 2, figsize=(20, 15))
axs = axs.flatten()
colors = {1: "blue", 0: "red"}
axs[0].hist(ps_logit.values[t == 0], ec="black", color="red", bins=30, label="Control", alpha=0.6)
axs[0].hist(
ps_logit.values[t == 1], ec="black", color="blue", bins=30, label="Treatment", alpha=0.6
)
axs[2].hist(ps_logit.values[t == 0], ec="black", color="red", bins=30, label="Control", alpha=0.6)
axs[2].hist(
1 - ps_logit.values[t == 1], ec="black", color="blue", bins=30, label="Treatment", alpha=0.6
)
axs[0].set_xlabel("Propensity Scores")
axs[1].set_xlabel("Propensity Scores")
axs[1].set_ylabel("Count of Observations")
axs[0].set_ylabel("Count of Observations")
axs[0].axvline(0.9, color="black", linestyle="--", label="Extreme Propensity Score")
axs[0].axvline(0.1, color="black", linestyle="--")
axs[1].hist(ps_probit.values[t == 0], ec="black", color="red", bins=30, label="Control", alpha=0.6)
axs[1].hist(
ps_probit.values[t == 1], ec="black", color="blue", bins=30, label="Treatment", alpha=0.6
)
axs[3].hist(ps_probit.values[t == 0], ec="black", color="red", bins=30, label="Control", alpha=0.6)
axs[3].hist(
1 - ps_probit.values[t == 1], ec="black", color="blue", bins=30, label="Treatment", alpha=0.6
)
axs[3].set_title("Overlap of inverted Propensity Scores")
axs[2].set_title("Overlap of inverted Propensity Scores")
axs[1].axvline(0.9, color="black", linestyle="--", label="Extreme Propensity Score")
axs[1].axvline(0.1, color="black", linestyle="--")
axs[2].axvline(0.9, color="black", linestyle="--", label="Extreme Propensity Score")
axs[2].axvline(0.1, color="black", linestyle="--")
axs[3].axvline(0.9, color="black", linestyle="--", label="Extreme Propensity Score")
axs[3].axvline(0.1, color="black", linestyle="--")
axs[0].set_xlim(0, 1)
axs[1].set_xlim(0, 1)
axs[0].set_title("Propensity Scores under Logistic Regression", fontsize=20)
axs[1].set_title(
"Propensity Scores under Non-Parametric BART model \n with probit transform", fontsize=20
)
axs[4].scatter(
X["age"], y, color=t.map(colors), s=(1 / ps_logit.values) * 20, ec="black", alpha=0.4
)
axs[4].set_xlabel("Age")
axs[5].set_xlabel("Age")
axs[5].set_ylabel("y")
axs[4].set_ylabel("y")
axs[4].set_title("Sized by IP Weights")
axs[5].set_title("Sized by IP Weights")
axs[5].scatter(
X["age"], y, color=t.map(colors), s=(1 / ps_probit.values) * 20, ec="black", alpha=0.4
)
red_patch = mpatches.Patch(color="red", label="Control")
blue_patch = mpatches.Patch(color="blue", label="Treated")
axs[2].legend(handles=[red_patch, blue_patch])
axs[0].legend()
axs[1].legend()
axs[5].legend(handles=[red_patch, blue_patch]);
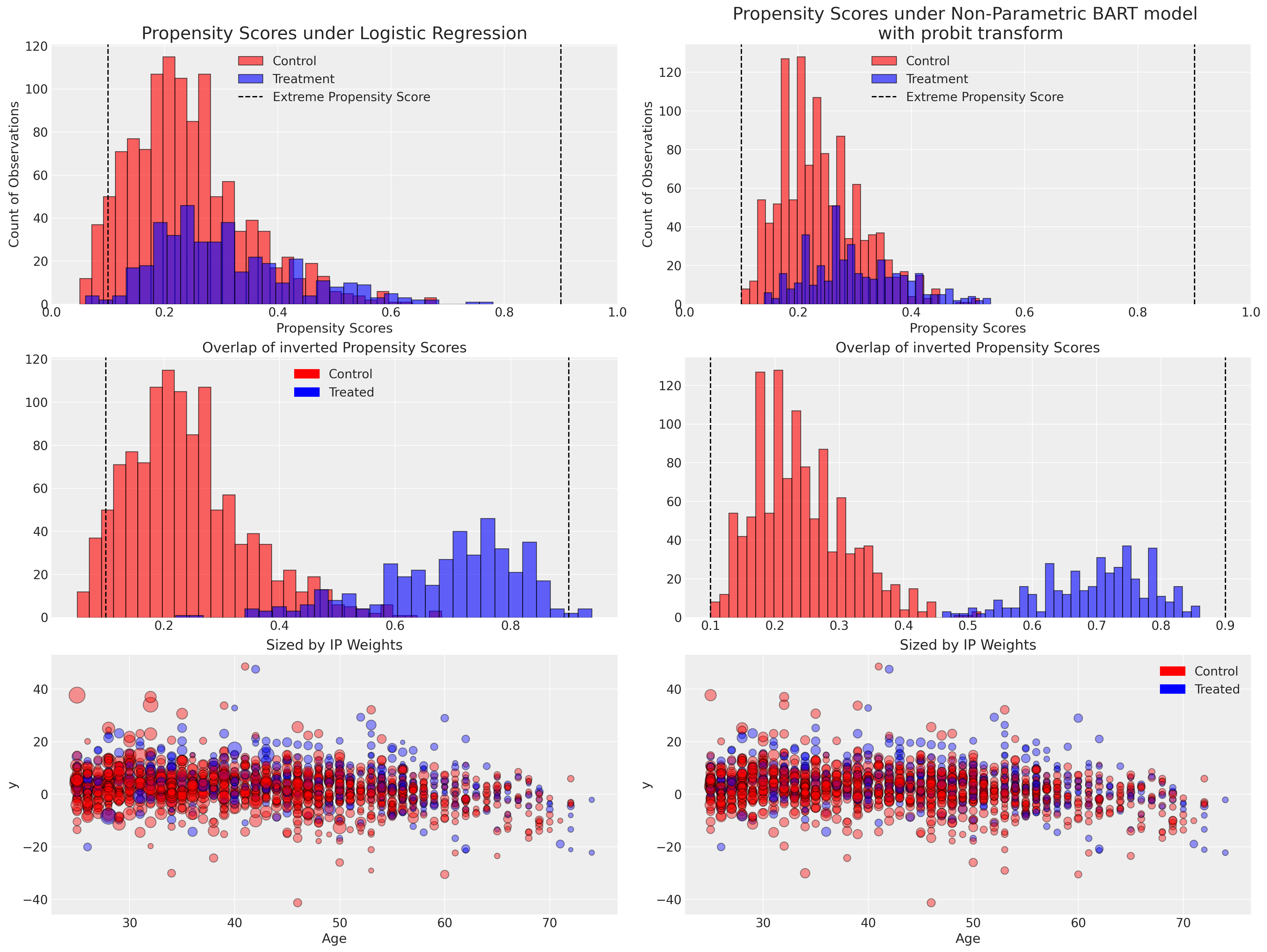
当我们考虑倾向评分分布时,我们寻找的是正性,即在任何由协变量值组合定义的患者亚组中,接受给定治疗的条件概率不能为0或1。我们不希望过度拟合我们的倾向模型,并实现完美的治疗/对照组分配,因为这会降低它们在加权方案中的有用性。倾向评分的重要特征是它们是衡量组间相似性的指标——极端预测值为0或1会威胁因果治疗效果的可识别性。在某些协变量剖面定义的层内,极端倾向评分表明模型不认为这些个体之间的治疗对比可以很好地定义。或者至少,对比组之一的样本量会非常小。一些作者建议在(.1, .9)处划定界限,以过滤或限制极端情况,以解决这种过度拟合问题,但这本质上是对模型错误指定的承认。
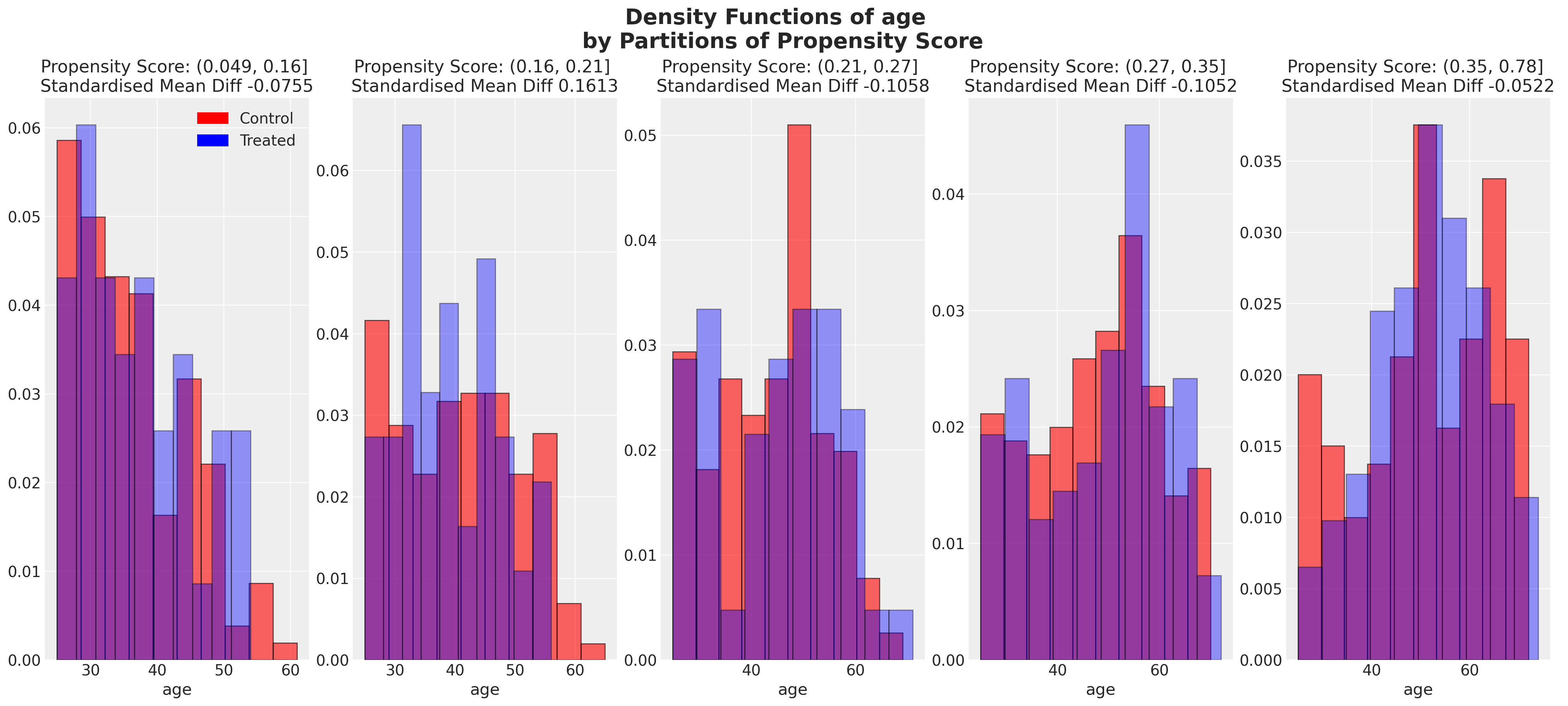
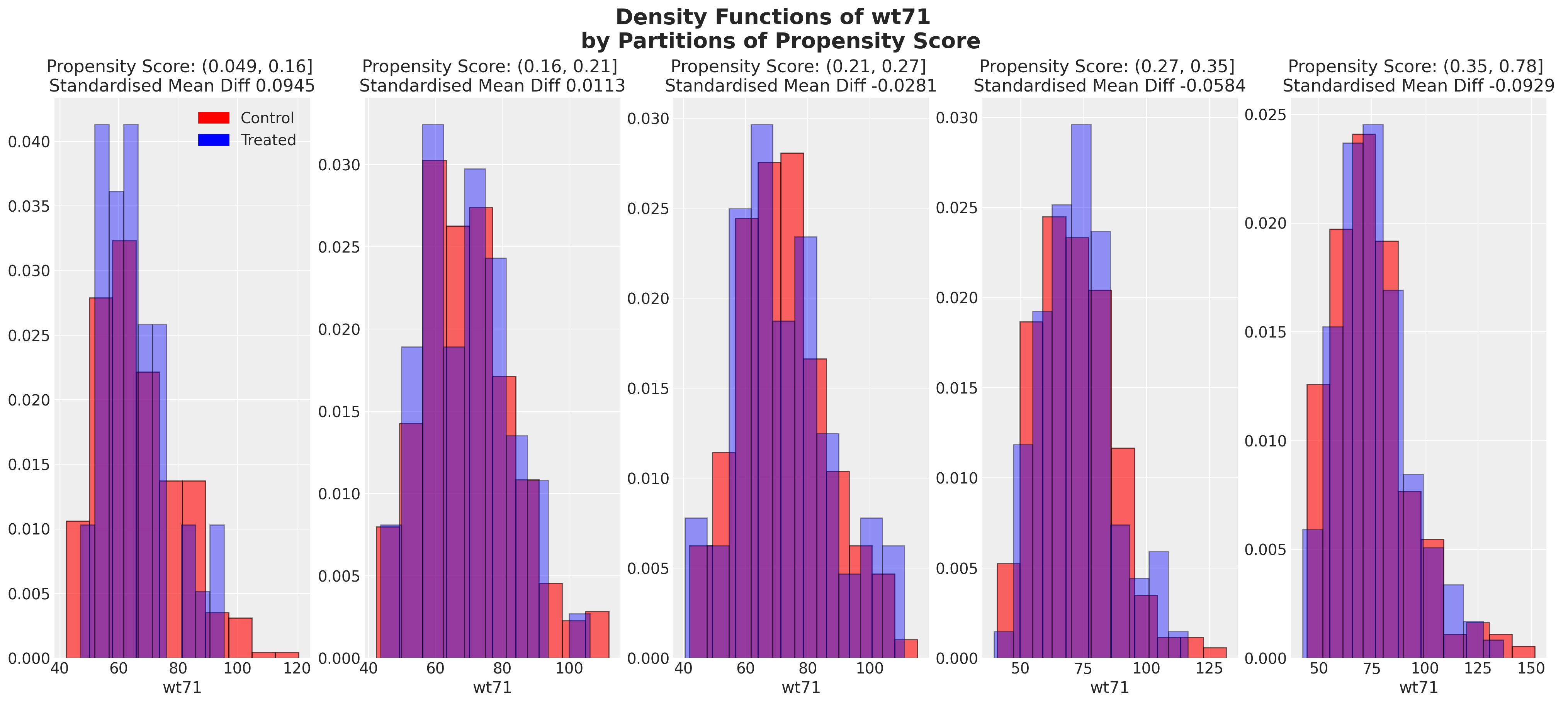
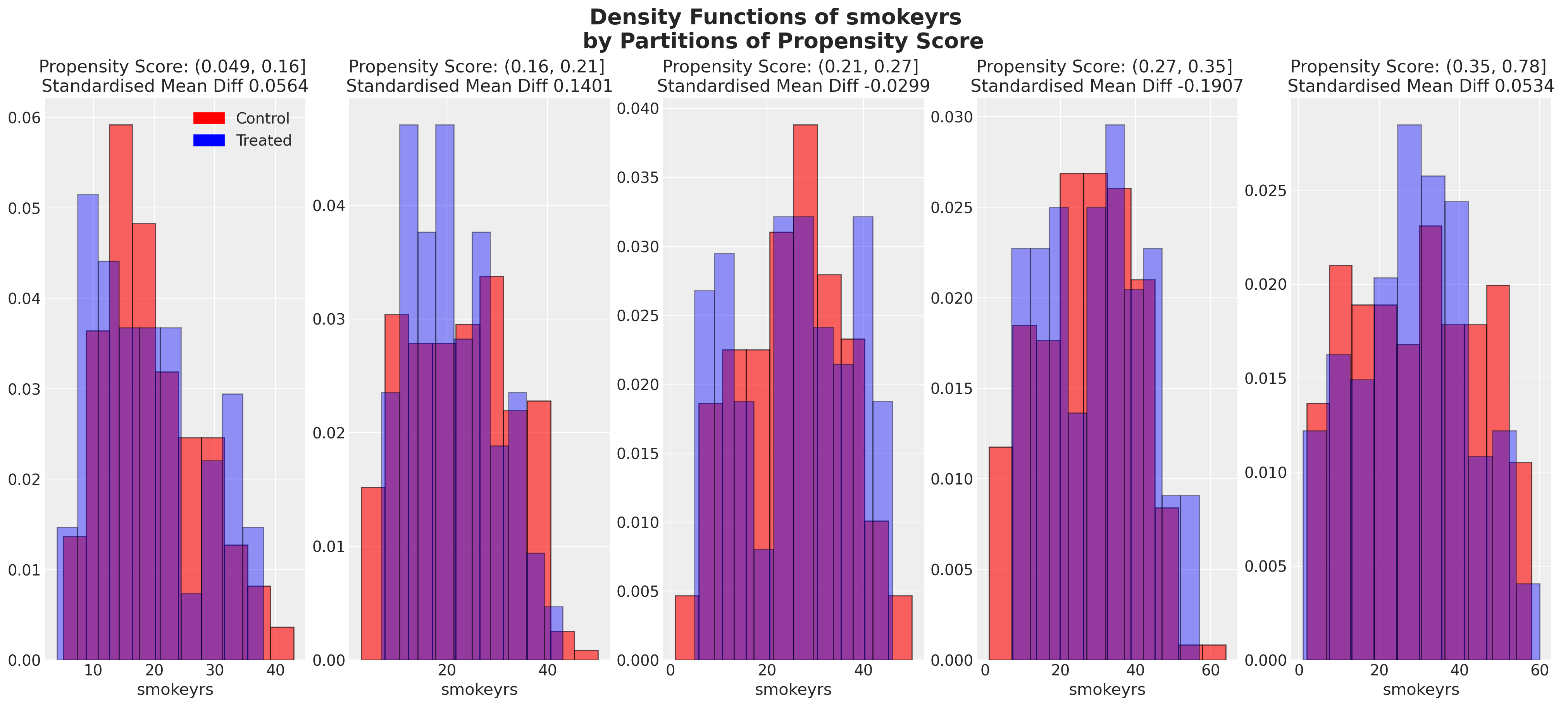
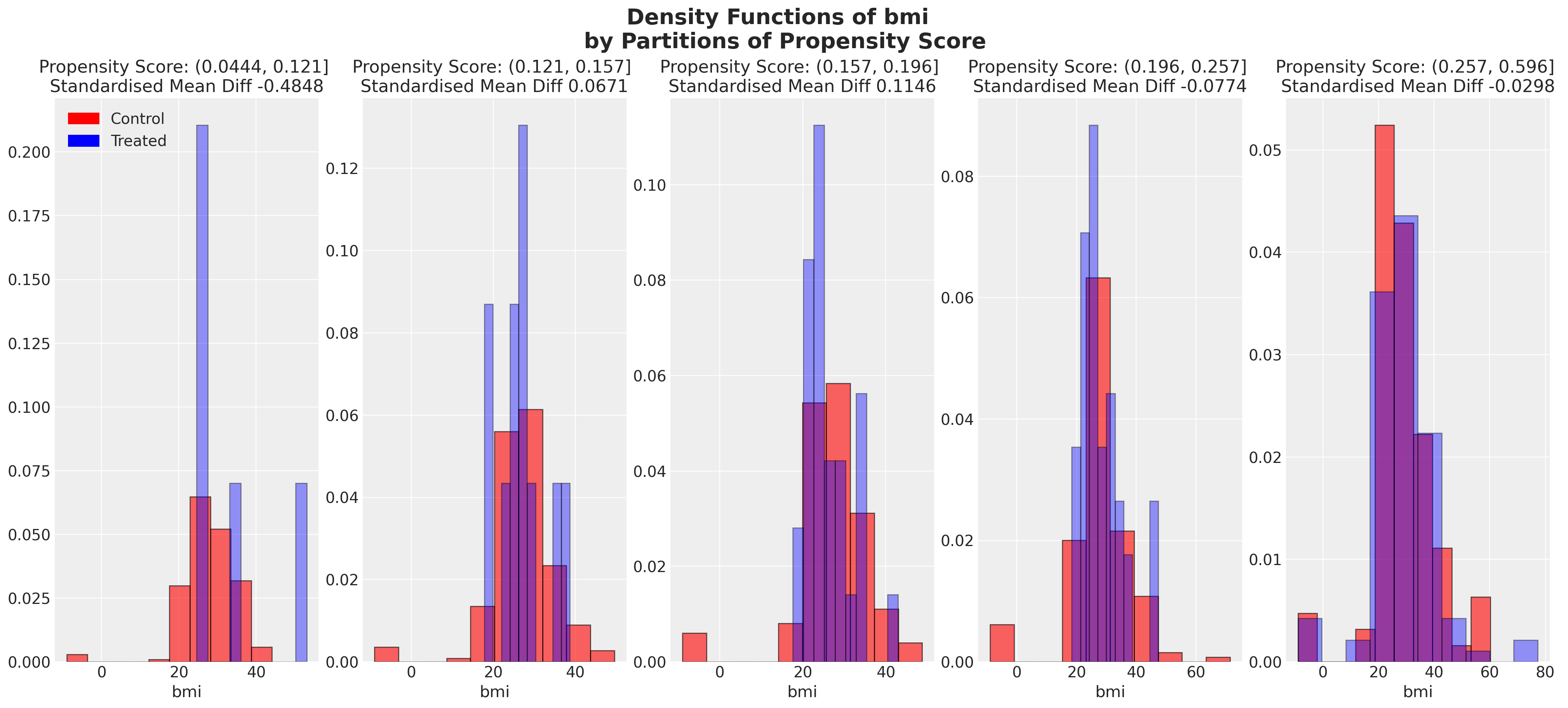
我们还可以查看倾向评分各分区中协变量的平衡情况。这类图表帮助我们评估在倾向评分条件下,我们的样本在处理组和对照组之间是否呈现出平衡的特征。我们旨在展示在倾向评分条件下的协变量特征的平衡。
Show code cell source
temp = X.copy()
temp["ps"] = ps_logit.values
temp["ps_cut"] = pd.qcut(temp["ps"], 5)
def plot_balance(temp, col, t):
fig, axs = plt.subplots(1, 5, figsize=(20, 9))
axs = axs.flatten()
for c, ax in zip(np.sort(temp["ps_cut"].unique()), axs):
std0 = temp[(t == 0) & (temp["ps_cut"] == c)][col].std()
std1 = temp[(t == 1) & (temp["ps_cut"] == c)][col].std()
pooled_std = (std0 + std1) / 2
mean_diff = (
temp[(t == 0) & (temp["ps_cut"] == c)][col].mean()
- temp[(t == 1) & (temp["ps_cut"] == c)][col].mean()
) / pooled_std
ax.hist(
temp[(t == 0) & (temp["ps_cut"] == c)][col],
alpha=0.6,
color="red",
density=True,
ec="black",
bins=10,
cumulative=False,
)
ax.hist(
temp[(t == 1) & (temp["ps_cut"] == c)][col],
alpha=0.4,
color="blue",
density=True,
ec="black",
bins=10,
cumulative=False,
)
ax.set_title(f"Propensity Score: {c} \n Standardised Mean Diff {np.round(mean_diff, 4)} ")
ax.set_xlabel(col)
red_patch = mpatches.Patch(color="red", label="Control")
blue_patch = mpatches.Patch(color="blue", label="Treated")
axs[0].legend(handles=[red_patch, blue_patch])
plt.suptitle(
f"Density Functions of {col} \n by Partitions of Propensity Score",
fontsize=20,
fontweight="bold",
)
plot_balance(temp, "age", t)
plot_balance(temp, "wt71", t)
plot_balance(temp, "smokeyrs", t)
plot_balance(temp, "smokeintensity", t)
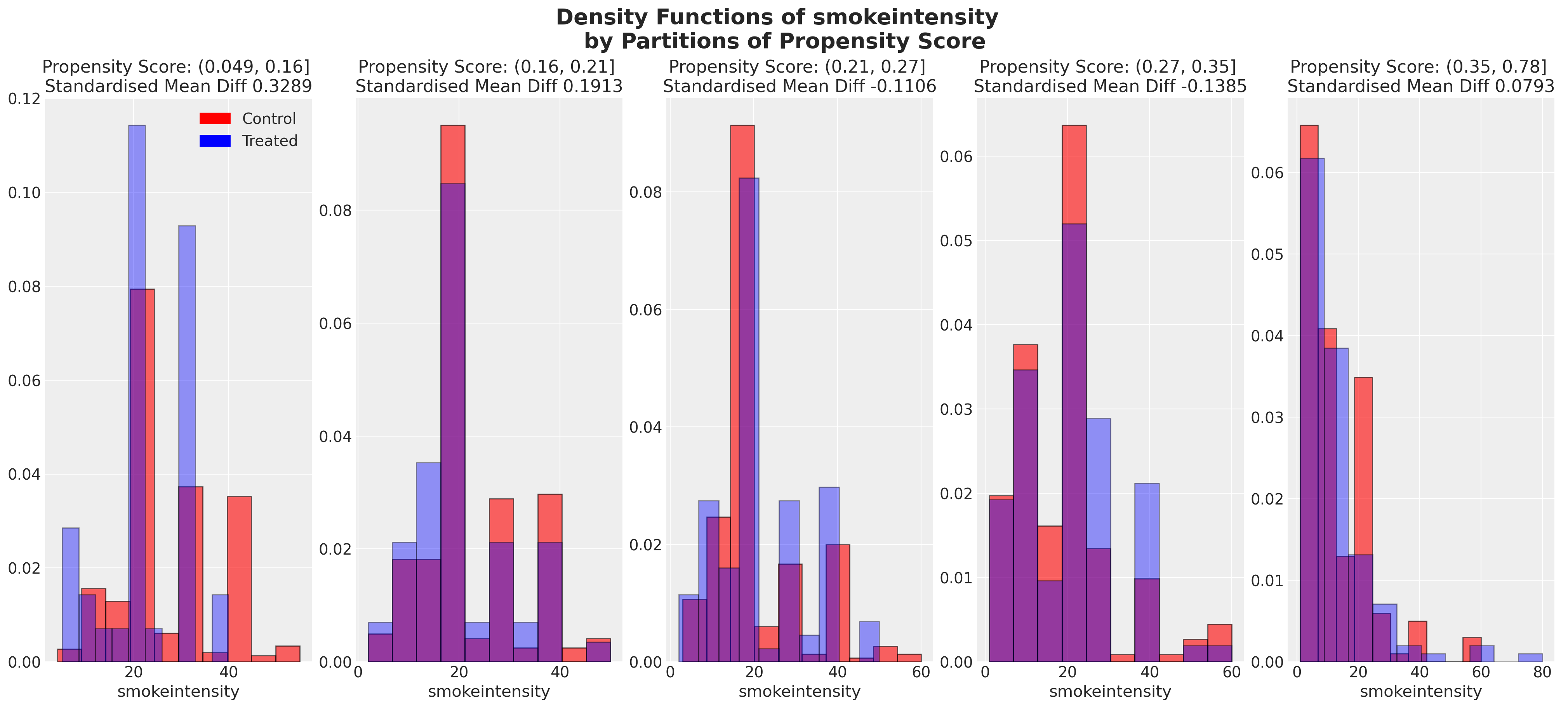
在一个理想的世界中,我们会在每个协变量上对治疗组实现完美的平衡,但即使像我们在这里看到的近似平衡也是有用的。当我们有良好的协变量平衡(在倾向评分条件下)时,我们可以将倾向评分用于加权方案中的统计摘要模型,以便在两个组之间“纠正”协变量剖面的表示。如果个体的倾向评分使得他们极有可能接受治疗状态,例如0.95,那么如果他们在治疗组中出现,我们希望降低他们的重要性,如果他们在对照组中出现,我们希望增加他们的重要性。这是有道理的,因为他们的倾向评分高意味着类似个体已经在治疗组中大量存在,但在对照组中出现的可能性较小。因此,我们的纠正策略是重新调整他们在每个组中对摘要统计的贡献。
稳健和双重稳健加权方案#
我们一直强调倾向得分权重是一种修正方法。这是因果分析者调整处理组和对照组中个体代表性份额的机会。然而,没有普遍适用的修正方法,因此自然出现了各种替代方案来填补简单倾向得分加权失败的空白。我们将在下面看到一些替代的加权方案。
需要特别指出的是原始倾向评分权重与双重稳健倾向评分权重理论之间的区别。
双重稳健方法之所以如此命名,是因为它们代表了因果效应的折衷估计量,结合了(i)处理分配模型(如倾向评分)和(ii)更直接的响应结果模型。该方法以一种生成统计上无偏的处理效应估计的方式结合了这两个估计量。它们效果良好,因为它们的结合方式要求只需要其中一个模型被正确指定。分析人员选择其加权方案的组成部分,只要他们相信自己正确地建模了(i)或(ii)中的任何一个。这在“基于设计的”推断和“基于模型的”推断之间的明显区别中形成了一种有趣的紧张关系——双重稳健估计器的要求在某种程度上是对纯粹方法论者的让步;我们需要两者,并且不明显何时单独使用其中一个就足够了。
估计治疗效果#
在本节中,我们构建了一组函数,用于从我们的倾向得分后验分布中提取并提取一个样本;使用此倾向得分对我们的处理组和对照组之间的观察结果变量进行重新加权,以重新计算平均处理效应(ATE)。它使用三种逆概率加权方案之一对我们的数据进行重新加权,然后绘制三个视图(1)各组之间的原始倾向得分(2)原始结果分布(3)重新加权的结果分布。
首先,我们为将要探索的每种权重调整方法定义了一堆辅助函数:
def make_robust_adjustments(X, t):
X["trt"] = t
p_of_t = X["trt"].mean()
X["i_ps"] = np.where(t, (p_of_t / X["ps"]), (1 - p_of_t) / (1 - X["ps"]))
n_ntrt = X[X["trt"] == 0].shape[0]
n_trt = X[X["trt"] == 1].shape[0]
outcome_trt = X[X["trt"] == 1]["outcome"]
outcome_ntrt = X[X["trt"] == 0]["outcome"]
i_propensity0 = X[X["trt"] == 0]["i_ps"]
i_propensity1 = X[X["trt"] == 1]["i_ps"]
weighted_outcome1 = outcome_trt * i_propensity1
weighted_outcome0 = outcome_ntrt * i_propensity0
return weighted_outcome0, weighted_outcome1, n_ntrt, n_trt
def make_raw_adjustments(X, t):
X["trt"] = t
X["ps"] = np.where(X["trt"], X["ps"], 1 - X["ps"])
X["i_ps"] = 1 / X["ps"]
n_ntrt = n_trt = len(X)
outcome_trt = X[X["trt"] == 1]["outcome"]
outcome_ntrt = X[X["trt"] == 0]["outcome"]
i_propensity0 = X[X["trt"] == 0]["i_ps"]
i_propensity1 = X[X["trt"] == 1]["i_ps"]
weighted_outcome1 = outcome_trt * i_propensity1
weighted_outcome0 = outcome_ntrt * i_propensity0
return weighted_outcome0, weighted_outcome1, n_ntrt, n_trt
def make_doubly_robust_adjustment(X, t, y):
m0 = sm.OLS(y[t == 0], X[t == 0].astype(float)).fit()
m1 = sm.OLS(y[t == 1], X[t == 1].astype(float)).fit()
m0_pred = m0.predict(X)
m1_pred = m1.predict(X)
X["trt"] = t
X["y"] = y
## Compromise between outcome and treatement assignment model
weighted_outcome0 = (1 - X["trt"]) * (X["y"] - m0_pred) / (1 - X["ps"]) + m0_pred
weighted_outcome1 = X["trt"] * (X["y"] - m1_pred) / X["ps"] + m1_pred
return weighted_outcome0, weighted_outcome1, None, None
这里值得扩展一下双重稳健估计的理论。我们在上面展示了实现处理分配估计量和响应或结果估计量之间折衷的代码。但为什么这很有用呢?考虑双重稳健估计量的函数形式。
这些公式如何影响结果模型和处理分配模型之间的妥协并不是立即直观的。但考虑极端情况。首先想象我们的模型 \(m_{1}\) 是结果 \(Y\) 的完美拟合,那么分数的分子为0,我们最终得到模型预测的平均值。相反,想象模型 \(m_{1}\) 被错误指定,并且我们在分子中有一些误差 \(\epsilon > 0\)。如果倾向评分模型是准确的,那么在处理类中我们的分母应该很高……比如说 \(\sim N(.9, .05)\),因此估计器将接近 \(\epsilon\) 的数加回到 \(m_{1}\) 预测中。类似的推理也适用于 \(Y(0)\) 的情况。
其他估计器则更为简单——通过估计倾向得分的一系列变换来对结果变量进行缩放。每个估计器都是试图通过我们所了解的治疗倾向来重新平衡数据点。但这些估计器之间的差异(正如我们将看到的)在它们的应用中是重要的。
现在我们定义原始和重新加权结果的绘图函数。
Show code cell source
def plot_weights(bins, top0, top1, ylim, ax):
ax.axhline(0, c="gray", linewidth=1)
ax.set_ylim(ylim)
bars0 = ax.bar(bins[:-1] + 0.025, top0, width=0.04, facecolor="red", alpha=0.6)
bars1 = ax.bar(bins[:-1] + 0.025, -top1, width=0.04, facecolor="blue", alpha=0.6)
for bars in (bars0, bars1):
for bar in bars:
bar.set_edgecolor("black")
for x, y in zip(bins, top0):
ax.text(x + 0.025, y + 10, str(y), ha="center", va="bottom")
for x, y in zip(bins, top1):
ax.text(x + 0.025, -y - 10, str(y), ha="center", va="top")
def make_plot(
X,
idata,
lower_bins=[np.arange(1, 30, 1), np.arange(1, 30, 1)],
ylims=[
(-100, 370),
(
-40,
100,
),
(-50, 110),
],
text_pos=(20, 80),
ps=None,
method="robust",
):
X = X.copy()
if ps is None:
n_list = list(range(1000))
## Choose random ps score from posterior
choice = np.random.choice(n_list, 1)[0]
X["ps"] = idata["posterior"]["p"].stack(z=("chain", "draw"))[:, choice].values
else:
X["ps"] = ps
X["trt"] = t
propensity0 = X[X["trt"] == 0]["ps"]
propensity1 = X[X["trt"] == 1]["ps"]
## Get Weighted Outcomes
if method == "robust":
X["outcome"] = y
weighted_outcome0, weighted_outcome1, n_ntrt, n_trt = make_robust_adjustments(X, t)
elif method == "raw":
X["outcome"] = y
weighted_outcome0, weighted_outcome1, n_ntrt, n_trt = make_raw_adjustments(X, t)
else:
weighted_outcome0, weighted_outcome1, _, _ = make_doubly_robust_adjustment(X, t, y)
### Top Plot of Propensity Scores
bins = np.arange(0.025, 0.85, 0.05)
top0, _ = np.histogram(propensity0, bins=bins)
top1, _ = np.histogram(propensity1, bins=bins)
fig, axs = plt.subplots(3, 1, figsize=(20, 20))
axs = axs.flatten()
plot_weights(bins, top0, top1, ylims[0], axs[0])
axs[0].text(0.05, 230, "Control = 0")
axs[0].text(0.05, -90, "Treatment = 1")
axs[0].set_ylabel("No. Patients", fontsize=14)
axs[0].set_xlabel("Estimated Propensity Score", fontsize=14)
axs[0].set_title(
"Inferred Propensity Scores and IP Weighted Outcome \n by Treatment and Control",
fontsize=20,
)
### Middle Plot of Outcome
outcome_trt = y[t == 1]
outcome_ntrt = y[t == 0]
top0, _ = np.histogram(outcome_ntrt, bins=lower_bins[0])
top1, _ = np.histogram(outcome_trt, bins=lower_bins[0])
plot_weights(lower_bins[0], top0, top1, ylims[2], axs[1])
axs[1].set_ylabel("No. Patients", fontsize=14)
axs[1].set_xlabel("Raw Outcome Measure", fontsize=14)
axs[1].text(text_pos[0], text_pos[1], f"Control: E(Y) = {outcome_ntrt.mean()}")
axs[1].text(text_pos[0], text_pos[1] - 20, f"Treatment: E(Y) = {outcome_trt.mean()}")
axs[1].text(
text_pos[0],
text_pos[1] - 40,
f"tau: E(Y(1) - Y(0)) = {outcome_trt.mean()- outcome_ntrt.mean()}",
fontweight="bold",
)
## Bottom Plot of Adjusted Outcome using Inverse Propensity Score weights
axs[2].set_ylabel("No. Patients", fontsize=14)
if method in ["raw", "robust"]:
top0, _ = np.histogram(weighted_outcome0, bins=lower_bins[1])
top1, _ = np.histogram(weighted_outcome1, bins=lower_bins[1])
plot_weights(lower_bins[1], top0, top1, ylims[1], axs[2])
axs[2].set_xlabel("Estimated IP Weighted Outcome \n Shifted", fontsize=14)
axs[2].text(text_pos[0], text_pos[1], f"Control: E(Y) = {weighted_outcome0.sum() / n_ntrt}")
axs[2].text(
text_pos[0], text_pos[1] - 20, f"Treatment: E(Y) = {weighted_outcome1.sum() / n_trt}"
)
axs[2].text(
text_pos[0],
text_pos[1] - 40,
f"tau: E(Y(1) - Y(0)) = {weighted_outcome1.sum() / n_trt - weighted_outcome0.sum() / n_ntrt}",
fontweight="bold",
)
else:
top0, _ = np.histogram(weighted_outcome0, bins=lower_bins[1])
top1, _ = np.histogram(weighted_outcome1, bins=lower_bins[1])
plot_weights(lower_bins[1], top0, top1, ylims[1], axs[2])
trt = np.round(np.mean(weighted_outcome1), 5)
ntrt = np.round(np.mean(weighted_outcome0), 5)
axs[2].set_xlabel("Estimated IP Weighted Outcome \n Shifted", fontsize=14)
axs[2].text(text_pos[0], text_pos[1], f"Control: E(Y) = {ntrt}")
axs[2].text(text_pos[0], text_pos[1] - 20, f"Treatment: E(Y) = {trt}")
axs[2].text(
text_pos[0], text_pos[1] - 40, f"tau: E(Y(1) - Y(0)) = {trt - ntrt}", fontweight="bold"
)
Logit倾向模型#
我们使用稳健的倾向评分估计方法绘制结果和重新加权的结果分布。
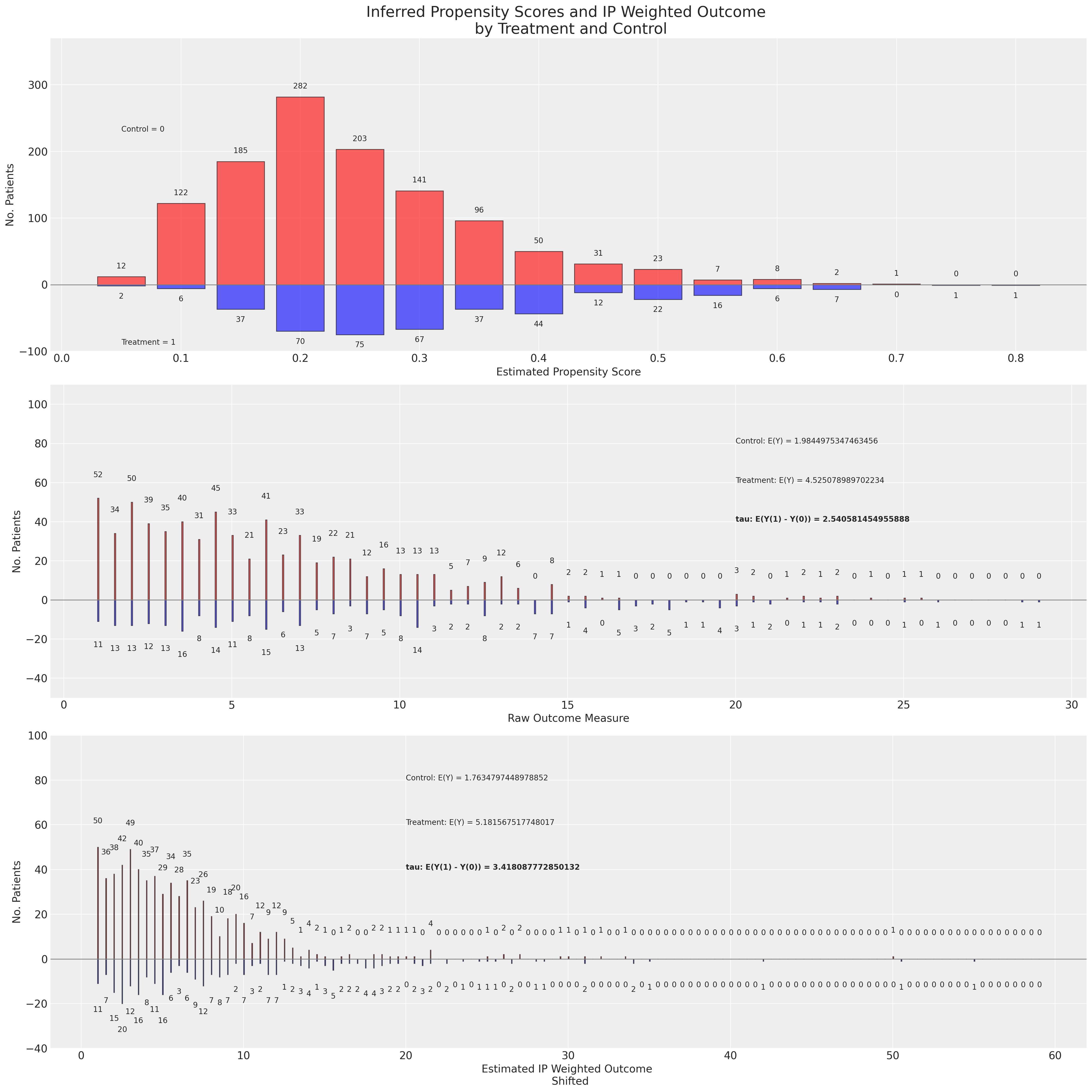
这个图中有许多内容,因此值得稍微放慢速度来逐步解释。在第一个面板中,我们展示了处理组和对照组之间的倾向评分分布。在第二个面板中,我们将原始结果数据再次绘制为按组划分的分布。此外,我们还展示了在原始结果数据上天真估计的预期结果值和ATE。最后,在第三个面板中,我们展示了使用逆倾向评分重新加权后的结果变量,并基于调整后的结果变量推导出ATE。我们在这个图中强调的是原始结果和调整后结果下的ATE之间的区别。
接下来,由于我们是贝叶斯主义者——我们提取并评估基于采样倾向得分得出的ATE的后验分布。我们在上面看到了ATE的点估计,但在因果推断的背景下,理解估计中的不确定性往往更为重要。
def get_ate(X, t, y, i, idata, method="doubly_robust"):
X = X.copy()
X["outcome"] = y
### Post processing the sample posterior distribution for propensity scores
### One sample at a time.
X["ps"] = idata["posterior"]["p"].stack(z=("chain", "draw"))[:, i].values
if method == "robust":
weighted_outcome_ntrt, weighted_outcome_trt, n_ntrt, n_trt = make_robust_adjustments(X, t)
ntrt = weighted_outcome_ntrt.sum() / n_ntrt
trt = weighted_outcome_trt.sum() / n_trt
elif method == "raw":
weighted_outcome_ntrt, weighted_outcome_trt, n_ntrt, n_trt = make_raw_adjustments(X, t)
ntrt = weighted_outcome_ntrt.sum() / n_ntrt
trt = weighted_outcome_trt.sum() / n_trt
else:
X.drop("outcome", axis=1, inplace=True)
weighted_outcome_ntrt, weighted_outcome_trt, n_ntrt, n_trt = make_doubly_robust_adjustment(
X, t, y
)
trt = np.mean(weighted_outcome_trt)
ntrt = np.mean(weighted_outcome_ntrt)
ate = trt - ntrt
return [ate, trt, ntrt]
qs = range(4000)
ate_dist = [get_ate(X, t, y, q, idata_logit, method="robust") for q in qs]
ate_dist_df_logit = pd.DataFrame(ate_dist, columns=["ATE", "E(Y(1))", "E(Y(0))"])
ate_dist_df_logit.head()
| ATE | E(Y(1)) | E(Y(0)) | |
|---|---|---|---|
| 0 | 3.649712 | 5.460591 | 1.810880 |
| 1 | 3.226628 | 4.998798 | 1.772170 |
| 2 | 3.700728 | 5.406525 | 1.705797 |
| 3 | 3.350942 | 5.167095 | 1.816153 |
| 4 | 4.156807 | 5.784731 | 1.627924 |
接下来我们绘制ATE的后验分布。
Show code cell source
def plot_ate(ate_dist_df, xy=(4.0, 250)):
fig, axs = plt.subplots(1, 2, figsize=(20, 7))
axs = axs.flatten()
axs[0].hist(
ate_dist_df["E(Y(1))"], bins=30, ec="black", color="blue", label="E(Y(1))", alpha=0.5
)
axs[0].hist(
ate_dist_df["E(Y(0))"], bins=30, ec="black", color="red", label="E(Y(0))", alpha=0.7
)
axs[1].hist(ate_dist_df["ATE"], bins=30, ec="black", color="slateblue", label="ATE", alpha=0.6)
ate = np.round(ate_dist_df["ATE"].mean(), 2)
axs[1].axvline(ate, label="E(ATE)", linestyle="--", color="black")
axs[1].annotate(f"E(ATE): {ate}", xy, fontsize=20, fontweight="bold")
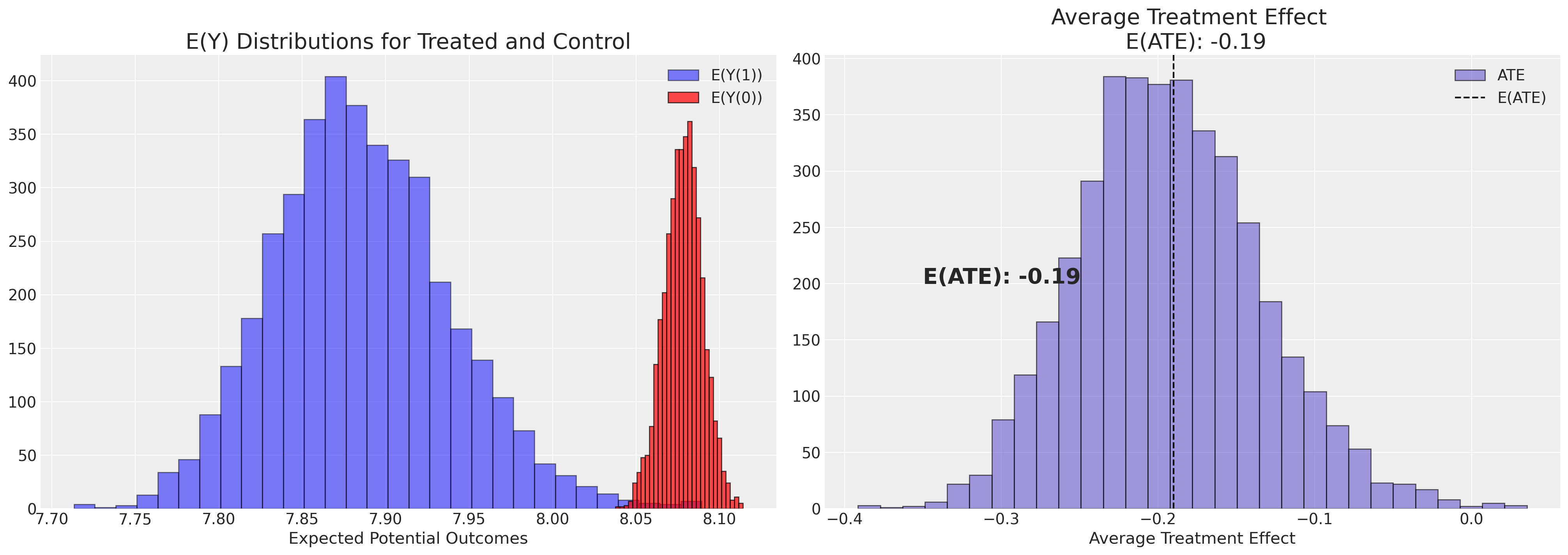
axs[1].set_title(f"Average Treatment Effect \n E(ATE): {ate}", fontsize=20)
axs[0].set_title("E(Y) Distributions for Treated and Control", fontsize=20)
axs[1].set_xlabel("Average Treatment Effect")
axs[0].set_xlabel("Expected Potential Outcomes")
axs[1].legend()
axs[0].legend()
plot_ate(ate_dist_df_logit)
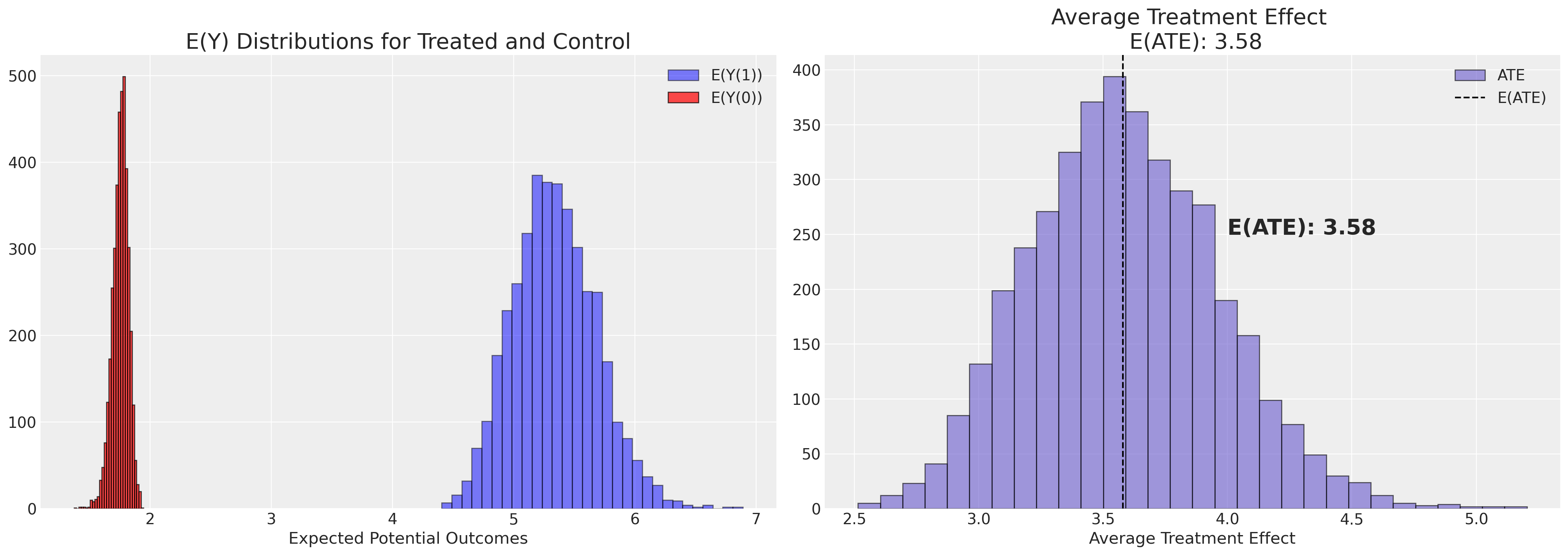
注意这个治疗效果的估计与我们通过简单地计算各组平均值的差异所得到的结果有很大的不同。
BART倾向模型#
接下来,我们将应用原始和对偶稳健估计器到使用BART非参数模型实现的倾向分布。
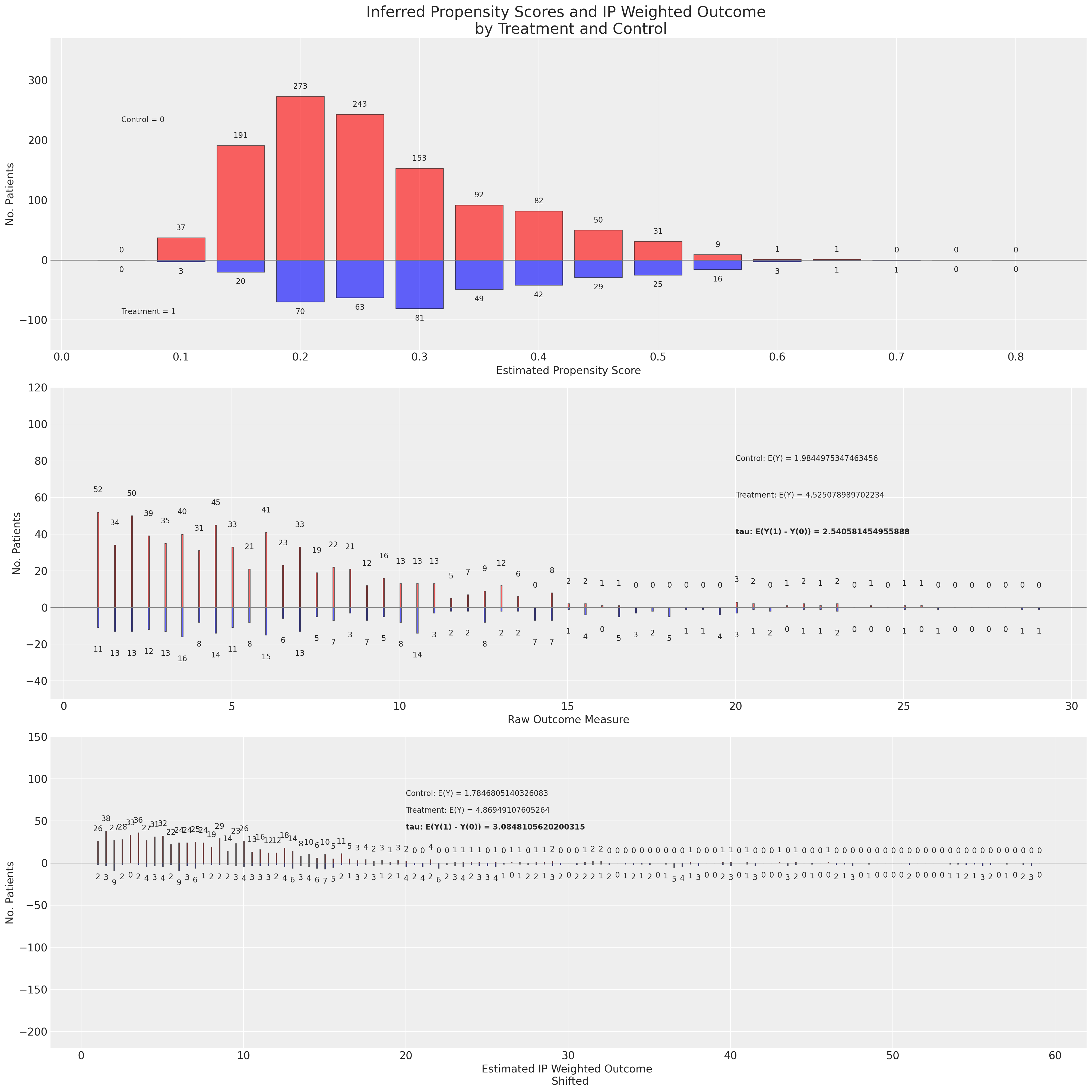
我们在这里看到,基于BART倾向得分的重加权方案如何使结果分布的形状与上述不同,但仍然实现了对ATE的相似估计。
ate_dist_probit = [get_ate(X, t, y, q, idata_probit, method="doubly_robust") for q in qs]
ate_dist_df_probit = pd.DataFrame(ate_dist_probit, columns=["ATE", "E(Y(1))", "E(Y(0))"])
ate_dist_df_probit.head()
| ATE | E(Y(1)) | E(Y(0)) | |
|---|---|---|---|
| 0 | 3.304293 | 5.088071 | 1.783777 |
| 1 | 3.416959 | 5.180571 | 1.763612 |
| 2 | 3.457275 | 5.229618 | 1.772343 |
| 3 | 3.531050 | 5.303977 | 1.772926 |
| 4 | 3.585944 | 5.345035 | 1.759090 |
plot_ate(ate_dist_df_probit, xy=(3.6, 250))
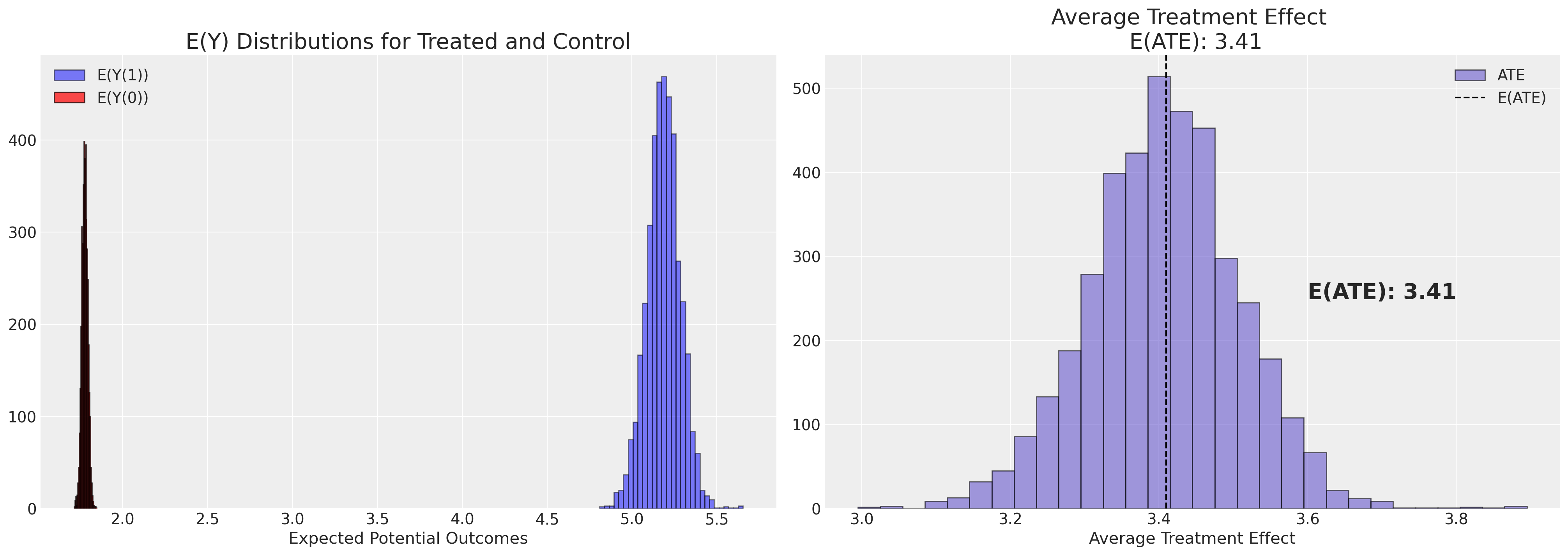
注意使用双重稳健方法测量的方差更小。这并不令人惊讶,因为双重稳健方法的设计初衷就是为了达到这种效果。
选择模型时的考虑因素#
评估整个人群的平均变化是一回事,但我们可能希望考虑到人群中效应异质性的概念,因此BART模型通常更擅长确保在我们数据的更深层级上进行准确的预测。但是,用于预测任务的机器学习模型的灵活性并不能保证在因果效应估计中使用的倾向得分在整个样本中是经过良好校准的,以恢复真实的治疗效果。我们必须谨慎地在因果背景下使用非参数模型的灵活性。
首先观察BART模型在我们样本中越来越窄的层中引起的异质性准确性。
Show code cell source
fig, axs = plt.subplots(4, 2, figsize=(20, 25))
axs = axs.flatten()
az.plot_ppc(idata_logit, ax=axs[0])
az.plot_ppc(idata_probit, ax=axs[1])
idx1 = list((X[X["race"] == 1].index).values)
idx0 = list((X[X["race"] == 0].index).values)
az.plot_ppc(idata_logit, ax=axs[2], coords={"obs": idx1})
az.plot_ppc(idata_probit, ax=axs[3], coords={"obs": idx0})
idx1 = list((X[(X["race"] == 1) & (X["sex"] == 1)].index).values)
idx0 = list((X[(X["race"] == 0) & (X["sex"] == 1)].index).values)
az.plot_ppc(idata_logit, ax=axs[4], coords={"obs": idx1})
az.plot_ppc(idata_probit, ax=axs[5], coords={"obs": idx0})
idx1 = list((X[(X["race"] == 1) & (X["sex"] == 1) & (X["active_1"] == 1)].index).values)
idx0 = list((X[(X["race"] == 0) & (X["sex"] == 1) & (X["active_1"] == 1)].index).values)
az.plot_ppc(idata_logit, ax=axs[6], coords={"obs": idx1})
az.plot_ppc(idata_probit, ax=axs[7], coords={"obs": idx0})
axs[0].set_title("Overall PPC - Logit")
axs[1].set_title("Overall PPC - BART")
axs[2].set_title("Race Specific PPC - Logit")
axs[3].set_title("Race Specific PPC - BART")
axs[4].set_title("Race/Gender Specific PPC - Logit")
axs[5].set_title("Race/Gender Specific PPC - BART")
axs[6].set_title("Race/Gender/Active Specific PPC - Logit")
axs[7].set_title("Race/Gender/Active Specific PPC - BART")
plt.suptitle("Posterior Predictive Checks - Heterogenous Effects", fontsize=20);
/Users/nathanielforde/mambaforge/envs/pymc_examples_new/lib/python3.9/site-packages/arviz/plots/ppcplot.py:267: FutureWarning: The return type of `Dataset.dims` will be changed to return a set of dimension names in future, in order to be more consistent with `DataArray.dims`. To access a mapping from dimension names to lengths, please use `Dataset.sizes`.
flatten_pp = list(predictive_dataset.dims.keys())
/Users/nathanielforde/mambaforge/envs/pymc_examples_new/lib/python3.9/site-packages/arviz/plots/ppcplot.py:271: FutureWarning: The return type of `Dataset.dims` will be changed to return a set of dimension names in future, in order to be more consistent with `DataArray.dims`. To access a mapping from dimension names to lengths, please use `Dataset.sizes`.
flatten = list(observed_data.dims.keys())

像这样的观察结果在推动在因果推断中使用灵活的机器学习方法方面起到了重要作用。用于捕捉结果分布或倾向得分分布的模型应当对数据极端值的变化敏感。我们可以看到,随着数据分区向下推进,简单逻辑回归模型的预测能力逐渐下降。下面我们将看到一个例子,其中像BART这样的机器学习模型的灵活性成为一个问题。我们还将看到如何解决这个问题。听起来可能有些矛盾,但更完美的倾向得分模型会清晰地分离处理类别,使得重新平衡变得更加困难。因此,在使用逆倾向加权方案时,像BART这样容易过拟合的灵活模型需要谨慎使用。
使用倾向评分进行回归#
另一种或许更直接的因果推断方法是使用回归分析。Angrist 和 Pischke Angrist 和 Pischke [2008] 认为回归的熟悉特性使其更具吸引力,但也承认倾向得分的作用,并指出谨慎的分析师可以将这些方法结合起来。在这里,我们将展示如何在回归背景下结合倾向得分来推导处理效应的估计值。
def make_prop_reg_model(X, t, y, idata_ps, covariates=None, samples=1000):
### Note the simplication for specifying the mean estimate in the regression
### rather than post-processing the whole posterior
ps = idata_ps["posterior"]["p"].mean(dim=("chain", "draw")).values
X_temp = pd.DataFrame({"ps": ps, "trt": t, "trt*ps": t * ps})
if covariates is None:
X = X_temp
else:
X = pd.concat([X_temp, X[covariates]], axis=1)
coords = {"coeffs": list(X.columns), "obs": range(len(X))}
with pm.Model(coords=coords) as model_ps_reg:
sigma = pm.HalfNormal("sigma", 1)
b = pm.Normal("b", mu=0, sigma=1, dims="coeffs")
X = pm.MutableData("X", X)
mu = pm.math.dot(X, b)
y_pred = pm.Normal("pred", mu, sigma, observed=y, dims="obs")
idata = pm.sample_prior_predictive()
idata.extend(pm.sample(samples, idata_kwargs={"log_likelihood": True}))
idata.extend(pm.sample_posterior_predictive(idata))
return model_ps_reg, idata
model_ps_reg, idata_ps_reg = make_prop_reg_model(X, t, y, idata_logit)
Sampling: [b, pred, sigma]
Auto-assigning NUTS sampler...
Initializing NUTS using jitter+adapt_diag...
Multiprocess sampling (4 chains in 4 jobs)
NUTS: [sigma, b]
Sampling 4 chains for 1_000 tune and 1_000 draw iterations (4_000 + 4_000 draws total) took 1 seconds.
Sampling: [pred]
使用倾向评分作为降维技术来拟合回归模型在这里似乎效果很好。我们恢复了与上述大致相同的处理效应估计。
az.summary(idata_ps_reg)
| mean | sd | hdi_3% | hdi_97% | mcse_mean | mcse_sd | ess_bulk | ess_tail | r_hat | |
|---|---|---|---|---|---|---|---|---|---|
| b[ps] | 2.450 | 0.614 | 1.330 | 3.663 | 0.010 | 0.007 | 3484.0 | 3083.0 | 1.0 |
| b[trt] | 3.473 | 0.482 | 2.575 | 4.376 | 0.009 | 0.006 | 2829.0 | 2664.0 | 1.0 |
| b[trt*ps] | -0.727 | 0.959 | -2.517 | 1.121 | 0.018 | 0.014 | 2900.0 | 2726.0 | 1.0 |
| sigma | 7.806 | 0.137 | 7.542 | 8.061 | 0.002 | 0.002 | 4139.0 | 2668.0 | 1.0 |
model_ps_reg_bart, idata_ps_reg_bart = make_prop_reg_model(X, t, y, idata_probit)
Sampling: [b, pred, sigma]
Auto-assigning NUTS sampler...
Initializing NUTS using jitter+adapt_diag...
Multiprocess sampling (4 chains in 4 jobs)
NUTS: [sigma, b]
Sampling 4 chains for 1_000 tune and 1_000 draw iterations (4_000 + 4_000 draws total) took 1 seconds.
Sampling: [pred]
az.summary(idata_ps_reg_bart)
| mean | sd | hdi_3% | hdi_97% | mcse_mean | mcse_sd | ess_bulk | ess_tail | r_hat | |
|---|---|---|---|---|---|---|---|---|---|
| b[ps] | 3.228 | 0.663 | 1.973 | 4.460 | 0.011 | 0.008 | 3568.0 | 2967.0 | 1.0 |
| b[trt] | 3.162 | 0.470 | 2.306 | 4.069 | 0.009 | 0.006 | 2859.0 | 2467.0 | 1.0 |
| b[trt*ps] | -0.301 | 0.954 | -2.038 | 1.554 | 0.017 | 0.013 | 3329.0 | 3087.0 | 1.0 |
| sigma | 7.780 | 0.133 | 7.532 | 8.028 | 0.002 | 0.001 | 4052.0 | 2978.0 | 1.0 |
因果推断作为回归插补#
上述内容中,我们将因果效应估计值读取为回归模型中处理变量的系数。一个可以说更干净的方法是使用拟合的回归模型来推算在不同处理制度下潜在结果Y(1)、Y(0)的分布。通过这种方式,我们对因果推断有了另一种视角。关键在于,这种视角是非参数化的,因为它不对推算模型所需的功能形式做出任何假设。
X_mod = X.copy()
X_mod["ps"] = ps = idata_probit["posterior"]["p"].mean(dim=("chain", "draw")).values
X_mod["trt"] = 1
X_mod["trt*ps"] = X_mod["ps"] * X_mod["trt"]
with model_ps_reg_bart:
# update values of predictors:
pm.set_data({"X": X_mod[["ps", "trt", "trt*ps"]]})
idata_trt = pm.sample_posterior_predictive(idata_ps_reg_bart)
idata_trt
Sampling: [pred]
-
<xarray.Dataset> Dimensions: (chain: 4, draw: 1000, obs: 1566) Coordinates: * chain (chain) int64 0 1 2 3 * draw (draw) int64 0 1 2 3 4 5 6 7 8 ... 992 993 994 995 996 997 998 999 * obs (obs) int64 0 1 2 3 4 5 6 7 ... 1559 1560 1561 1562 1563 1564 1565 Data variables: pred (chain, draw, obs) float64 -0.7491 0.1096 15.44 ... 3.267 0.2888 Attributes: created_at: 2024-02-24T19:03:12.138120 arviz_version: 0.17.0 inference_library: pymc inference_library_version: 5.3.0 -
<xarray.Dataset> Dimensions: (obs: 1566) Coordinates: * obs (obs) int64 0 1 2 3 4 5 6 7 ... 1559 1560 1561 1562 1563 1564 1565 Data variables: pred (obs) float64 -10.09 2.605 9.414 4.99 ... 1.36 3.515 4.763 15.76 Attributes: created_at: 2024-02-24T19:03:12.139483 arviz_version: 0.17.0 inference_library: pymc inference_library_version: 5.3.0 -
<xarray.Dataset> Dimensions: (X_dim_0: 1566, X_dim_1: 3) Coordinates: * X_dim_0 (X_dim_0) int64 0 1 2 3 4 5 6 ... 1560 1561 1562 1563 1564 1565 * X_dim_1 (X_dim_1) int64 0 1 2 Data variables: X (X_dim_0, X_dim_1) float64 0.1815 1.0 0.1815 ... 0.2776 1.0 0.2776 Attributes: created_at: 2024-02-24T19:03:12.140418 arviz_version: 0.17.0 inference_library: pymc inference_library_version: 5.3.0
X_mod = X.copy()
X_mod["ps"] = ps = idata_probit["posterior"]["p"].mean(dim=("chain", "draw")).values
X_mod["trt"] = 0
X_mod["trt*ps"] = X_mod["ps"] * X_mod["trt"]
with model_ps_reg_bart:
# update values of predictors:
pm.set_data({"X": X_mod[["ps", "trt", "trt*ps"]]})
idata_ntrt = pm.sample_posterior_predictive(idata_ps_reg_bart)
idata_ntrt
Sampling: [pred]
-
<xarray.Dataset> Dimensions: (chain: 4, draw: 1000, obs: 1566) Coordinates: * chain (chain) int64 0 1 2 3 * draw (draw) int64 0 1 2 3 4 5 6 7 8 ... 992 993 994 995 996 997 998 999 * obs (obs) int64 0 1 2 3 4 5 6 7 ... 1559 1560 1561 1562 1563 1564 1565 Data variables: pred (chain, draw, obs) float64 -13.99 5.743 -3.888 ... 3.793 -2.711 Attributes: created_at: 2024-02-24T19:03:12.404939 arviz_version: 0.17.0 inference_library: pymc inference_library_version: 5.3.0 -
<xarray.Dataset> Dimensions: (obs: 1566) Coordinates: * obs (obs) int64 0 1 2 3 4 5 6 7 ... 1559 1560 1561 1562 1563 1564 1565 Data variables: pred (obs) float64 -10.09 2.605 9.414 4.99 ... 1.36 3.515 4.763 15.76 Attributes: created_at: 2024-02-24T19:03:12.406164 arviz_version: 0.17.0 inference_library: pymc inference_library_version: 5.3.0 -
<xarray.Dataset> Dimensions: (X_dim_0: 1566, X_dim_1: 3) Coordinates: * X_dim_0 (X_dim_0) int64 0 1 2 3 4 5 6 ... 1560 1561 1562 1563 1564 1565 * X_dim_1 (X_dim_1) int64 0 1 2 Data variables: X (X_dim_0, X_dim_1) float64 0.1815 0.0 0.0 0.1758 ... 0.2776 0.0 0.0 Attributes: created_at: 2024-02-24T19:03:12.407083 arviz_version: 0.17.0 inference_library: pymc inference_library_version: 5.3.0
idata_trt["posterior_predictive"]["pred"].mean()
<xarray.DataArray 'pred' ()> array(3.91691031)
idata_ntrt["posterior_predictive"]["pred"].mean()
<xarray.DataArray 'pred' ()> array(0.82496553)
idata_trt["posterior_predictive"]["pred"].mean() - idata_ntrt["posterior_predictive"]["pred"].mean()
<xarray.DataArray 'pred' ()> array(3.09194478)
关于因果推断问题的所有这些观点在这里似乎都大致趋同。接下来我们将看到一个例子,其中分析师的选择可能会导致相当错误的结论,因此在应用这些推断工具时需要非常谨慎。
混杂推理:健康支出数据#
我们现在开始研究《贝叶斯非参数用于因果推断和缺失数据》中分析的健康支出数据集。这个数据集的一个显著特点是由于吸烟的存在,支出上没有明显的因果影响。我们遵循作者的思路,尝试对smoke对记录的log_y的影响进行建模。我们最初将重点放在估计ATE上。关于吸烟效果的信号很少。我们想展示即使我们选择了正确的方法,并尝试用正确的工具控制偏差,如果我们过于关注机制而忽视了数据生成过程,我们可能会错过眼前的故事。
try:
df = pd.read_csv("../data/meps_bayes_np_health.csv", index_col=["Unnamed: 0"])
except:
df = pd.read_csv(pm.get_data("meps_bayes_np_health.csv"), index_col=["Unnamed: 0"])
df = df[df["totexp"] > 0].reset_index(drop=True)
df["log_y"] = np.log(df["totexp"] + 1000)
df["loginc"] = np.log(df["income"])
df["smoke"] = np.where(df["smoke"] == "No", 0, 1)
df
/Users/nathanielforde/mambaforge/envs/pymc_examples_new/lib/python3.9/site-packages/pandas/core/arraylike.py:402: RuntimeWarning: divide by zero encountered in log
result = getattr(ufunc, method)(*inputs, **kwargs)
| age | bmi | edu | income | povlev | region | sex | marital | race | seatbelt | smoke | phealth | totexp | log_y | loginc | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 0 | 30 | 39.1 | 14 | 78400 | 343.69 | Northeast | Male | Married | White | Always | 0 | Fair | 40 | 6.946976 | 11.269579 |
| 1 | 53 | 20.2 | 17 | 180932 | 999.30 | West | Male | Married | Multi | Always | 0 | Very Good | 429 | 7.264730 | 12.105877 |
| 2 | 81 | 21.0 | 14 | 27999 | 205.94 | West | Male | Married | White | Always | 0 | Very Good | 14285 | 9.634627 | 10.239924 |
| 3 | 77 | 25.7 | 12 | 27999 | 205.94 | West | Female | Married | White | Always | 0 | Fair | 7959 | 9.100414 | 10.239924 |
| 4 | 31 | 23.0 | 12 | 14800 | 95.46 | South | Female | Divorced | White | Always | 0 | Excellent | 5017 | 8.702344 | 9.602382 |
| ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... |
| 16425 | 23 | 26.6 | 16 | 23000 | 130.72 | South | Male | Separated | Asian | Always | 0 | Very Good | 130 | 7.029973 | 10.043249 |
| 16426 | 55 | 21.9 | 12 | 23000 | 130.72 | South | Female | Married | Asian | Always | 0 | Very Good | 468 | 7.291656 | 10.043249 |
| 16427 | 22 | -9.0 | 9 | 7000 | 38.66 | Midwest | Male | Married | White | Always | 0 | Excellent | 711 | 7.444833 | 8.853665 |
| 16428 | 22 | 24.2 | 10 | 7000 | 38.66 | Midwest | Female | Married | White | Always | 0 | Excellent | 587 | 7.369601 | 8.853665 |
| 16429 | 20 | 26.9 | 10 | 9858 | 84.24 | Midwest | Female | Separated | White | Always | 0 | Fair | 1228 | 7.708860 | 9.196039 |
16430 行 × 15 列
汇总统计#
让我们回顾一下基本汇总统计数据,并看看它们在不同人口层中的变化
raw_diff = df.groupby("smoke")[["log_y"]].mean()
print("Treatment Diff:", raw_diff["log_y"].iloc[0] - raw_diff["log_y"].iloc[1])
raw_diff
Treatment Diff: 0.05280094075302166
| log_y | |
|---|---|
| smoke | |
| 0 | 8.098114 |
| 1 | 8.045313 |
pd.set_option("display.max_rows", 500)
strata_df = df.groupby(["smoke", "sex", "race", "phealth"])[["log_y"]].agg(["count", "mean", "std"])
global_avg = df["log_y"].mean()
strata_df["global_avg"] = global_avg
strata_df.reset_index(inplace=True)
strata_df.columns = [" ".join(col).strip() for col in strata_df.columns.values]
strata_df["diff"] = strata_df["log_y mean"] - strata_df["global_avg"]
strata_df.sort_values("log_y count", ascending=False).head(30).style.background_gradient(axis=0)
| smoke | sex | race | phealth | log_y count | log_y mean | log_y std | global_avg | diff | |
|---|---|---|---|---|---|---|---|---|---|
| 29 | 0 | Female | White | Very Good | 1858 | 8.101406 | 0.896128 | 8.089203 | 0.012204 |
| 27 | 0 | Female | White | Good | 1572 | 8.231117 | 1.010783 | 8.089203 | 0.141914 |
| 25 | 0 | Female | White | Excellent | 1385 | 7.919802 | 0.846725 | 8.089203 | -0.169400 |
| 59 | 0 | Male | White | Very Good | 1321 | 7.987652 | 0.922520 | 8.089203 | -0.101551 |
| 57 | 0 | Male | White | Good | 1129 | 8.178290 | 1.003363 | 8.089203 | 0.089088 |
| 55 | 0 | Male | White | Excellent | 1122 | 7.728966 | 0.779346 | 8.089203 | -0.360236 |
| 26 | 0 | Female | White | Fair | 659 | 8.487774 | 1.113656 | 8.089203 | 0.398572 |
| 7 | 0 | Female | Black | Good | 515 | 8.125243 | 0.944796 | 8.089203 | 0.036040 |
| 9 | 0 | Female | Black | Very Good | 488 | 7.870293 | 0.884956 | 8.089203 | -0.218909 |
| 56 | 0 | Male | White | Fair | 434 | 8.601018 | 1.112748 | 8.089203 | 0.511816 |
| 110 | 1 | Male | White | Good | 335 | 7.939632 | 0.887826 | 8.089203 | -0.149571 |
| 84 | 1 | Female | White | Good | 324 | 8.077777 | 0.968686 | 8.089203 | -0.011426 |
| 5 | 0 | Female | Black | Excellent | 307 | 7.748597 | 0.812461 | 8.089203 | -0.340606 |
| 6 | 0 | Female | Black | Fair | 266 | 8.534893 | 1.057159 | 8.089203 | 0.445690 |
| 86 | 1 | Female | White | Very Good | 266 | 7.913179 | 0.902211 | 8.089203 | -0.176024 |
| 39 | 0 | Male | Black | Very Good | 246 | 7.765843 | 0.831623 | 8.089203 | -0.323360 |
| 37 | 0 | Male | Black | Good | 235 | 8.002760 | 1.051284 | 8.089203 | -0.086443 |
| 112 | 1 | Male | White | Very Good | 235 | 7.848349 | 0.900002 | 8.089203 | -0.240854 |
| 4 | 0 | Female | Asian | Very Good | 193 | 7.864920 | 0.859187 | 8.089203 | -0.224283 |
| 83 | 1 | Female | White | Fair | 191 | 8.403307 | 0.989581 | 8.089203 | 0.314105 |
| 28 | 0 | Female | White | Poor | 186 | 9.160054 | 1.138894 | 8.089203 | 1.070852 |
| 35 | 0 | Male | Black | Excellent | 184 | 7.620076 | 0.771911 | 8.089203 | -0.469127 |
| 0 | 0 | Female | Asian | Excellent | 164 | 7.786508 | 0.899504 | 8.089203 | -0.302694 |
| 2 | 0 | Female | Asian | Good | 162 | 7.873122 | 0.768487 | 8.089203 | -0.216080 |
| 82 | 1 | Female | White | Excellent | 149 | 7.860320 | 0.837483 | 8.089203 | -0.228882 |
| 108 | 1 | Male | White | Excellent | 148 | 7.652529 | 0.717871 | 8.089203 | -0.436674 |
| 109 | 1 | Male | White | Fair | 148 | 8.282303 | 1.111403 | 8.089203 | 0.193101 |
| 58 | 0 | Male | White | Poor | 140 | 9.308711 | 1.255442 | 8.089203 | 1.219509 |
| 34 | 0 | Male | Asian | Very Good | 140 | 7.792831 | 0.772666 | 8.089203 | -0.296371 |
| 32 | 0 | Male | Asian | Good | 134 | 7.993583 | 1.123291 | 8.089203 | -0.095620 |
Show code cell source
def make_strata_plot(strata_df):
joined_df = strata_df[strata_df["smoke"] == 0].merge(
strata_df[strata_df["smoke"] == 1], on=["sex", "race", "phealth"]
)
joined_df.sort_values("diff_y", inplace=True)
# Func to draw line segment
def newline(p1, p2, color="black"):
ax = plt.gca()
l = mlines.Line2D([p1[0], p2[0]], [p1[1], p2[1]], color="black", linestyle="--")
ax.add_line(l)
return l
fig, ax = plt.subplots(figsize=(20, 15))
ax.scatter(
joined_df["diff_x"],
joined_df.index,
color="red",
alpha=0.7,
label="Control Sample Size",
s=joined_df["log_y count_x"] / 2,
)
ax.scatter(
joined_df["diff_y"],
joined_df.index,
color="blue",
alpha=0.7,
label="Treatment Sample Size",
s=joined_df["log_y count_y"] / 2,
)
for i, p1, p2 in zip(joined_df.index, joined_df["diff_x"], joined_df["diff_y"]):
newline([p1, i], [p2, i])
ax.set_xlabel("Difference from the Global Mean")
ax.set_title(
"Differences from Global Mean \n by Treatment Status and Strata",
fontsize=20,
fontweight="bold",
)
ax.axvline(0, color="k")
ax.set_ylabel("Strata Index")
ax.legend()
make_strata_plot(strata_df)
在这个可视化中很难看出一个清晰的规律。在两个治疗组中,当样本量较大时,我们发现两个组的平均差异都接近于零。
strata_expected_df = strata_df.groupby("smoke")[["log_y count", "log_y mean", "diff"]].agg(
{"log_y count": ["sum"], "log_y mean": "mean", "diff": "mean"}
)
print(
"Treatment Diff:",
strata_expected_df[("log_y mean", "mean")].iloc[0]
- strata_expected_df[("log_y mean", "mean")].iloc[1],
)
strata_expected_df
Treatment Diff: 0.28947855780477827
| log_y count | log_y mean | diff | |
|---|---|---|---|
| sum | mean | mean | |
| smoke | |||
| 0 | 13657 | 8.237595 | 0.148392 |
| 1 | 2773 | 7.948116 | -0.141087 |
确实,数据中似乎几乎没有受到我们治疗效果的影响。我们可以使用逆倾向评分加权的方法来恢复这一见解吗?
fig, axs = plt.subplots(2, 2, figsize=(20, 8))
axs = axs.flatten()
axs[0].hist(
df[df["smoke"] == 1]["log_y"],
alpha=0.3,
density=True,
bins=30,
label="Smoker",
ec="black",
color="blue",
)
axs[0].hist(
df[df["smoke"] == 0]["log_y"],
alpha=0.5,
density=True,
bins=30,
label="Non-Smoker",
ec="black",
color="red",
)
axs[1].hist(
df[df["smoke"] == 1]["log_y"],
density=True,
bins=30,
cumulative=True,
histtype="step",
label="Smoker",
color="blue",
)
axs[1].hist(
df[df["smoke"] == 0]["log_y"],
density=True,
bins=30,
cumulative=True,
histtype="step",
label="Non-Smoker",
color="red",
)
lkup = {1: "blue", 0: "red"}
axs[2].scatter(df["loginc"], df["log_y"], c=df["smoke"].map(lkup), alpha=0.4)
axs[2].set_xlabel("Log Income")
axs[3].scatter(df["age"], df["log_y"], c=df["smoke"].map(lkup), alpha=0.4)
axs[3].set_title("Log Outcome versus Age")
axs[2].set_title("Log Outcome versus Log Income")
axs[3].set_xlabel("Age")
axs[0].set_title("Empirical Densities")
axs[0].legend()
axs[1].legend()
axs[1].set_title("Empirical Cumulative \n Densities");
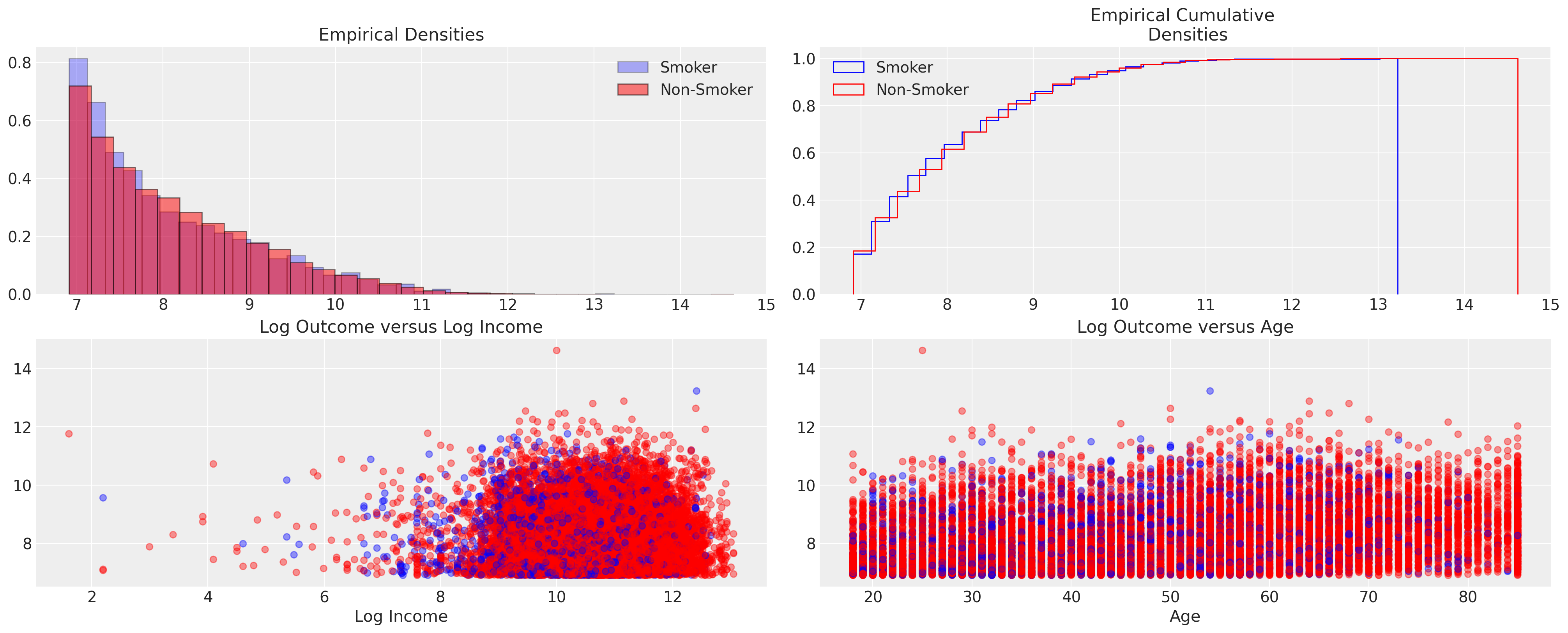
这些图表似乎证实了两个组之间结果的非差异化性质。在分布的外部分位数上存在一些差异的暗示。这一点很重要,因为它表明平均治疗效果最小。结果记录在对数美元尺度上,因此这里的任何单位变动都非常显著。
qs = np.linspace(0.05, 0.99, 100)
quantile_diff = (
df.groupby("smoke")[["totexp"]]
.quantile(qs)
.reset_index()
.pivot(index="level_1", columns="smoke", values="totexp")
.rename({0: "Non-Smoker", 1: "Smoker"}, axis=1)
.assign(diff=lambda x: x["Non-Smoker"] - x["Smoker"])
.reset_index()
.rename({"level_1": "quantile"}, axis=1)
)
fig, axs = plt.subplots(1, 2, figsize=(20, 6))
axs[0].plot(quantile_diff["quantile"], quantile_diff["Smoker"])
axs[0].plot(quantile_diff["quantile"], quantile_diff["Non-Smoker"])
axs[0].set_title("Q-Q plot comparing \n Smoker and Non-Smokers")
axs[1].plot(quantile_diff["quantile"], quantile_diff["diff"])
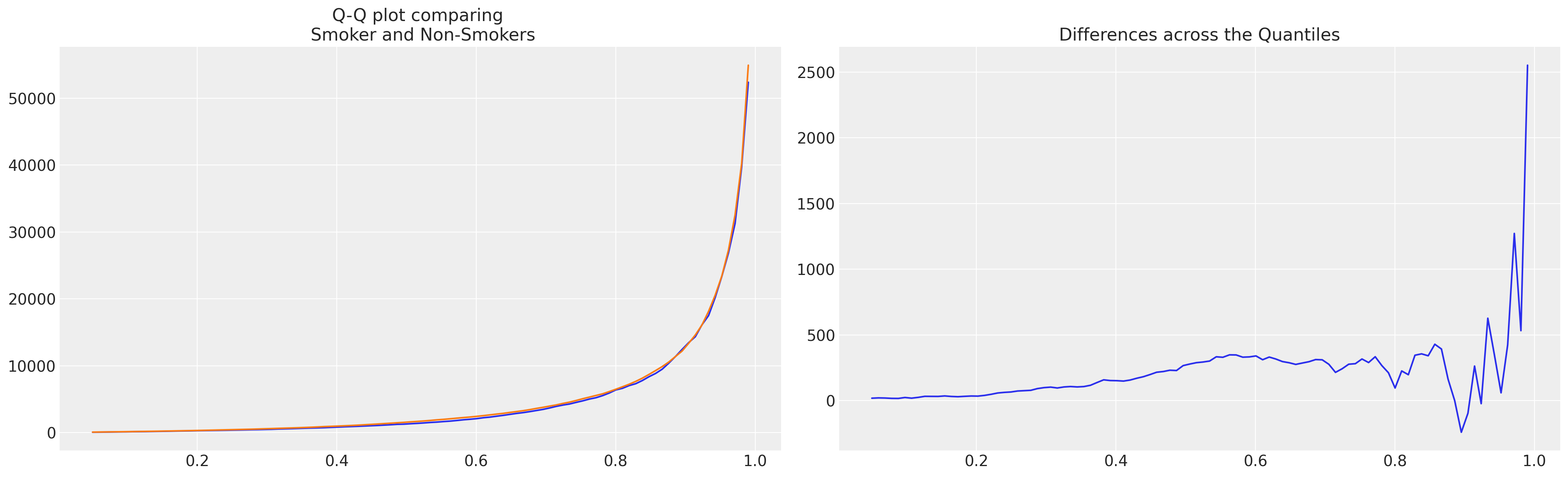
axs[1].set_title("Differences across the Quantiles");
可能会出什么问题?#
现在我们使用简单的虚拟编码来准备分类变量的数据,并从数据集中抽取一千个观测值用于我们的初始建模。
dummies = pd.concat(
[
pd.get_dummies(df["seatbelt"], drop_first=True, prefix="seatbelt"),
pd.get_dummies(df["marital"], drop_first=True, prefix="marital"),
pd.get_dummies(df["race"], drop_first=True, prefix="race"),
pd.get_dummies(df["sex"], drop_first=True, prefix="sex"),
pd.get_dummies(df["phealth"], drop_first=True, prefix="phealth"),
],
axis=1,
)
idx = df.sample(1000, random_state=100).index
X = pd.concat(
[
df[["age", "bmi"]],
dummies,
],
axis=1,
)
X = X.iloc[idx]
t = df.iloc[idx]["smoke"]
y = df.iloc[idx]["log_y"]
X
| age | bmi | seatbelt_Always | seatbelt_Never | seatbelt_NoCar | seatbelt_Seldom | seatbelt_Sometimes | marital_Married | marital_Separated | marital_Widowed | race_Black | race_Indig | race_Multi | race_PacificIslander | race_White | sex_Male | phealth_Fair | phealth_Good | phealth_Poor | phealth_Very Good | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 2852 | 27 | 23.7 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 1 | 0 | 0 | 0 | 0 |
| 13271 | 71 | 29.1 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 1 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 |
| 6786 | 19 | 21.3 | 1 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 1 |
| 15172 | 20 | 38.0 | 1 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 |
| 10967 | 22 | 28.7 | 1 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 1 |
| ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... |
| 5404 | 30 | 35.6 | 1 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 1 | 0 | 1 | 0 | 0 |
| 8665 | 80 | 22.0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 |
| 3726 | 49 | 32.9 | 1 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 1 | 0 | 1 | 0 | 0 |
| 6075 | 49 | 34.2 | 1 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 1 |
| 795 | 53 | 28.2 | 1 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 1 | 0 | 0 | 0 | 0 |
1000行 × 20列
m_ps_expend_bart, idata_expend_bart = make_propensity_model(
X, t, bart=True, probit=False, samples=1000, m=80
)
m_ps_expend_logit, idata_expend_logit = make_propensity_model(X, t, bart=False, samples=1000)
Sampling: [mu, t_pred]
Multiprocess sampling (4 chains in 4 jobs)
PGBART: [mu]
Sampling 4 chains for 1_000 tune and 1_000 draw iterations (4_000 + 4_000 draws total) took 46 seconds.
The rhat statistic is larger than 1.01 for some parameters. This indicates problems during sampling. See https://arxiv.org/abs/1903.08008 for details
The effective sample size per chain is smaller than 100 for some parameters. A higher number is needed for reliable rhat and ess computation. See https://arxiv.org/abs/1903.08008 for details
Sampling: [t_pred]
Sampling: [b, t_pred]
Auto-assigning NUTS sampler...
Initializing NUTS using jitter+adapt_diag...
Multiprocess sampling (4 chains in 4 jobs)
NUTS: [b]
Sampling 4 chains for 1_000 tune and 1_000 draw iterations (4_000 + 4_000 draws total) took 19 seconds.
Sampling: [t_pred]
az.plot_trace(idata_expend_bart, var_names=["mu", "p"]);
Show code cell source
ps = idata_expend_bart["posterior"]["p"].mean(dim=("chain", "draw")).values
fig, axs = plt.subplots(2, 1, figsize=(20, 10))
axs = axs.flatten()
ax = axs[0]
ax1 = axs[1]
ax1.set_title("Overlap of Inverted Propensity Scores")
ax.hist(
ps[t == 0],
bins=30,
ec="black",
alpha=0.4,
color="blue",
label="Propensity Scores in Treated",
)
ax1.hist(
ps[t == 0],
bins=30,
ec="black",
alpha=0.4,
color="blue",
label="Propensity Scores in Treated",
)
ax.set_xlabel("Propensity Scores")
ax.set_ylabel("Count of Observed")
ax1.set_ylabel("Count of Observed")
ax.hist(
ps[t == 1], bins=30, ec="black", alpha=0.6, color="red", label="Propensity Scores in Control"
)
ax1.hist(
1 - ps[t == 1],
bins=30,
ec="black",
alpha=0.6,
color="red",
label="Propensity Scores in Control",
)
ax.set_title("BART Model - Health Expenditure Data \n Propensity Scores per Group", fontsize=20)
ax.axvline(0.9, color="black", linestyle="--", label="Extreme Propensity Scores")
ax.axvline(0.1, color="black", linestyle="--")
ax1.axvline(0.9, color="black", linestyle="--", label="Extreme Propensity Scores")
ax1.axvline(0.1, color="black", linestyle="--")
ax.legend()
fig, ax2 = plt.subplots(figsize=(20, 6))
ax2.scatter(X["age"], y, color=t.map(colors), s=(1 / ps) * 20, ec="black", alpha=0.4)
ax2.set_xlabel("Age")
ax2.set_xlabel("Age")
ax2.set_ylabel("y")
ax2.set_ylabel("y")
ax2.set_title("Sized by IP Weights", fontsize=20)
red_patch = mpatches.Patch(color="red", label="Control")
blue_patch = mpatches.Patch(color="blue", label="Treated")
ax2.legend(handles=[red_patch, blue_patch]);
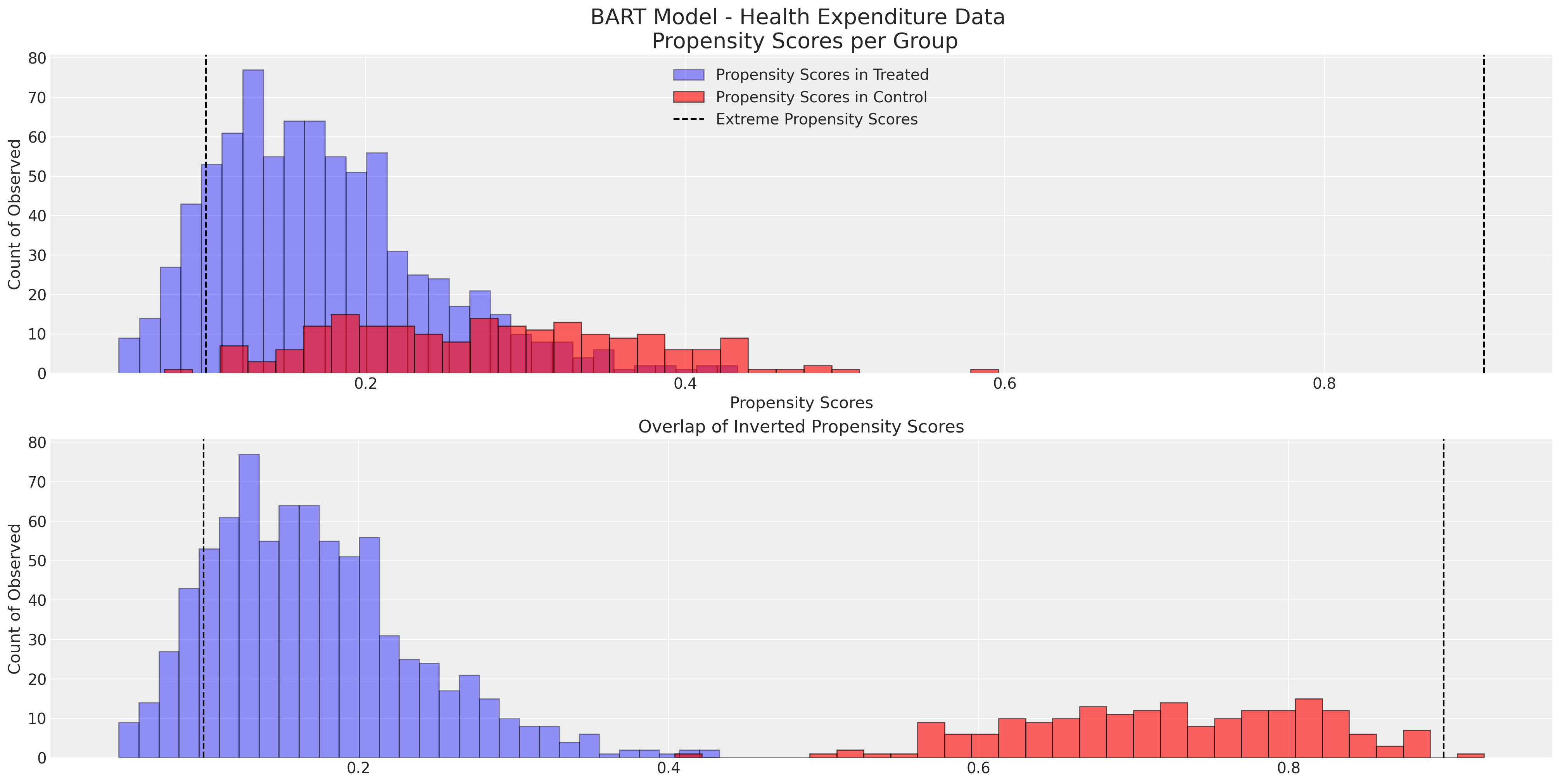
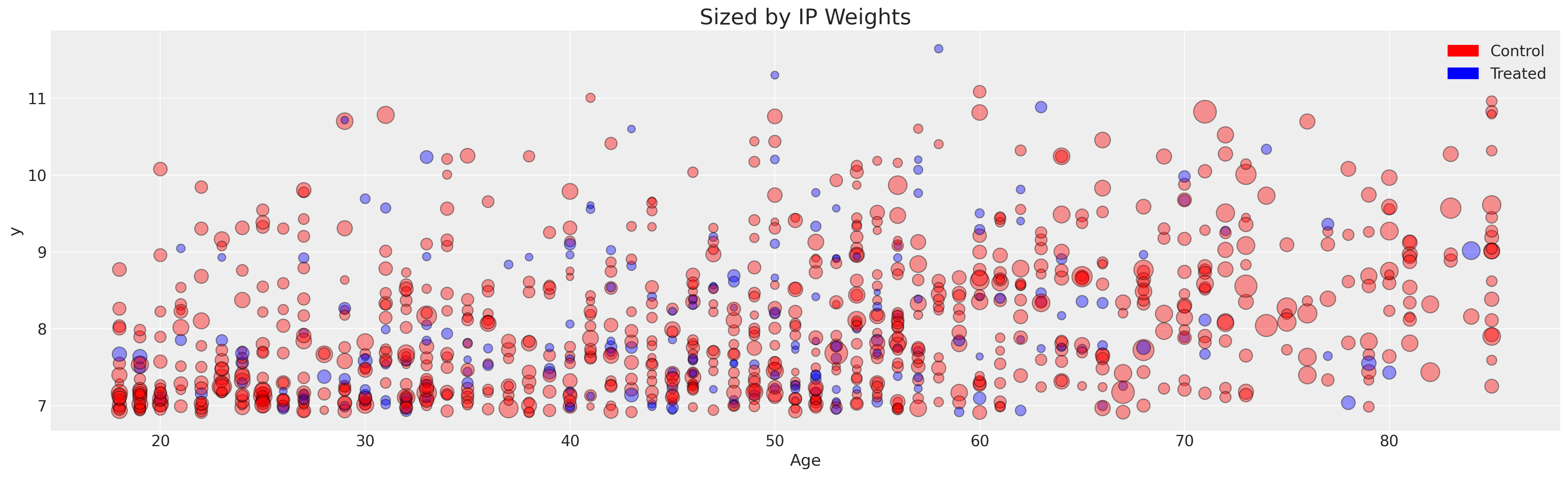
注意直方图中的每个组的尾部没有很好地重叠,并且我们有一些极端的倾向评分。这表明倾向评分可能没有很好地拟合,无法实现良好的平衡属性。
非参数BART倾向模型被错误指定#
BART模型的拟合灵活性校准不佳,无法恢复平均处理效应。让我们评估在鲁棒逆倾向权重估计下的加权结果分布。
## Evaluate at the expected realisation of the propensity scores for each individual
ps = idata_expend_bart["posterior"]["p"].mean(dim=("chain", "draw")).values
make_plot(
X,
idata_expend_bart,
ylims=[(-100, 340), (-60, 260), (-60, 260)],
lower_bins=[np.arange(6, 15, 0.5), np.arange(2, 14, 0.5)],
text_pos=(11, 80),
method="robust",
ps=ps,
)
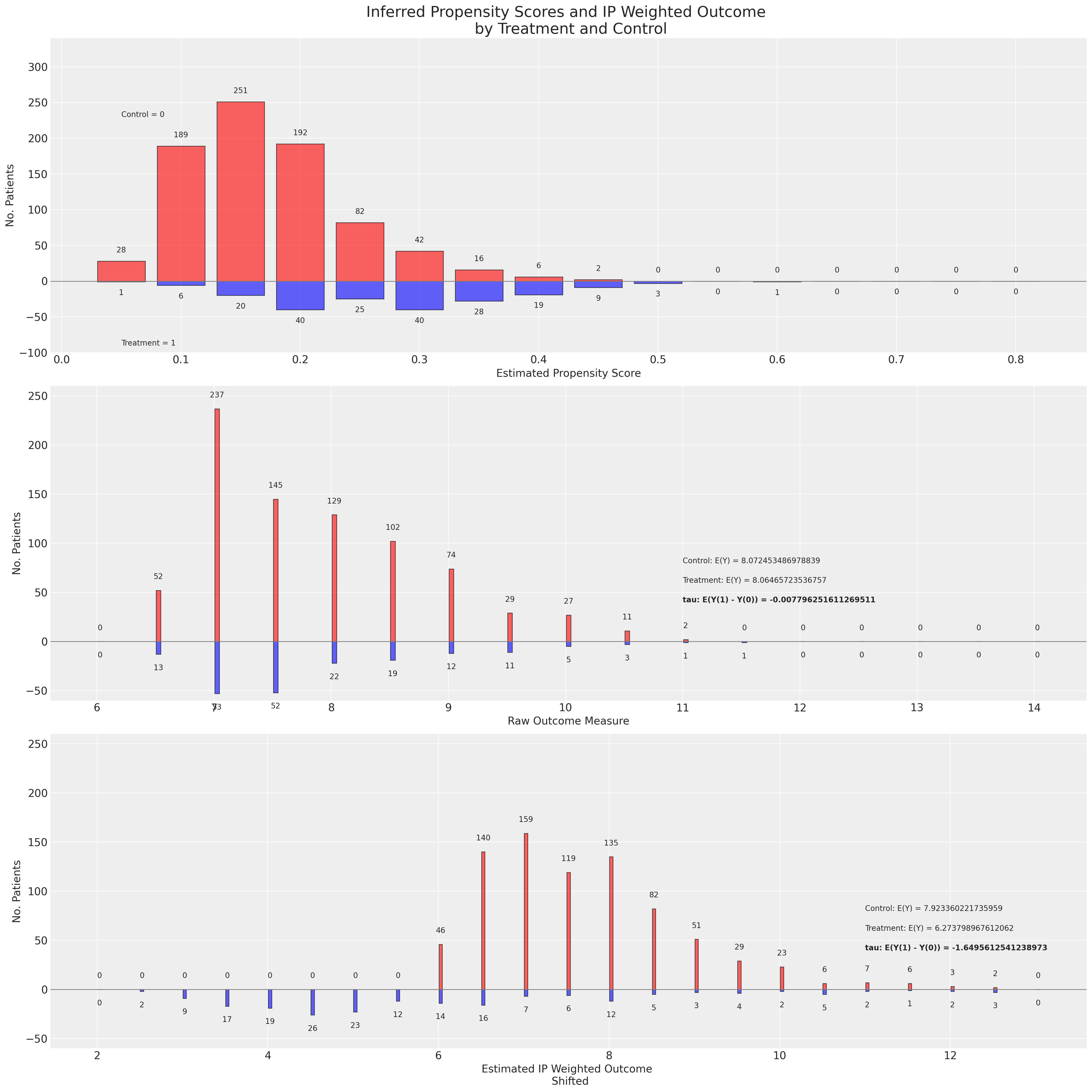
这是一个可疑的结果。在评估后倾向得分分布的预期值时,ATE的稳健IPW估计量表明处理组和对照组之间存在显著差异。第三面板中的重新加权结果在对照组和处理组之间出现分歧,表明平衡性严重失败。当原始结果的平均值的简单差异接近0时,但重新加权的差异在log尺度上显示出超过1的移动。这是怎么回事?接下来我们将从几个不同的角度来探讨这个问题,但你应该对这个结果持相当怀疑的态度。
如果我们查看不同估计量下的后验ATE分布会发生什么?
qs = range(4000)
ate_dist = [get_ate(X, t, y, q, idata_expend_bart, method="doubly_robust") for q in qs]
ate_dist_df_dr = pd.DataFrame(ate_dist, columns=["ATE", "E(Y(1))", "E(Y(0))"])
ate_dist = [get_ate(X, t, y, q, idata_expend_bart, method="robust") for q in qs]
ate_dist_df_r = pd.DataFrame(ate_dist, columns=["ATE", "E(Y(1))", "E(Y(0))"])
ate_dist_df_dr.head()
| ATE | E(Y(1)) | E(Y(0)) | |
|---|---|---|---|
| 0 | -0.240666 | 7.852410 | 8.093076 |
| 1 | -0.165757 | 7.920125 | 8.085882 |
| 2 | -0.104837 | 7.971139 | 8.075976 |
| 3 | -0.085442 | 7.992221 | 8.077663 |
| 4 | -0.122315 | 7.955486 | 8.077801 |
此表中的每一行显示了使用双重稳健估计器并从我们的BART模型拟合所隐含的倾向得分分布的后验中抽取的平均处理效果的估计值,以及结果变量的重新加权平均值。
plot_ate(ate_dist_df_r, xy=(0.5, 300))
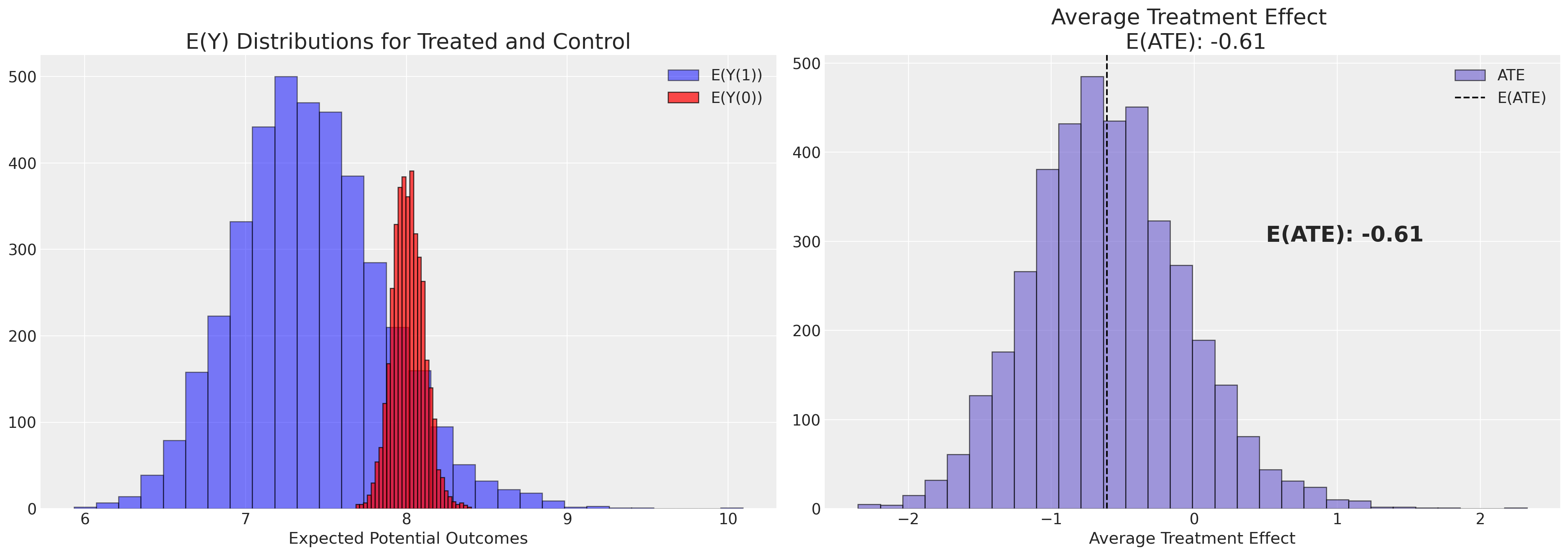
从后验分布的抽取中推导ATE估计值并对这些估计值进行平均,似乎给出了一个更合理的数值,但仍然超过了我们EDA所建议的最小差异。如果我们改用双重稳健估计器,我们再次得到了一个更合理的数值。
plot_ate(ate_dist_df_dr, xy=(-0.35, 200))
回想一下,双重稳健估计量旨在在倾向评分加权和(在我们的例子中)简单的OLS预测之间达成妥协。只要两个模型中的一个是正确指定的,这个估计量就可以恢复准确的无偏处理效果。在这种情况下,我们看到双重稳健估计量偏离了我们倾向评分的含义,并优先考虑回归模型。
我们还可以检查余额是否以及如何通过基于BART的倾向评分来分解,从而威胁到逆倾向评分加权的有效性。
temp = X.copy()
temp["ps"] = ps = idata_expend_bart["posterior"]["p"].mean(dim=("chain", "draw")).values
temp["ps_cut"] = pd.qcut(temp["ps"], 5)
plot_balance(temp, "bmi", t)
回归如何帮助?#
我们刚刚看到了一个例子,说明如果机器学习模型指定错误,如何会在研究中对因果估计产生极大的偏差。我们已经看到了一种解决方法,但如果我们尝试更简单的探索性回归建模,情况会如何呢?回归会根据数据点的协变量分布的极端程度及其在样本中的普遍性自动加权。因此,从这个意义上说,它以一种逆加权方法无法做到的方式调整了异常值倾向评分。
model_ps_reg_expend, idata_ps_reg_expend = make_prop_reg_model(X, t, y, idata_expend_bart)
Sampling: [b, pred, sigma]
Auto-assigning NUTS sampler...
Initializing NUTS using jitter+adapt_diag...
Multiprocess sampling (4 chains in 4 jobs)
NUTS: [sigma, b]
Sampling 4 chains for 1_000 tune and 1_000 draw iterations (4_000 + 4_000 draws total) took 1 seconds.
Sampling: [pred]
az.summary(idata_ps_reg_expend, var_names=["b"])
| mean | sd | hdi_3% | hdi_97% | mcse_mean | mcse_sd | ess_bulk | ess_tail | r_hat | |
|---|---|---|---|---|---|---|---|---|---|
| b[ps] | 25.533 | 0.774 | 23.977 | 26.884 | 0.016 | 0.011 | 2489.0 | 2640.0 | 1.0 |
| b[trt] | 1.393 | 0.386 | 0.670 | 2.118 | 0.008 | 0.005 | 2569.0 | 2348.0 | 1.0 |
| b[trt*ps] | -2.079 | 0.964 | -4.026 | -0.388 | 0.019 | 0.014 | 2588.0 | 2403.0 | 1.0 |
这个模型显然过于简单。它只能恢复由于误指定的BART倾向模型导致的偏差估计,但如果我们只是将倾向性作为我们协变量配置文件中的另一个特征呢?让它增加精度,但拟合我们认为真正反映因果关系的模型。
model_ps_reg_expend_h, idata_ps_reg_expend_h = make_prop_reg_model(
X,
t,
y,
idata_expend_bart,
covariates=["age", "bmi", "phealth_Fair", "phealth_Good", "phealth_Poor", "phealth_Very Good"],
)
Sampling: [b, pred, sigma]
Auto-assigning NUTS sampler...
Initializing NUTS using jitter+adapt_diag...
Multiprocess sampling (4 chains in 4 jobs)
NUTS: [sigma, b]
Sampling 4 chains for 1_000 tune and 1_000 draw iterations (4_000 + 4_000 draws total) took 3 seconds.
Sampling: [pred]
az.summary(idata_ps_reg_expend_h, var_names=["b"])
| mean | sd | hdi_3% | hdi_97% | mcse_mean | mcse_sd | ess_bulk | ess_tail | r_hat | |
|---|---|---|---|---|---|---|---|---|---|
| b[ps] | 8.799 | 0.588 | 7.759 | 9.963 | 0.010 | 0.007 | 3446.0 | 2897.0 | 1.0 |
| b[trt] | 0.098 | 0.245 | -0.364 | 0.553 | 0.004 | 0.004 | 3737.0 | 3063.0 | 1.0 |
| b[trt*ps] | -2.410 | 0.791 | -3.851 | -0.910 | 0.014 | 0.010 | 3392.0 | 2990.0 | 1.0 |
| b[age] | 0.065 | 0.002 | 0.061 | 0.070 | 0.000 | 0.000 | 3917.0 | 2809.0 | 1.0 |
| b[bmi] | 0.090 | 0.005 | 0.082 | 0.099 | 0.000 | 0.000 | 3688.0 | 2590.0 | 1.0 |
| b[phealth_Fair] | 0.285 | 0.180 | -0.051 | 0.625 | 0.003 | 0.002 | 3234.0 | 2768.0 | 1.0 |
| b[phealth_Good] | 0.409 | 0.149 | 0.150 | 0.701 | 0.003 | 0.002 | 2882.0 | 2797.0 | 1.0 |
| b[phealth_Poor] | 0.730 | 0.254 | 0.220 | 1.174 | 0.004 | 0.003 | 3532.0 | 2584.0 | 1.0 |
| b[phealth_Very Good] | 1.328 | 0.132 | 1.084 | 1.579 | 0.002 | 0.002 | 2975.0 | 2947.0 | 1.0 |
这要好得多,我们可以看到,将倾向评分特征与健康因素结合起来进行建模,可以得到一个更合理的治疗效果估计。这种发现呼应了Angrist和Pischke所报告的教训:
“回归控制正确的协变量可以合理地消除选择效应……” 第91页 基本无害的计量经济学 安格里斯特和皮施克 [2008]
因此,我们又回到了关于正确控制的问题上。没有真正的方法可以避免这一负担。机器学习在没有领域知识和对手头问题的仔细关注的情况下,不能作为万能药。这从来不是人们想听到的鼓舞人心的信息,但不幸的是,这是事实。回归分析对此有帮助,因为系数表的无情清晰提醒我们,没有比正确地测量事物更好的替代方法了。
双重/去偏机器学习与Frisch-Waugh-Lovell#
回顾一下 - 我们已经看到了两个使用逆概率加权调整进行因果推断的例子。我们看到了当倾向评分模型校准良好时它是如何起作用的。我们也看到了它何时失败以及如何修复这种失败。这些是我们工具箱中的工具 - 适用于不同的问题,但要求我们仔细思考数据生成过程和适当的协变量类型。
在简单倾向性建模方法失败的情况下,我们看到了一个数据集,其中我们的处理分配未能区分平均处理效应。我们还看到了如何通过增强基于倾向性的估计器来改善该技术的识别特性。在这里,我们将展示另一个例子,说明如何将倾向性模型与基于回归的建模中的见解结合起来,以利用机器学习方法在因果推断中提供的灵活建模可能性。在本节中,我们大量借鉴了Matheus Facure的工作,特别是他的书《Causal Inference in Python》Facure [2023],但原始想法可以在Victor et al. [2018]中找到
弗里施-沃夫-洛弗尔定理#
该定理的思想是,对于任何具有焦点参数 \(\beta_{1}\) 和辅助参数 \(\gamma_{i}\) 的 OLS 拟合线性模型
我们可以通过两步过程检索相同的值 \(\beta_{i}, \gamma_{i}\):
对辅助协变量进行回归,即 \(Y\) 在 \(\hat{Y} = \gamma_{1}Z_{1} + ... + \gamma_{n}Z_{n} \) 上
对 \(D_{1}\) 进行回归,使用相同的辅助项,即 \(\hat{D_{1}} = \gamma_{1}Z_{1} + ... + \gamma_{n}Z_{n}\)
取残差 \(r(D) = D_{1} - \hat{D_{1}}\) 和 \(r(Y) = Y - \hat{Y}\)
拟合回归 \(r(Y) = \beta_{0} + \beta_{1}r(D)\) 以找到 \(\beta_{1}\)
去偏机器学习的思想是复制这一过程,但在感兴趣的焦点变量是我们处理变量的情况下,利用机器学习模型的灵活性来估计两个残差项。
这与强可忽略性的要求密切相关,因为通过将焦点变量作为\(T\)使用此过程,我们创建了处理变量\(r(T)\),该变量通过构造无法从协变量配置文件\(X\)预测,从而确保\(T \perp\!\!\!\perp X\)。这是一个美妙的思想结合!
使用K折交叉验证避免过拟合#
正如我们上面所看到的,BART等基于树的模型自动正则化效果的一个问题是它们倾向于过度拟合已见数据。在这里,我们将使用K折交叉验证来生成对数据样本外部分的预测。这一步对于避免模型对样本数据的过度拟合至关重要,从而避免了我们上面看到的校准误差。这一点也很容易被遗忘,它是一个纠正步骤,以避免由于过度关注观察样本数据而导致的已知偏差。当我们估计特定样本的倾向得分时,使用倾向得分来实现平衡在过度拟合的情况下会失效。在这种情况下,我们的倾向模型过于符合样本的具体情况,无法在总体中起到相似性度量的作用。
dummies = pd.concat(
[
pd.get_dummies(df["seatbelt"], drop_first=True, prefix="seatbelt"),
pd.get_dummies(df["marital"], drop_first=True, prefix="marital"),
pd.get_dummies(df["race"], drop_first=True, prefix="race"),
pd.get_dummies(df["sex"], drop_first=True, prefix="sex"),
pd.get_dummies(df["phealth"], drop_first=True, prefix="phealth"),
],
axis=1,
)
train_dfs = []
temp = pd.concat([df[["age", "bmi"]], dummies], axis=1)
for i in range(4):
idx = temp.sample(1000, random_state=100).index
X = temp.iloc[idx].copy()
t = df.iloc[idx]["smoke"]
y = df.iloc[idx]["log_y"]
train_dfs.append([X, t, y])
remaining = [True if not i in idx else False for i in temp.index]
temp = temp[remaining]
temp.reset_index(inplace=True, drop=True)
应用去偏差机器学习方法#
接下来我们定义用于拟合和预测倾向得分模型和结果模型的函数。因为我们是贝叶斯方法,我们将记录结果模型和倾向模型残差的后验分布。在这两种情况下,我们都将使用基线BART规范,以利用机器学习的灵活性来提高准确性。然后,我们使用K折过程来拟合模型,并在样本外折叠上预测残差。这使我们能够通过后处理残差的后验预测分布来提取ATE的后验分布。
def train_outcome_model(X, y, m=50):
coords = {"coeffs": list(X.columns), "obs": range(len(X))}
with pm.Model(coords=coords) as model:
X_data = pm.MutableData("X", X)
y_data = pm.MutableData("y_data", y)
mu = pmb.BART("mu", X_data, y, m=m)
sigma = pm.HalfNormal("sigma", 1)
obs = pm.Normal("obs", mu, sigma, observed=y_data)
idata = pm.sample_prior_predictive()
idata.extend(pm.sample(1000, progressbar=False))
return model, idata
def train_propensity_model(X, t, m=50):
coords = {"coeffs": list(X.columns), "obs_id": range(len(X))}
with pm.Model(coords=coords) as model_ps:
X_data = pm.MutableData("X", X)
t_data = pm.MutableData("t_data", t)
mu = pmb.BART("mu", X_data, t, m=m)
p = pm.Deterministic("p", pm.math.invlogit(mu))
t_pred = pm.Bernoulli("obs", p=p, observed=t_data)
idata = pm.sample_prior_predictive()
idata.extend(pm.sample(1000, progressbar=False))
return model_ps, idata
def cross_validate(train_dfs, test_idx):
test = train_dfs[test_idx]
test_X = test[0]
test_t = test[1]
test_y = test[2]
train_X = pd.concat([train_dfs[i][0] for i in range(4) if i != test_idx])
train_t = pd.concat([train_dfs[i][1] for i in range(4) if i != test_idx])
train_y = pd.concat([train_dfs[i][2] for i in range(4) if i != test_idx])
model, idata = train_outcome_model(train_X, train_y)
with model:
pm.set_data({"X": test_X, "y_data": test_y})
idata_pred = pm.sample_posterior_predictive(idata)
y_resid = idata_pred["posterior_predictive"]["obs"].stack(z=("chain", "draw")).T - test_y.values
model_t, idata_t = train_propensity_model(train_X, train_t)
with model_t:
pm.set_data({"X": test_X, "t_data": test_t})
idata_pred_t = pm.sample_posterior_predictive(idata_t)
t_resid = (
idata_pred_t["posterior_predictive"]["obs"].stack(z=("chain", "draw")).T - test_t.values
)
return y_resid, t_resid, idata_pred, idata_pred_t
y_resids = []
t_resids = []
model_fits = {}
for i in range(4):
y_resid, t_resid, idata_pred, idata_pred_t = cross_validate(train_dfs, i)
y_resids.append(y_resid)
t_resids.append(t_resid)
t_effects = []
for j in range(1000):
intercept = np.ones_like(1000)
covariates = pd.DataFrame({"intercept": intercept, "t_resid": t_resid[j, :].values})
m0 = sm.OLS(y_resid[j, :].values, covariates).fit()
t_effects.append(m0.params["t_resid"])
model_fits[i] = [m0, t_effects]
print(f"Estimated Treament Effect in K-fold {i}: {np.mean(t_effects)}")
Show code cell output
Sampling: [mu, obs, sigma]
Multiprocess sampling (4 chains in 4 jobs)
CompoundStep
>PGBART: [mu]
>NUTS: [sigma]
Sampling 4 chains for 1_000 tune and 1_000 draw iterations (4_000 + 4_000 draws total) took 31 seconds.
The rhat statistic is larger than 1.01 for some parameters. This indicates problems during sampling. See https://arxiv.org/abs/1903.08008 for details
The effective sample size per chain is smaller than 100 for some parameters. A higher number is needed for reliable rhat and ess computation. See https://arxiv.org/abs/1903.08008 for details
Sampling: [mu, obs]
Sampling: [mu, obs]
Multiprocess sampling (4 chains in 4 jobs)
PGBART: [mu]
Sampling 4 chains for 1_000 tune and 1_000 draw iterations (4_000 + 4_000 draws total) took 51 seconds.
The rhat statistic is larger than 1.01 for some parameters. This indicates problems during sampling. See https://arxiv.org/abs/1903.08008 for details
The effective sample size per chain is smaller than 100 for some parameters. A higher number is needed for reliable rhat and ess computation. See https://arxiv.org/abs/1903.08008 for details
Sampling: [mu, obs]
Estimated Treament Effect in K-fold 0: -0.007055724114450991
Sampling: [mu, obs, sigma]
Multiprocess sampling (4 chains in 4 jobs)
CompoundStep
>PGBART: [mu]
>NUTS: [sigma]
Sampling 4 chains for 1_000 tune and 1_000 draw iterations (4_000 + 4_000 draws total) took 31 seconds.
The rhat statistic is larger than 1.01 for some parameters. This indicates problems during sampling. See https://arxiv.org/abs/1903.08008 for details
The effective sample size per chain is smaller than 100 for some parameters. A higher number is needed for reliable rhat and ess computation. See https://arxiv.org/abs/1903.08008 for details
Sampling: [mu, obs]
Sampling: [mu, obs]
Multiprocess sampling (4 chains in 4 jobs)
PGBART: [mu]
Sampling 4 chains for 1_000 tune and 1_000 draw iterations (4_000 + 4_000 draws total) took 50 seconds.
The rhat statistic is larger than 1.01 for some parameters. This indicates problems during sampling. See https://arxiv.org/abs/1903.08008 for details
The effective sample size per chain is smaller than 100 for some parameters. A higher number is needed for reliable rhat and ess computation. See https://arxiv.org/abs/1903.08008 for details
Sampling: [mu, obs]
Estimated Treament Effect in K-fold 1: -0.0381788005862483
Sampling: [mu, obs, sigma]
Multiprocess sampling (4 chains in 4 jobs)
CompoundStep
>PGBART: [mu]
>NUTS: [sigma]
Sampling 4 chains for 1_000 tune and 1_000 draw iterations (4_000 + 4_000 draws total) took 31 seconds.
The rhat statistic is larger than 1.01 for some parameters. This indicates problems during sampling. See https://arxiv.org/abs/1903.08008 for details
The effective sample size per chain is smaller than 100 for some parameters. A higher number is needed for reliable rhat and ess computation. See https://arxiv.org/abs/1903.08008 for details
Sampling: [mu, obs]
Sampling: [mu, obs]
Multiprocess sampling (4 chains in 4 jobs)
PGBART: [mu]
Sampling 4 chains for 1_000 tune and 1_000 draw iterations (4_000 + 4_000 draws total) took 50 seconds.
The rhat statistic is larger than 1.01 for some parameters. This indicates problems during sampling. See https://arxiv.org/abs/1903.08008 for details
The effective sample size per chain is smaller than 100 for some parameters. A higher number is needed for reliable rhat and ess computation. See https://arxiv.org/abs/1903.08008 for details
Sampling: [mu, obs]
Estimated Treament Effect in K-fold 2: -0.03088459747780483
Sampling: [mu, obs, sigma]
Multiprocess sampling (4 chains in 4 jobs)
CompoundStep
>PGBART: [mu]
>NUTS: [sigma]
Sampling 4 chains for 1_000 tune and 1_000 draw iterations (4_000 + 4_000 draws total) took 31 seconds.
The rhat statistic is larger than 1.01 for some parameters. This indicates problems during sampling. See https://arxiv.org/abs/1903.08008 for details
The effective sample size per chain is smaller than 100 for some parameters. A higher number is needed for reliable rhat and ess computation. See https://arxiv.org/abs/1903.08008 for details
Sampling: [mu, obs]
Sampling: [mu, obs]
Multiprocess sampling (4 chains in 4 jobs)
PGBART: [mu]
Sampling 4 chains for 1_000 tune and 1_000 draw iterations (4_000 + 4_000 draws total) took 51 seconds.
The rhat statistic is larger than 1.01 for some parameters. This indicates problems during sampling. See https://arxiv.org/abs/1903.08008 for details
The effective sample size per chain is smaller than 100 for some parameters. A higher number is needed for reliable rhat and ess computation. See https://arxiv.org/abs/1903.08008 for details
Sampling: [mu, obs]
Estimated Treament Effect in K-fold 3: 0.0012725964211934963
<xarray.DataArray 'obs' (z: 4000, obs_dim_2: 4000)>
array([[ 2.12096806, -0.18759006, 1.65643341, ..., 0.96914617,
-1.09227918, 0.79439211],
[-0.2475453 , -1.71716078, 0.90773827, ..., 1.9150216 ,
0.22575749, 1.205472 ],
[ 1.84052802, -0.06495813, 1.13329414, ..., 0.33619207,
-0.97017944, 1.55807636],
...,
[ 1.11205571, 0.00451481, -0.11181589, ..., 3.16765911,
-1.85359818, 1.12836815],
[ 0.60629988, 0.96163265, 1.32810649, ..., 1.97479916,
-0.09903109, 1.37666937],
[ 0.52163258, -0.11855604, -0.28945473, ..., 0.24204002,
-0.6780746 , 0.18923211]])
Coordinates:
* obs_dim_2 (obs_dim_2) int64 0 1 2 3 4 5 6 7 ... 993 994 995 996 997 998 999
* z (z) object MultiIndex
* chain (z) int64 0 0 0 0 0 0 0 0 0 0 0 0 0 ... 3 3 3 3 3 3 3 3 3 3 3 3 3
* draw (z) int64 0 1 2 3 4 5 6 7 8 ... 992 993 994 995 996 997 998 999后处理残差的后验预测分布
t_effects = []
intercepts = []
for i in range(4000):
intercept = np.ones_like(4000)
covariates = pd.DataFrame({"intercept": intercept, "t_resid": t_resids_stacked[i, :].values})
m0 = sm.OLS(y_resids_stacked[i, :].values, covariates).fit()
t_effects.append(m0.params["t_resid"])
intercepts.append(m0.params["intercept"])
fig, axs = plt.subplots(1, 2, figsize=(15, 6))
axs = axs.flatten()
axs[0].hist(t_effects, bins=30, ec="black", color="slateblue", label="ATE", density=True, alpha=0.6)
x = np.linspace(-1, 1, 10)
for i in range(1000):
axs[1].plot(x, intercepts[i] + t_effects[i] * x, color="darkred", alpha=0.3)
axs[0].set_title("Double ML - ATE estimate \n Distribution")
axs[1].set_title(r" Posterior Regression Line of Residuals: r(Y) ~ $\beta$r(T)")
ate = np.mean(t_effects)
axs[0].axvline(ate, color="black", linestyle="--", label=f"E(ATE) = {np.round(ate, 2)}")
axs[1].plot(x, np.mean(intercepts) + np.mean(t_effects) * x, color="black", label="Expected Fit")
axs[1].legend()
axs[0].legend();
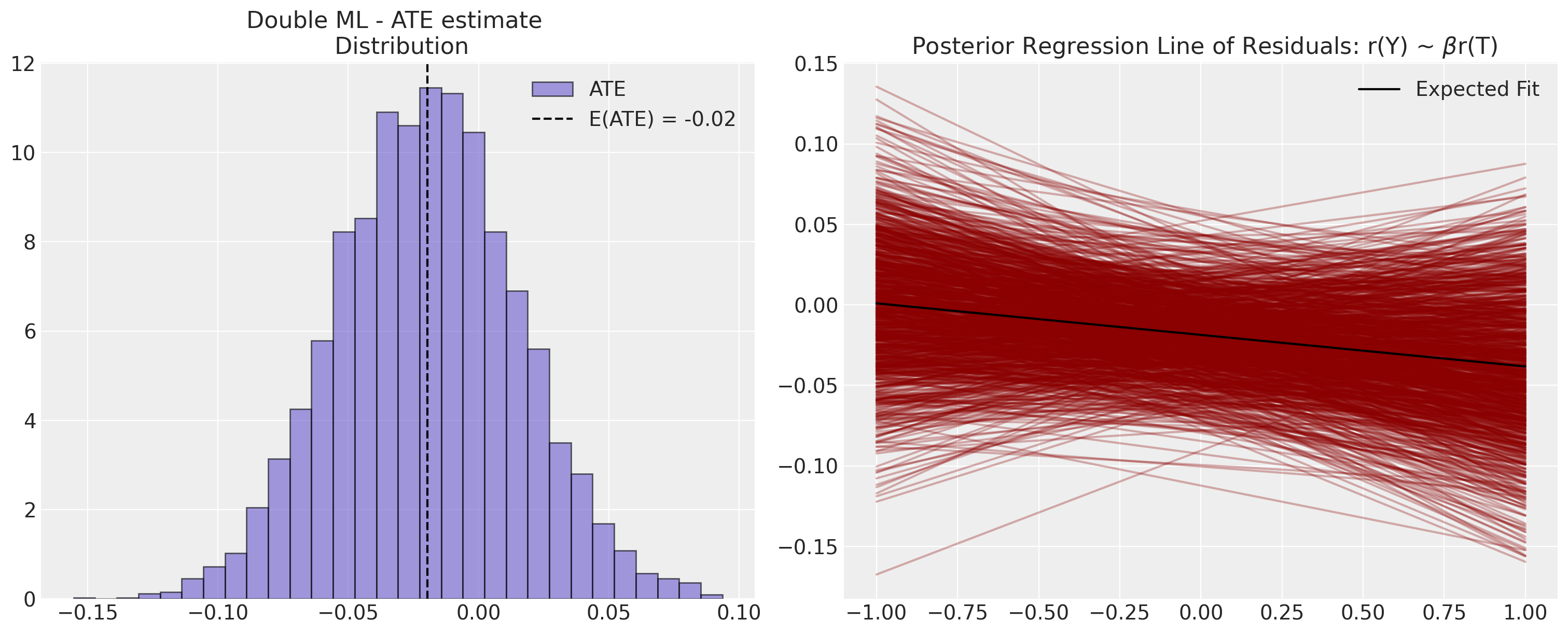
我们可以看到,去偏机器学习技术如何帮助缓解了将BART模型天真地拟合到倾向得分估计任务中的一些校准不当的影响。此外,我们现在量化了ATE中的一些不确定性,这决定了残差上的相对平坦的回归线。
条件平均处理效应#
我们在这里指出,双重机器学习方法也为这个问题提供了另一种视角。它们使你能够摆脱对平均处理效应的关注,并获得更符合个体协变量特征的估计。大部分理论细节在Facure [2023]中有详细阐述,我们在这里除了建议在估计特定处理效应时使用残差预测是合理的之外,不会详细讨论。我们将简要展示如何基于导出的残差,利用机器学习的灵活性来更好地捕捉异质处理效应的范围,从而获得条件平均处理效应(CATE)的估计。
def make_cate(y_resids_stacked, t_resids_stacked, train_dfs, i, method="forest"):
train_X = pd.concat([train_dfs[i][0] for i in range(4)])
train_t = pd.concat([train_dfs[i][1] for i in range(4)])
df_cate = pd.DataFrame(
{"y_r": y_resids_stacked[i, :].values, "t_r": t_resids_stacked[i, :].values}
)
df_cate["target"] = df_cate["y_r"] / np.where(
df_cate["t_r"] == 0, df_cate["t_r"] + 1e-25, df_cate["t_r"]
)
df_cate["weight"] = df_cate["t_r"] ** 2
train_X.reset_index(drop=True, inplace=True)
train_t.reset_index(drop=True, inplace=True)
if method == "forest":
CATE_model = RandomForestRegressor()
CATE_model.fit(train_X, df_cate["target"], sample_weight=df_cate["weight"])
elif method == "gradient":
CATE_model = GradientBoostingRegressor()
CATE_model.fit(train_X, df_cate["target"], sample_weight=df_cate["weight"])
else:
CATE_model = sm.WLS(df_cate["target"], train_X, weights=df_cate["weight"])
CATE_model = CATE_model.fit()
df_cate["CATE"] = CATE_model.predict(train_X)
df_cate["t"] = train_t
return df_cate
Show code cell source
fig, axs = plt.subplots(1, 3, figsize=(20, 7))
axs = axs.flatten()
q_95 = []
for i in range(100):
cate_df = make_cate(y_resids_stacked, t_resids_stacked, train_dfs, i)
axs[1].hist(
cate_df[cate_df["t"] == 0]["CATE"],
bins=30,
alpha=0.1,
color="red",
density=True,
)
q_95.append(
[
cate_df[cate_df["t"] == 0]["CATE"].quantile(0.99),
cate_df[cate_df["t"] == 1]["CATE"].quantile(0.99),
cate_df[cate_df["t"] == 0]["CATE"].quantile(0.01),
cate_df[cate_df["t"] == 1]["CATE"].quantile(0.01),
]
)
axs[1].hist(cate_df[cate_df["t"] == 1]["CATE"], bins=30, alpha=0.1, color="blue", density=True)
axs[1].set_title(
"CATE Predictions \n Estimated across Posterior of Residuals", fontsize=20, fontweight="bold"
)
q_df = pd.DataFrame(q_95, columns=["Control_p99", "Treated_p99", "Control_p01", "Treated_p01"])
axs[2].hist(q_df["Treated_p99"], ec="black", color="blue", alpha=0.4, label="Treated p99")
axs[2].hist(q_df["Control_p99"], ec="black", color="red", alpha=0.4, label="Control p99")
axs[2].legend()
axs[2].set_title("Distribution of p99 CATE predictions")
axs[0].hist(q_df["Treated_p01"], ec="black", color="blue", alpha=0.4, label="Treated p01")
axs[0].hist(q_df["Control_p01"], ec="black", color="red", alpha=0.4, label="Control p01")
axs[0].legend()
axs[0].set_title("Distribution of p01 CATE predictions");
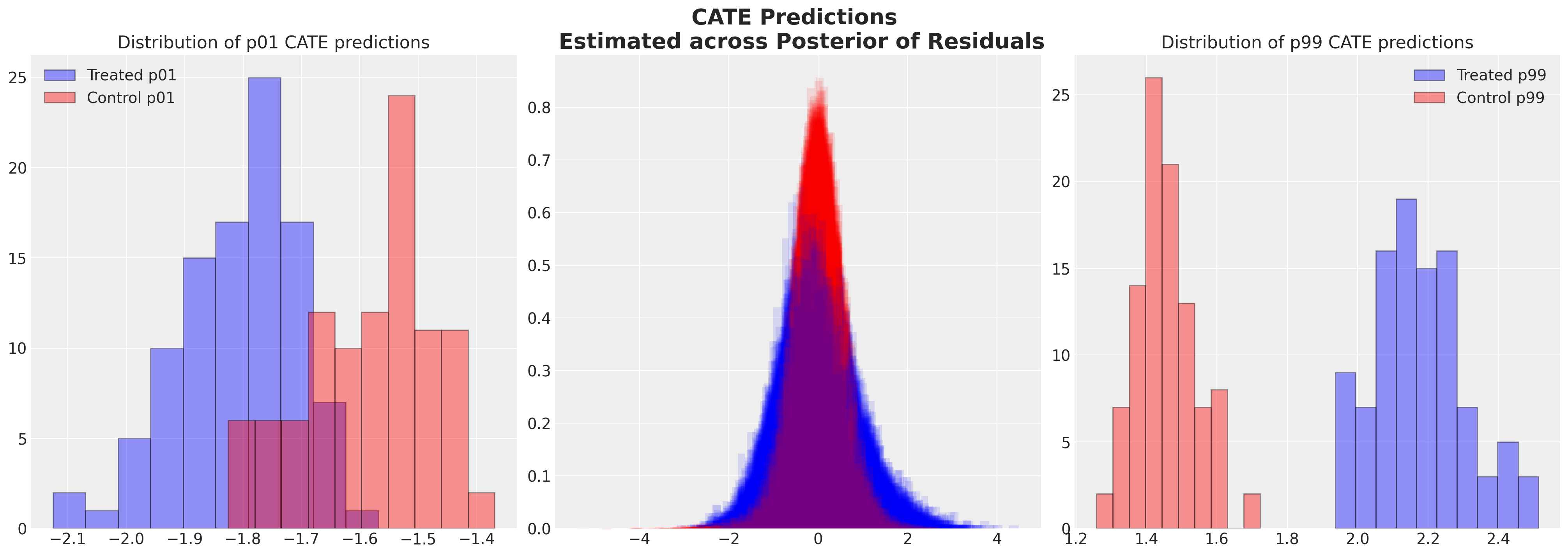
这种观点开始显示出因果影响中异质性的重要性,并提供了一种评估治疗差异影响的方法。然而,尽管接受治疗的人群(即吸烟者)被暗示具有更长的尾部和更极端的结果——你可能会想知道为什么这种影响在某种程度上是对称的?为什么他们也会表现出较不极端的支出呢?
中介效应与因果结构#
上面我们已经看到,许多旨在避免偏见的方法使我们得出结论:吸烟对您的医疗保健费用影响有限或没有影响。值得强调的是,这应该让您感到奇怪!
这个谜题的答案并不在于精确的估计方法,而在于问题的结构。并不是说吸烟与医疗成本无关,而是吸烟对医疗成本的影响是通过其对健康的影响来实现的。
中介的结构要求有效的因果推断必须在中介的结构下进行,即当序列可忽略性成立时。也就是说——潜在结果在给定协变量配置的情况下,与处理分配历史无关。更多细节可以在Daniels et al. [2024]中找到。但如果我们将中介结构写入我们的模型中,如贝叶斯中介分析中所述,我们可以看到这是如何工作的。关键点在于我们需要增强我们的建模,以考虑因果流的结构。这是我们对数据生成过程的实质性结构信念,我们在中介和结果的联合分布模型中施加这种信念。
fig, ax = plt.subplots(figsize=(20, 6))
graph = nx.DiGraph()
graph.add_node("T")
graph.add_node("M")
graph.add_node("Y")
graph.add_edges_from([("T", "M"), ("M", "Y"), ("T", "Y")])
nx.draw(
graph,
arrows=True,
with_labels=True,
pos={"T": (1, 2), "M": (1.8, 3), "Y": (3, 1)},
ax=ax,
node_size=6000,
font_color="whitesmoke",
font_size=20,
)
这里,处理T通过中介M影响结果Y,同时直接对结果产生影响。
dummies = pd.concat(
[
pd.get_dummies(df["seatbelt"], drop_first=True, prefix="seatbelt"),
pd.get_dummies(df["marital"], drop_first=True, prefix="marital"),
pd.get_dummies(df["race"], drop_first=True, prefix="race"),
pd.get_dummies(df["sex"], drop_first=True, prefix="sex"),
pd.get_dummies(df["phealth"], drop_first=True, prefix="phealth"),
],
axis=1,
)
idx = df.sample(5000, random_state=100).index
X = pd.concat(
[
df[["age", "bmi"]],
dummies,
],
axis=1,
)
X = X.iloc[idx]
t = df.iloc[idx]["smoke"]
y = df.iloc[idx]["log_y"]
X
lkup = {
"phealth_Poor": 1,
"phealth_Fair": 2,
"phealth_Good": 3,
"phealth_Very Good": 4,
"phealth_Excellent": 5,
}
### Construct the health status variables as an ordinal rank
### to use the health rank as a mediator for smoking.
m = pd.DataFrame(
(
pd.from_dummies(
X[["phealth_Poor", "phealth_Fair", "phealth_Good", "phealth_Very Good"]],
default_category="phealth_Excellent",
).values.flatten()
),
columns=["health"],
)["health"].map(lkup)
X_m = X.copy().drop(["phealth_Poor", "phealth_Fair", "phealth_Good", "phealth_Very Good"], axis=1)
X_m
| age | bmi | seatbelt_Always | seatbelt_Never | seatbelt_NoCar | seatbelt_Seldom | seatbelt_Sometimes | marital_Married | marital_Separated | marital_Widowed | race_Black | race_Indig | race_Multi | race_PacificIslander | race_White | sex_Male | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 2852 | 27 | 23.7 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 1 |
| 13271 | 71 | 29.1 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 1 | 0 | 0 | 0 | 0 | 0 |
| 6786 | 19 | 21.3 | 1 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 1 | 0 |
| 15172 | 20 | 38.0 | 1 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 1 | 0 | 0 | 0 | 0 | 0 |
| 10967 | 22 | 28.7 | 1 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 |
| ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... |
| 1135 | 51 | 29.8 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 1 | 0 |
| 1706 | 50 | 26.6 | 1 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 |
| 11205 | 24 | 23.7 | 1 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 1 | 0 |
| 12323 | 36 | 35.9 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 1 |
| 15604 | 29 | -9.0 | 1 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 1 | 0 |
5000行 × 16列
我们定义了一个灵活的模型,该模型使用BART模型估计结果,并使用更简单的线性回归估计中介变量。然而,我们将两者嵌入一个线性方程中,以捕捉所需的系数,从而“读取”吸烟对健康支出的总效应、间接效应和直接效应,这些效应是通过健康来中介的。
def mediation_model(X_m, t, m, y):
with pm.Model(coords={"coeffs": list(X_m.columns), "obs_id": range(len(X_m))}) as model:
t_data = pm.MutableData("t", t, dims="obs_id")
m = pm.MutableData("m", m, dims="obs_id")
X_data = pm.MutableData("X", X_m)
# intercept priors
im = pm.Normal("im", mu=0, sigma=10)
iy = pm.Normal("iy", mu=0, sigma=10)
# slope priors
a = pm.Normal("a", mu=0, sigma=1)
b = pm.Normal("b", mu=0, sigma=1)
cprime = pm.Normal("cprime", mu=0, sigma=1)
# noise priors
sigma1 = pm.Exponential("sigma1", 1)
sigma2 = pm.Exponential("sigma2", 1)
bart_mu = pmb.BART("mu", X_data, y)
beta = pm.Normal("beta", mu=0, sigma=1, dims="coeffs")
mu_m = pm.Deterministic("mu_m", pm.math.dot(X_data, beta), dims="obs_id")
# likelihood
pm.Normal(
"mlikelihood", mu=(im + a * t_data) + mu_m, sigma=sigma1, observed=m, dims="obs_id"
)
pm.Normal(
"ylikelihood",
mu=iy + b * m + cprime * t_data + bart_mu,
sigma=sigma2,
observed=y,
dims="obs_id",
)
# calculate quantities of interest
indirect_effect = pm.Deterministic("indirect effect", a * b)
total_effect = pm.Deterministic("total effect", a * b + cprime)
return model
model = mediation_model(X_m, t, m, y)
pm.model_to_graphviz(model)
with model:
result = pm.sample(tune=1000, random_seed=42, target_accept=0.95)
Multiprocess sampling (4 chains in 4 jobs)
CompoundStep
>NUTS: [im, iy, a, b, cprime, sigma1, sigma2, beta]
>PGBART: [mu]
Sampling 4 chains for 1_000 tune and 1_000 draw iterations (4_000 + 4_000 draws total) took 164 seconds.
The rhat statistic is larger than 1.01 for some parameters. This indicates problems during sampling. See https://arxiv.org/abs/1903.08008 for details
The effective sample size per chain is smaller than 100 for some parameters. A higher number is needed for reliable rhat and ess computation. See https://arxiv.org/abs/1903.08008 for details
ax = az.plot_posterior(
result,
var_names=["cprime", "indirect effect", "total effect"],
ref_val=0,
hdi_prob=0.95,
figsize=(20, 6),
)
ax[0].set(title="direct effect");
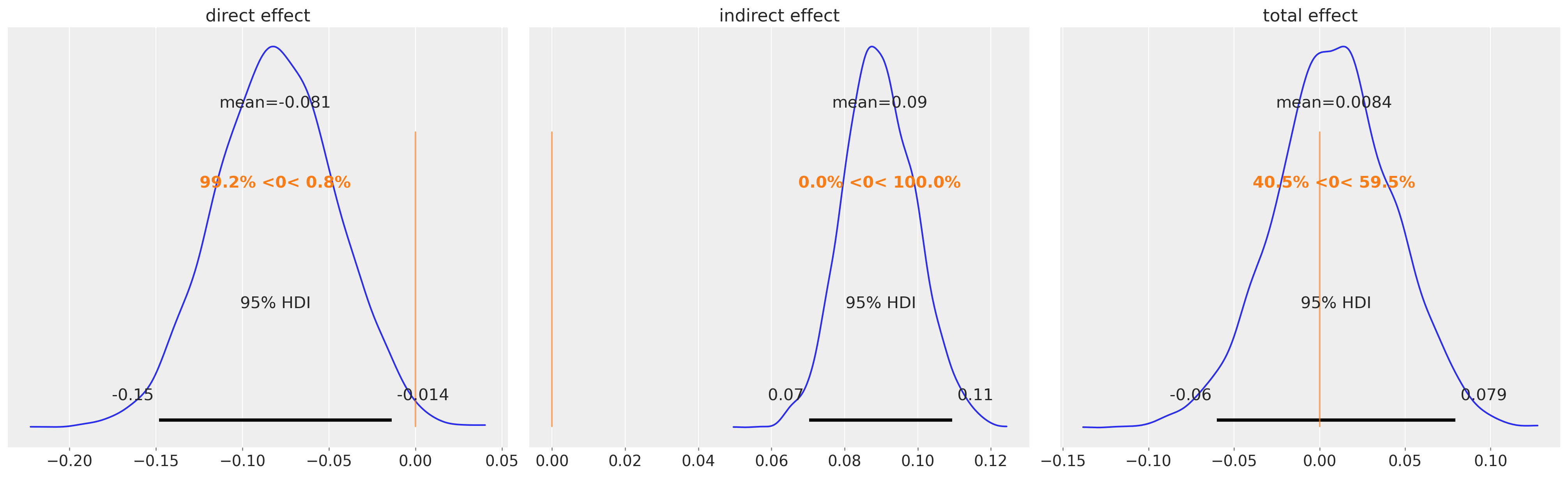
在这里,我们开始了解发生了什么。吸烟的影响是直接负面的,但通过健康状况这一中介的间接效应是正面的,并且综合效应抵消/减少了治疗对结果的影响。使用这种新结构,我们当然可以使用回归插补法进行因果推断,并推导出一种关于吸烟通过观察到的健康特征产生影响的“其他条件不变”定律。更简洁地,我们可以使用潜在结果框架推导出因果中介估计量,这种方法不依赖于结果和中介模型的函数形式。
中介估计量#
在中介分析中,我们致力于认为问题的正确因果结构是由处理变量和感兴趣的结果之间的中断影响路径表示的。这意味着处理有预期的效果,但我们需要做更多的工作来解开处理对结果的自然直接效应(NDE)和自然间接效应(NIE)。
这些量使用潜在结果表示法表示如下:
设 \(M(t)\) 为在治疗规范 \(t\) 下中介变量的值。
然后 \(Y(t, M(t))\) 是我们结果变量 Y 的一个“嵌套”潜在结果,依赖于基于 \(t\) 的 \(M\) 的实现。
将\(t\) 区分作为处理变量的特定设置在 \(\{ 0, 1\}\) 中,与 \(t^{*}\) 作为替代设置。
现在我们定义
NDE: \(E[Y(t, M(t^{*})) - Y(t^{*}, M(t^{*}))]\)
也就是说,我们对在特定治疗方案下,通过M值介导的不同治疗结果之间的差异感兴趣。
NIE: \(E[(Y(t, M(t))) - Y(t, M(t^{*}))]\)
这相当于由于生成中介值 M 的治疗方案的差异导致的结局 Y 的差异。
总效应: 直接效应 + 间接效应
这些方程式很微妙,潜在结果的表示法可能有点晦涩,但这是我们继承的表示法。关键点是,在NDE中,中介效应的处理机制是固定的,而结果的值是变化的。在NIE中,中介效应的值是变化的,而结果变量的处理机制是固定的。
我们将演示如何使用反事实插补方法来恢复因果中介估计量,并将这些插补的中介值适当地代入NDE和NIE的公式中。我们基于上述拟合初始中介模型时得到的结果数据对象result进行这些计算。
def counterfactual_mediation(model, result, X, treatment_status=1):
if treatment_status == 1:
t_mod = np.ones(len(X), dtype="int32")
else:
t_mod = np.zeros(len(X), dtype="int32")
with model:
# update values of predictors:
pm.set_data({"t": t_mod})
idata = pm.sample_posterior_predictive(result, var_names=["mlikelihood"], progressbar=False)
return idata
### Impute Mediation values under different treatment regimes
### To be used to vary the imputation efforts of the outcome variable in the
### NDE and NIE calculations below.
idata_1m = counterfactual_mediation(model, result, X_m, treatment_status=1)
idata_0m = counterfactual_mediation(model, result, X_m, treatment_status=0)
def counterfactual_outcome(
model, result, m_idata, sample_index=0, treatment_status=1, modified_m=True
):
"""Ensure we can change sample_index so we can post-process the mediator posterior predictive
distributions and derive posterior predictive views of the conditional variation in the outcome.
"""
if treatment_status == 1:
t_mod = np.ones(len(X), dtype="int32")
m_mod = az.extract(m_idata["posterior_predictive"]["mlikelihood"])["mlikelihood"][
:, sample_index
].values.astype(int)
else:
t_mod = np.zeros(len(X), dtype="int32")
m_mod = az.extract(m_idata["posterior_predictive"]["mlikelihood"])["mlikelihood"][
:, sample_index
].values.astype(int)
if not modified_m:
m_mod = result["constant_data"]["m"].values
with model:
# update values of predictors:
pm.set_data({"t": t_mod, "m": m_mod})
idata = pm.sample_posterior_predictive(result, var_names=["ylikelihood"], progressbar=False)
return idata
### Using one draw from the posterior of the mediation inference objects.
### We vary the treatment of the outcome but keep the Mediator values static under
### the counterfactual regime of no treatment
idata_nde1 = counterfactual_outcome(model, result, m_idata=idata_0m, treatment_status=1)
idata_nde0 = counterfactual_outcome(model, result, m_idata=idata_0m, treatment_status=0)
### We fix the treatment regime for the outcome but vary the mediator status
### between those counterfactual predictions and the observed mediator values
idata_nie0 = counterfactual_outcome(model, result, m_idata=idata_0m, treatment_status=0)
idata_nie1 = counterfactual_outcome(
model, result, m_idata=idata_0m, treatment_status=0, modified_m=False
)
Sampling: [mlikelihood]
Sampling: [mlikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
### Natural Direct Effect
nde = (
idata_nde1["posterior_predictive"]["ylikelihood"].mean()
- idata_nde0["posterior_predictive"]["ylikelihood"].mean()
)
nde
<xarray.DataArray 'ylikelihood' ()> array(-0.08185824)
### Natural InDirect Effect
nie = (
idata_nie0["posterior_predictive"]["ylikelihood"].mean()
- idata_nie1["posterior_predictive"]["ylikelihood"].mean()
)
nie
<xarray.DataArray 'ylikelihood' ()> array(0.08437854)
### Total Effect
nde + nie
<xarray.DataArray 'ylikelihood' ()> array(0.0025203)
注意我们如何以这种方式恢复估计值,这些估计值反映了从上述中介模型推导出的典型公式。然而,重要的是,无论我们的中介和结果模型的参数构造如何,这种插补方法都是可行的。
接下来,我们通过从中介值的反事实后验中抽取样本,来推导因果估计量的后验预测分布。
estimands = []
for i in range(400):
idata_nde1 = counterfactual_outcome(
model, result, m_idata=idata_0m, treatment_status=1, sample_index=i
)
idata_nde0 = counterfactual_outcome(
model, result, m_idata=idata_0m, treatment_status=0, sample_index=i
)
idata_nie0 = counterfactual_outcome(
model, result, m_idata=idata_0m, treatment_status=0, sample_index=i
)
idata_nie1 = counterfactual_outcome(
model, result, m_idata=idata_0m, treatment_status=0, modified_m=False, sample_index=i
)
nde = (
idata_nde1["posterior_predictive"]["ylikelihood"].mean()
- idata_nde0["posterior_predictive"]["ylikelihood"].mean()
)
nie = (
idata_nie0["posterior_predictive"]["ylikelihood"].mean()
- idata_nie1["posterior_predictive"]["ylikelihood"].mean()
)
te = nde + nie
estimands.append([nde.item(), nie.item(), te.item()])
estimands_df = pd.DataFrame(
estimands, columns=["Natural Direct Effect", "Natural Indirect Effect", "Total Effect"]
)
Show code cell output
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
Sampling: [ylikelihood]
estimands_df.head()
| Natural Direct Effect | Natural Indirect Effect | Total Effect | |
|---|---|---|---|
| 0 | -0.081381 | 0.084770 | 0.003389 |
| 1 | -0.081198 | 0.091234 | 0.010036 |
| 2 | -0.081428 | 0.100242 | 0.018814 |
| 3 | -0.081012 | 0.079501 | -0.001511 |
| 4 | -0.080959 | 0.096993 | 0.016034 |
Show code cell source
fig, axs = plt.subplots(1, 3, figsize=(25, 8))
axs = axs.flatten()
axs[0].hist(estimands_df["Natural Direct Effect"], bins=20, ec="black", color="red", alpha=0.3)
axs[1].hist(estimands_df["Natural Indirect Effect"], bins=20, ec="black", alpha=0.3)
axs[2].hist(estimands_df["Total Effect"], bins=20, ec="black", color="slateblue")
axs[2].axvline(
estimands_df["Total Effect"].mean(),
color="black",
linestyle="--",
label="Expected Total Effect",
)
axs[1].axvline(
estimands_df["Natural Indirect Effect"].mean(),
color="black",
linestyle="--",
label="Expected NIE",
)
axs[0].axvline(
estimands_df["Natural Direct Effect"].mean(),
color="black",
linestyle="--",
label="Expected NDE",
)
axs[0].set_title("Posterior Predictive Distribution \n Natural Direct Effect")
axs[0].set_xlabel("Change in Log(Expenditure)")
axs[1].set_xlabel("Change in Log(Expenditure)")
axs[2].set_xlabel("Change in Log(Expenditure)")
axs[1].set_title("Posterior Predictive Distribution \n Natural Indirect Effect")
axs[2].set_title("Posterior Predictive Distribution \n Total Effect")
axs[2].legend()
axs[1].legend()
axs[0].legend()
plt.suptitle(
"Causal Mediation Estimands \n Using Potential Outcomes", fontsize=20, fontweight="bold"
);
结论#
倾向评分是思考因果推断问题结构的有用工具。它们直接关系到选择效应的考虑,并可以主动用于重新加权从观察数据集中获得的证据。它们可以与灵活的机器学习模型和交叉验证技术一起应用,以纠正像BART这样的机器学习模型的过拟合。它们不像贝叶斯先验那样是模型拟合正则化的直接工具,但它们是同一类工具。它们要求分析师提供治疗分配机制的理论——在强可忽略性下,这足以评估感兴趣结果的政策变化。
在双重稳健估计方法和因果推断的去偏机器学习方法中,倾向评分的作用强调了结果变量理论与处理分配机制理论之间的平衡。我们已经看到,盲目地将机器学习模型应用于因果问题可能导致处理分配模型的不当设定,并基于天真的点估计得出严重偏斜的估计结果。Angrist 和 Pischke 认为,这应该促使我们回归到谨慎和细致的回归建模的安全性。即使在去偏机器学习模型的案例中,也隐含地呼吁回归估计量来支持 Frisch-Waugh-Lowell 结果。但在这里,匆忙的方法也会导致反直觉的主张。这些思维工具中的每一个都有其应用范围——理解其局限性对于支持可信的因果主张至关重要。
我们已经看到的大量结果突显了需要对数据生成模型的结构给予仔细关注。最后一个例子强调了因果推断与因果结构图推断之间的紧密联系。通过因果结构传播的不确定性确实非常重要!希望这些结构能通过机器学习的魔力自动识别,这只不过是异想天开。我们已经看到倾向评分方法如何寻求通过重新加权推断作为纠正步骤,我们已经看到双重稳健方法如何通过机器学习策略的预测能力来纠正推断,最后我们还看到了结构建模如何通过在协变量之间路径的影响上施加约束来纠正估计。
这就是推理的进行方式。你编码你对世界的知识,并随着证据的积累更新你的观点。因果推理需要对世界的结构观点的承诺,我们不能在推理变得站不住脚时假装无知。
参考资料#
MA Hernán 和 JM Robins。《因果推断:何为因果》。Chapman & Hall/CRC,2020。
Chernozhukov Victor, Chetverikov Denis, Demirer Mert, Duflo Esther, Hansen Christian, Newey Whitney, 和 Robins James. 双重/去偏机器学习用于处理和结构参数。计量经济学杂志,21(1):1 – 68, 2018. doi:https://doi.org/10.1111/ectj.12097.
水印#
%load_ext watermark
%watermark -n -u -v -iv -w -p pytensor
Last updated: Sat Feb 24 2024
Python implementation: CPython
Python version : 3.9.16
IPython version : 8.12.0
pytensor: 2.11.1
pandas : 1.5.3
numpy : 1.24.4
networkx : 3.2.1
arviz : 0.17.0
pymc : 5.3.0
pymc_bart : 0.5.7
xarray : 2024.1.1
pytensor : 2.11.1
matplotlib : 3.8.2
statsmodels: 0.13.5
Watermark: 2.3.1