带有截断或删失数据的贝叶斯回归#
该笔记本提供了一个示例,展示了当您的结果变量被截断或截断时如何进行线性回归。
from copy import copy
import arviz as az
import matplotlib.pyplot as plt
import numpy as np
import pymc as pm
import xarray as xr
from numpy.random import default_rng
from scipy.stats import norm, truncnorm
%config InlineBackend.figure_format = 'retina'
rng = default_rng(12345)
az.style.use("arviz-darkgrid")
截断与删失#
截断和删失是缺失数据问题的例子。有时很容易混淆截断和删失,所以让我们来看一些定义。
截断是一种缺失数据问题,其中您对结果变量超出某个边界范围的任何数据完全不知情。
审查发生在测量具有一定界限的敏感性时。但与其丢弃超出这些界限的数据,不如记录超出界限的测量值。
让我们通过一些代码和图表进一步探讨这一点。首先,我们将生成一些真实的 (x, y) 散点数据,其中 y 是我们的结果度量,而 x 是一些预测变量。
slope, intercept, σ, N = 1, 0, 2, 200
x = rng.uniform(-10, 10, N)
y = rng.normal(loc=slope * x + intercept, scale=σ)
对于这个(x, y)散点数据的示例,我们可以将截断过程描述为简单地过滤掉任何结果变量y超出设定边界的数据。
def truncate_y(x, y, bounds):
keep = (y >= bounds[0]) & (y <= bounds[1])
return (x[keep], y[keep])
然而,在审查的情况下,我们将 y 值设置为它们超过的界限。
def censor_y(x, y, bounds):
cy = copy(y)
cy[y <= bounds[0]] = bounds[0]
cy[y >= bounds[1]] = bounds[1]
return (x, cy)
基于我们生成的(x, y)数据(这是实验者在现实生活中永远看不到的),我们可以生成我们实际观察到的截断数据(xt, yt)和删失数据(xc, yc)的数据集。
bounds = [-5, 5]
xt, yt = truncate_y(x, y, bounds)
xc, yc = censor_y(x, y, bounds)
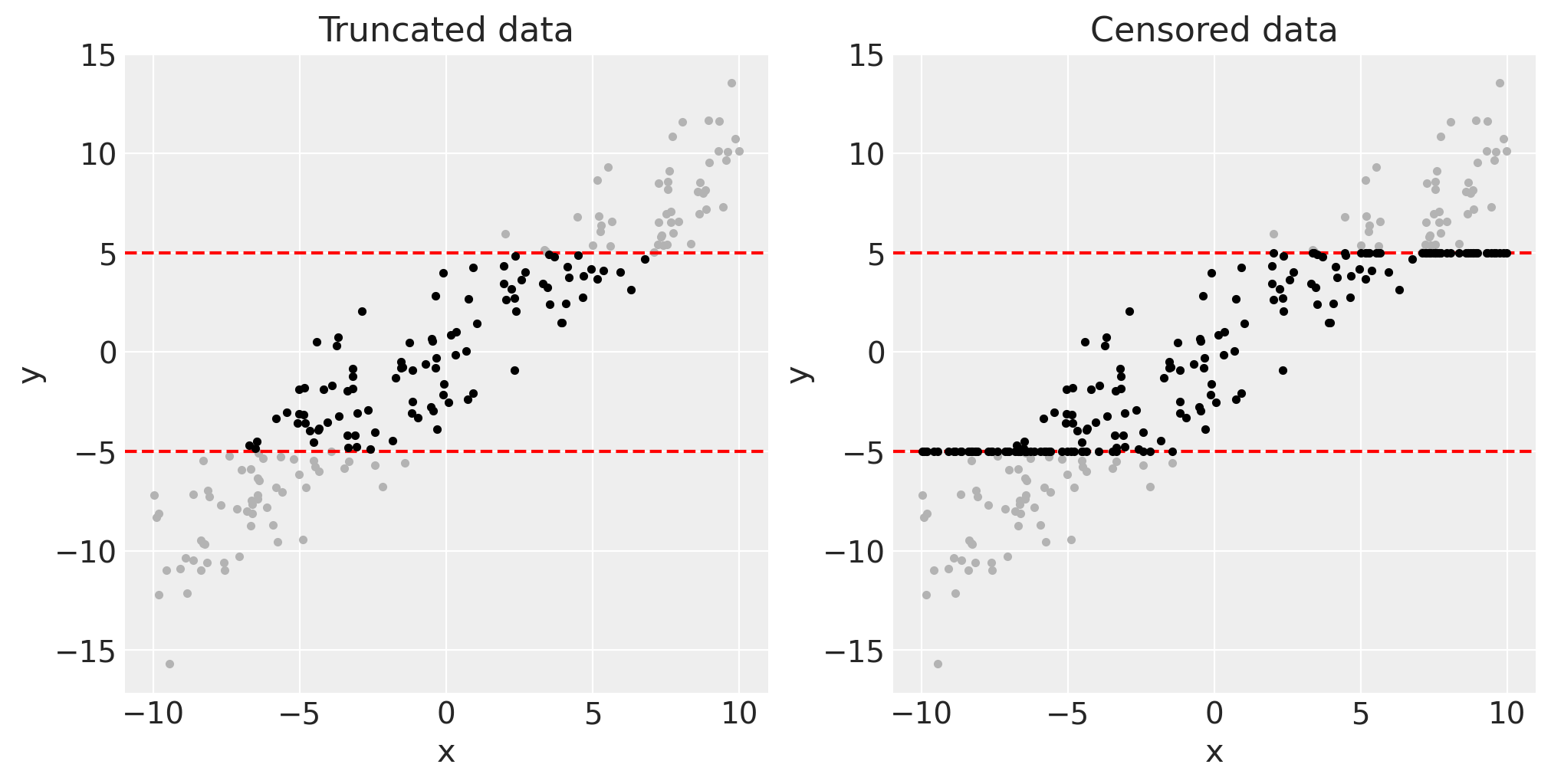
我们可以将这些潜在数据(灰色)和剩余的截断或删失数据(黑色)可视化如下。
fig, axes = plt.subplots(1, 2, figsize=(10, 5))
for ax in axes:
ax.plot(x, y, ".", c=[0.7, 0.7, 0.7])
ax.axhline(bounds[0], c="r", ls="--")
ax.axhline(bounds[1], c="r", ls="--")
ax.set(xlabel="x", ylabel="y")
axes[0].plot(xt, yt, ".", c=[0, 0, 0])
axes[0].set(title="Truncated data")
axes[1].plot(xc, yc, ".", c=[0, 0, 0])
axes[1].set(title="Censored data");
截断或删失回归解决的问题#
如果我们对截断数据或删失数据运行常规线性回归,应该很容易理解我们可能会低估斜率。截断回归和删失回归(也称为Tobit回归)旨在解决这些缺失数据问题,并希望得到不受截断或删失引入偏差影响的回归斜率。
在本节中,我们将在这些数据集上运行贝叶斯线性回归,以了解问题的程度。我们首先定义一个函数,该函数定义一个PyMC模型,进行MCMC采样,并返回模型和MCMC采样数据。
因此,我们可以分别在截断数据和删失数据上运行此操作。
trunc_linear_model = linear_regression(xt, yt)
with trunc_linear_model:
trunc_linear_fit = pm.sample()
Sampling 4 chains for 1_000 tune and 1_000 draw iterations (4_000 + 4_000 draws total) took 1 seconds.
cens_linear_model = linear_regression(xc, yc)
with cens_linear_model:
cens_linear_fit = pm.sample()
Sampling 4 chains for 1_000 tune and 1_000 draw iterations (4_000 + 4_000 draws total) took 1 seconds.
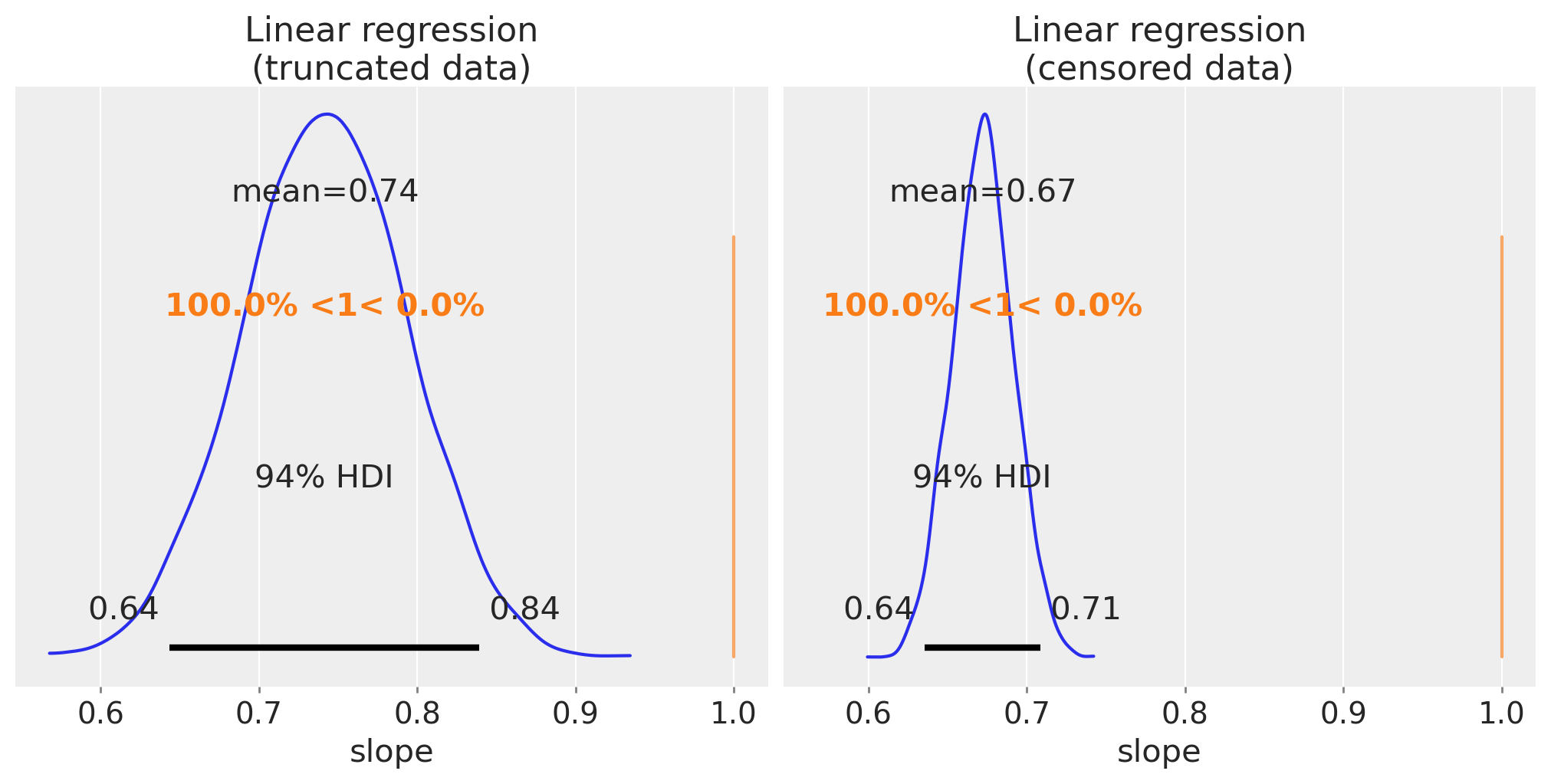
通过绘制斜率参数的后验分布,我们可以看到斜率的估计值相差很大,因此我们确实低估了回归斜率。
fig, ax = plt.subplots(1, 2, figsize=(10, 5), sharex=True)
az.plot_posterior(trunc_linear_fit, var_names=["slope"], ref_val=slope, ax=ax[0])
ax[0].set(title="Linear regression\n(truncated data)", xlabel="slope")
az.plot_posterior(cens_linear_fit, var_names=["slope"], ref_val=slope, ax=ax[1])
ax[1].set(title="Linear regression\n(censored data)", xlabel="slope");
为了理解问题的严重性(对于这个数据集),我们可以将后验预测拟合与数据一起可视化。
def pp_plot(x, y, fit, ax):
# plot data
ax.plot(x, y, "k.")
# plot posterior predicted... samples from posterior
xi = xr.DataArray(np.array([np.min(x), np.max(x)]), dims=["obs_id"])
post = az.extract(fit)
y_ppc = xi * post["slope"] + post["intercept"]
ax.plot(xi, y_ppc, c="steelblue", alpha=0.01, rasterized=True)
# plot true
ax.plot(xi, slope * xi + intercept, "k", lw=3, label="True")
# plot bounds
ax.axhline(bounds[0], c="r", ls="--")
ax.axhline(bounds[1], c="r", ls="--")
ax.legend()
ax.set(xlabel="x", ylabel="y")
fig, ax = plt.subplots(1, 2, figsize=(10, 5), sharex=True, sharey=True)
pp_plot(xt, yt, trunc_linear_fit, ax[0])
ax[0].set(title="Truncated data")
pp_plot(xc, yc, cens_linear_fit, ax[1])
ax[1].set(title="Censored data");
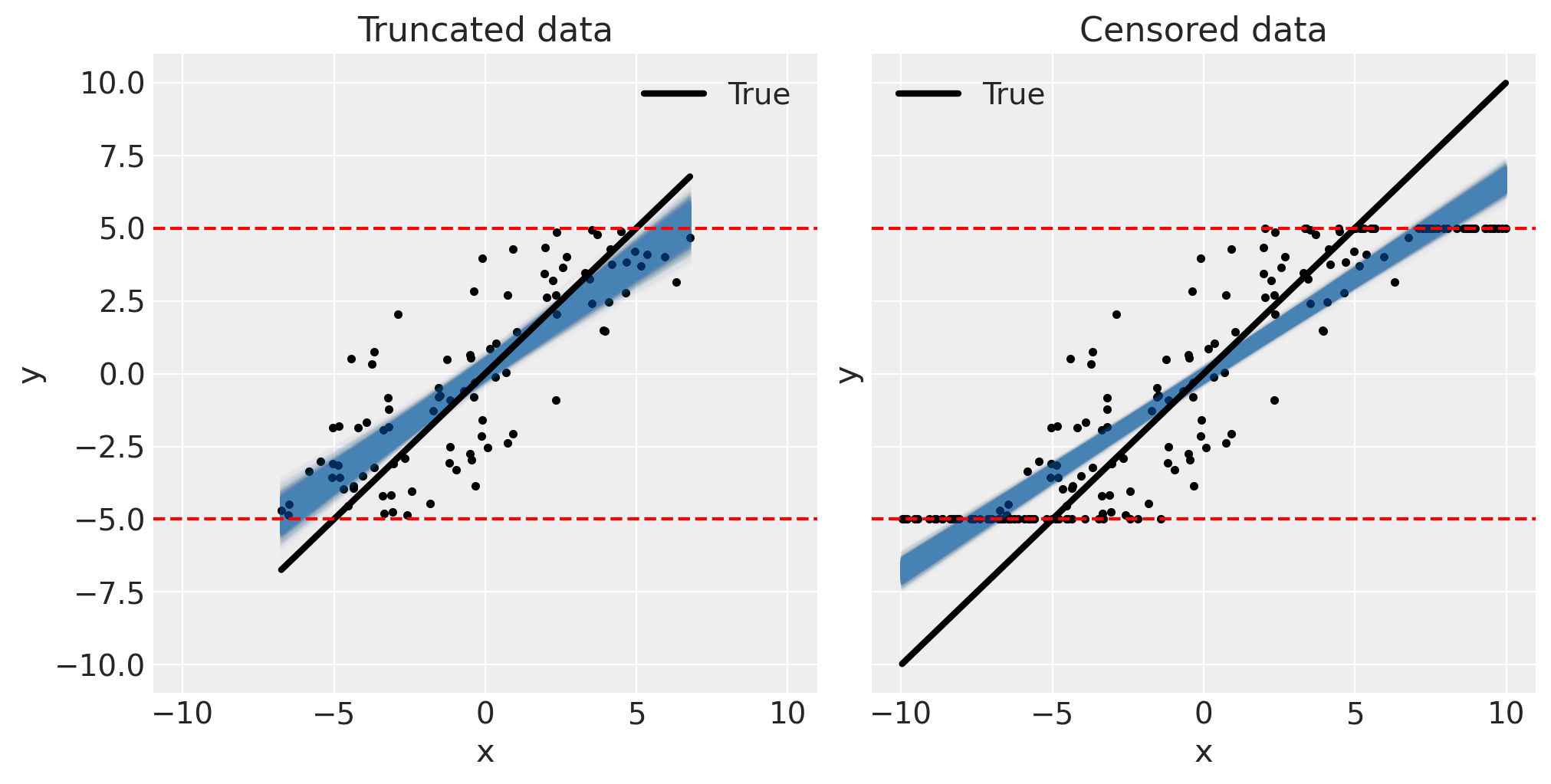
通过观察这些图表,我们可以直观地预测哪些因素会影响低估偏差的程度。首先,如果截断或删失边界非常宽泛,以至于它们只影响少数数据点,那么低估偏差将会较小。其次,如果测量误差σ较低,我们可能会预期低估偏差会减少。在测量噪声为零的极限情况下,应该可以完全恢复截断数据的真正斜率,但在删失情况下总是会存在一些偏差。无论如何,除非测量误差接近零,或者边界宽泛到实际上无关紧要,否则使用截断或删失回归模型将是明智的选择。
实现截断和删失回归模型#
现在我们已经看到了在截断或删失数据上进行回归的问题,即低估回归斜率。这就是截断或删失回归模型被设计来解决的问题。截断回归和删失回归的总体方法是将我们对数据生成过程中截断或删失步骤的先验知识编码进去。这是通过以各种方式修改似然函数来实现的。
截断回归模型#
截断回归模型实现起来非常简单。正态似然像往常一样以回归斜率为中心,但现在我们只需指定一个在边界处截断的正态分布。
def truncated_regression(x, y, bounds):
with pm.Model() as model:
slope = pm.Normal("slope", mu=0, sigma=1)
intercept = pm.Normal("intercept", mu=0, sigma=1)
σ = pm.HalfNormal("σ", sigma=1)
normal_dist = pm.Normal.dist(mu=slope * x + intercept, sigma=σ)
pm.Truncated("obs", normal_dist, lower=bounds[0], upper=bounds[1], observed=y)
return model
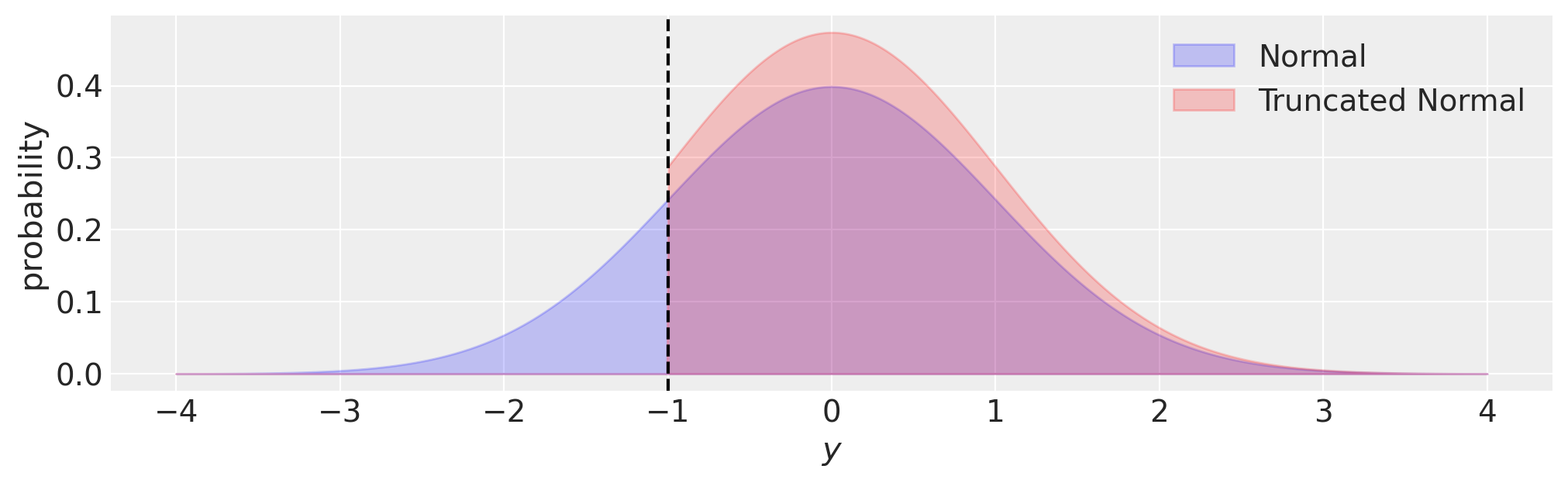
截断回归通过更新似然函数来反映我们对生成观测值过程的了解,从而解决了偏差问题。也就是说,我们没有机会观察到截断边界之外的任何数据,因此似然函数应该反映这一点。我们可以在下面的图中可视化这一点,与正态分布相比,在这种情况下,截断正态分布的概率密度在截断边界 \((y<-1)\) 之外为零。
fig, ax = plt.subplots(figsize=(10, 3))
y = np.linspace(-4, 4, 1000)
ax.fill_between(y, norm.pdf(y, loc=0, scale=1), 0, alpha=0.2, ec="b", fc="b", label="Normal")
ax.fill_between(
y,
truncnorm.pdf(y, -1, float("inf"), loc=0, scale=1),
0,
alpha=0.2,
ec="r",
fc="r",
label="Truncated Normal",
)
ax.set(xlabel="$y$", ylabel="probability")
ax.axvline(-1, c="k", ls="--")
ax.legend();
审查回归模型#
def censored_regression(x, y, bounds):
with pm.Model() as model:
slope = pm.Normal("slope", mu=0, sigma=1)
intercept = pm.Normal("intercept", mu=0, sigma=1)
σ = pm.HalfNormal("σ", sigma=1)
y_latent = pm.Normal.dist(mu=slope * x + intercept, sigma=σ)
obs = pm.Censored("obs", y_latent, lower=bounds[0], upper=bounds[1], observed=y)
return model
得益于新的 pm.Censored 分布,编写带有截断数据的模型变得非常简单。唯一需要记住的是,被截断的潜在变量必须使用 .dist 方法来调用,如上例中的 pm.Normal.dist。
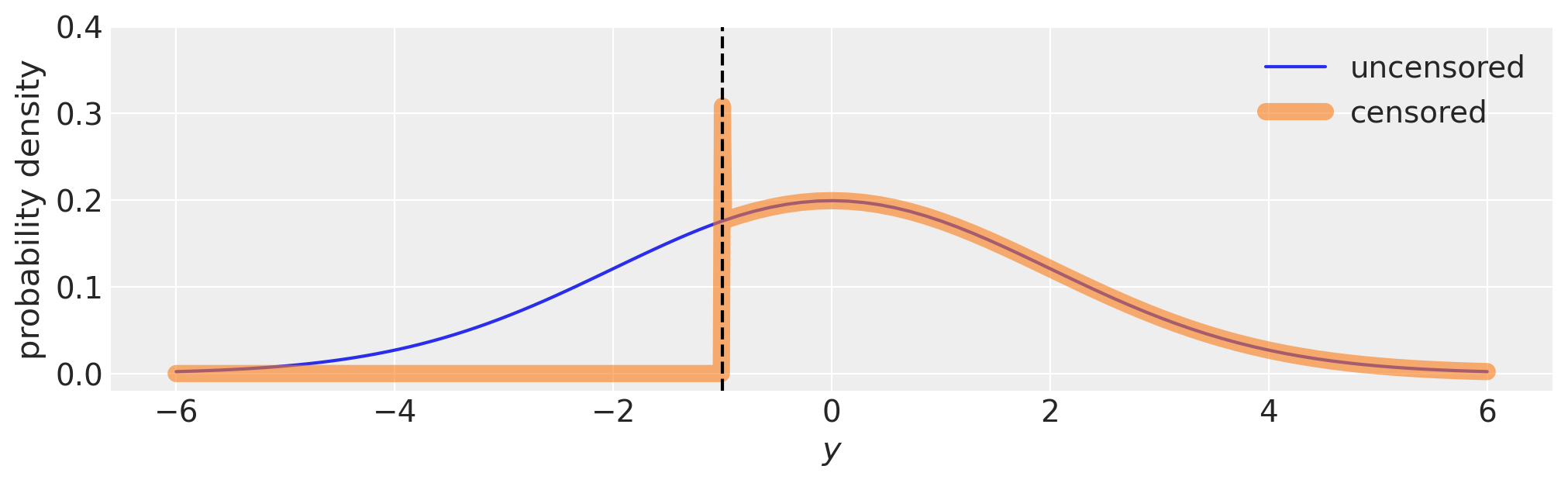
在幕后,pm.Censored 调整了似然函数,以考虑到以下情况:
下限处的概率等于从\(-\infty\)到下限的累积分布函数。
上界处的概率等于从上界到\(\infty\)的累积分布函数。
这在下面的图中可以直观地展示出来。从技术上讲,边界处的概率密度是无限的,因为边界处的箱宽正好为零。
fig, ax = plt.subplots(figsize=(10, 3))
with pm.Model() as m:
pm.Normal("y", 0, 2)
with pm.Model() as m_censored:
pm.Censored("y", pm.Normal.dist(0, 2), lower=-1.0, upper=None)
logp_fn = m.compile_logp()
logp_censored_fn = m_censored.compile_logp()
xi = np.hstack((np.linspace(-6, -1.01), [-1.0], np.linspace(-0.99, 6)))
ax.plot(xi, [np.exp(logp_fn({"y": x})) for x in xi], label="uncensored")
ax.plot(xi, [np.exp(logp_censored_fn({"y": x})) for x in xi], label="censored", lw=8, alpha=0.6)
ax.axvline(-1, c="k", ls="--")
ax.legend()
ax.set(xlabel="$y$", ylabel="probability density", ylim=(-0.02, 0.4));
运行截断和删失回归#
现在我们可以在截断数据上使用截断回归模型进行参数估计…
truncated_model = truncated_regression(xt, yt, bounds)
with truncated_model:
truncated_fit = pm.sample()
Sampling 4 chains for 1_000 tune and 1_000 draw iterations (4_000 + 4_000 draws total) took 1 seconds.
并在删失数据上使用删失回归模型。
censored_model = censored_regression(xc, yc, bounds)
with censored_model:
censored_fit = pm.sample(init="adapt_diag")
Sampling 4 chains for 1_000 tune and 1_000 draw iterations (4_000 + 4_000 draws total) took 1 seconds.
我们可以像之前一样,将我们对斜率的后验估计进行可视化。
fig, ax = plt.subplots(1, 2, figsize=(10, 5), sharex=True)
az.plot_posterior(truncated_fit, var_names=["slope"], ref_val=slope, ax=ax[0])
ax[0].set(title="Truncated regression\n(truncated data)", xlabel="slope")
az.plot_posterior(censored_fit, var_names=["slope"], ref_val=slope, ax=ax[1])
ax[1].set(title="Censored regression\n(censored data)", xlabel="slope");
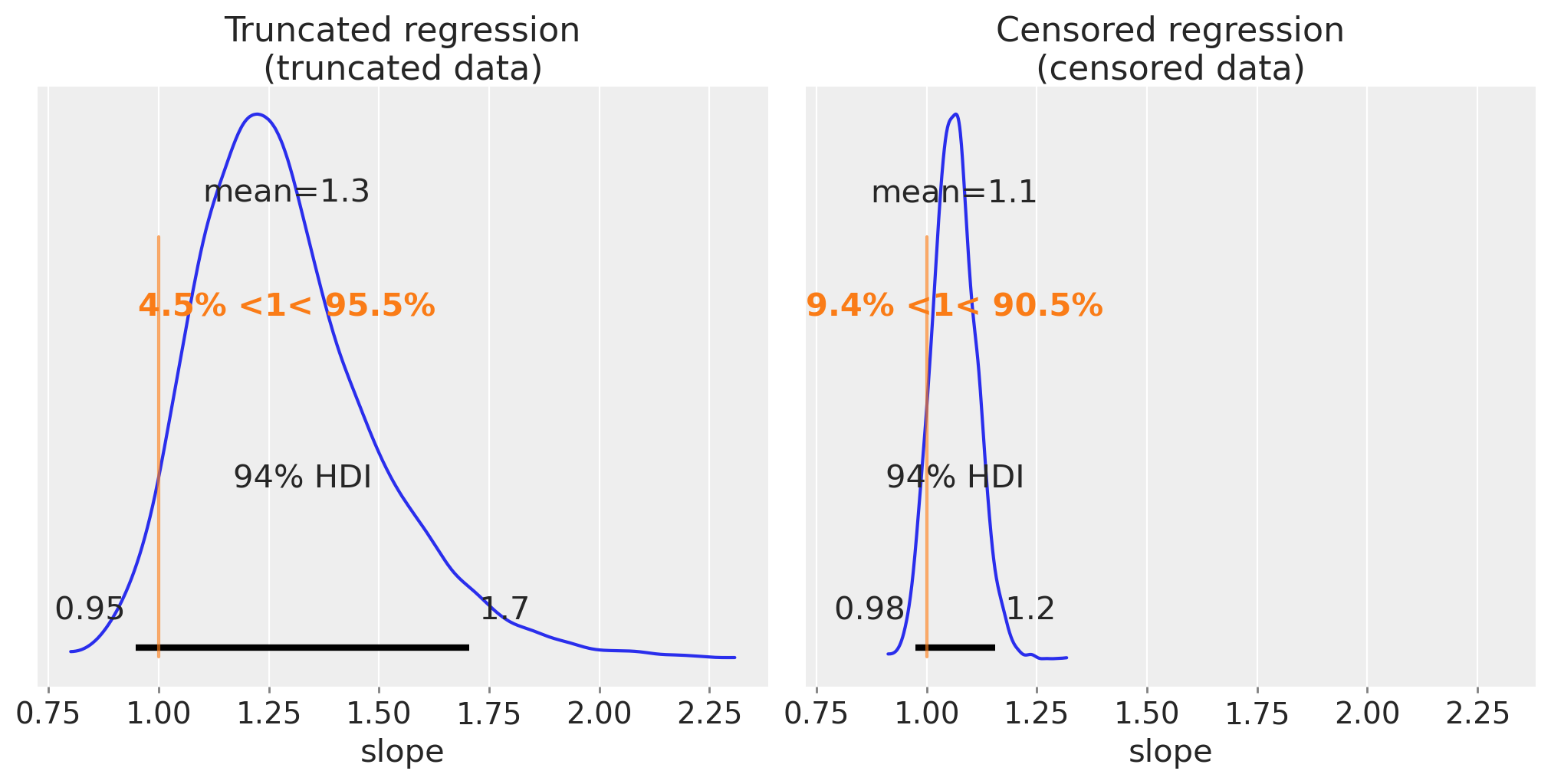
这些是更好的估计。有趣的是,我们可以看到删失回归的估计比截断数据的估计更精确。这并不一定总是如此,但这里的直觉是,截断时x和y数据完全被丢弃,而在删失中只有y数据变得部分未知。
我们可以推测,如果实验者可以选择截断或删失数据,那么选择删失可能比截断更好。
相应地,我们可以通过视觉检查后验预测图来确认模型是好的。
fig, ax = plt.subplots(1, 2, figsize=(10, 5), sharex=True, sharey=True)
pp_plot(xt, yt, truncated_fit, ax[0])
ax[0].set(title="Truncated data")
pp_plot(xc, yc, censored_fit, ax[1])
ax[1].set(title="Censored data");
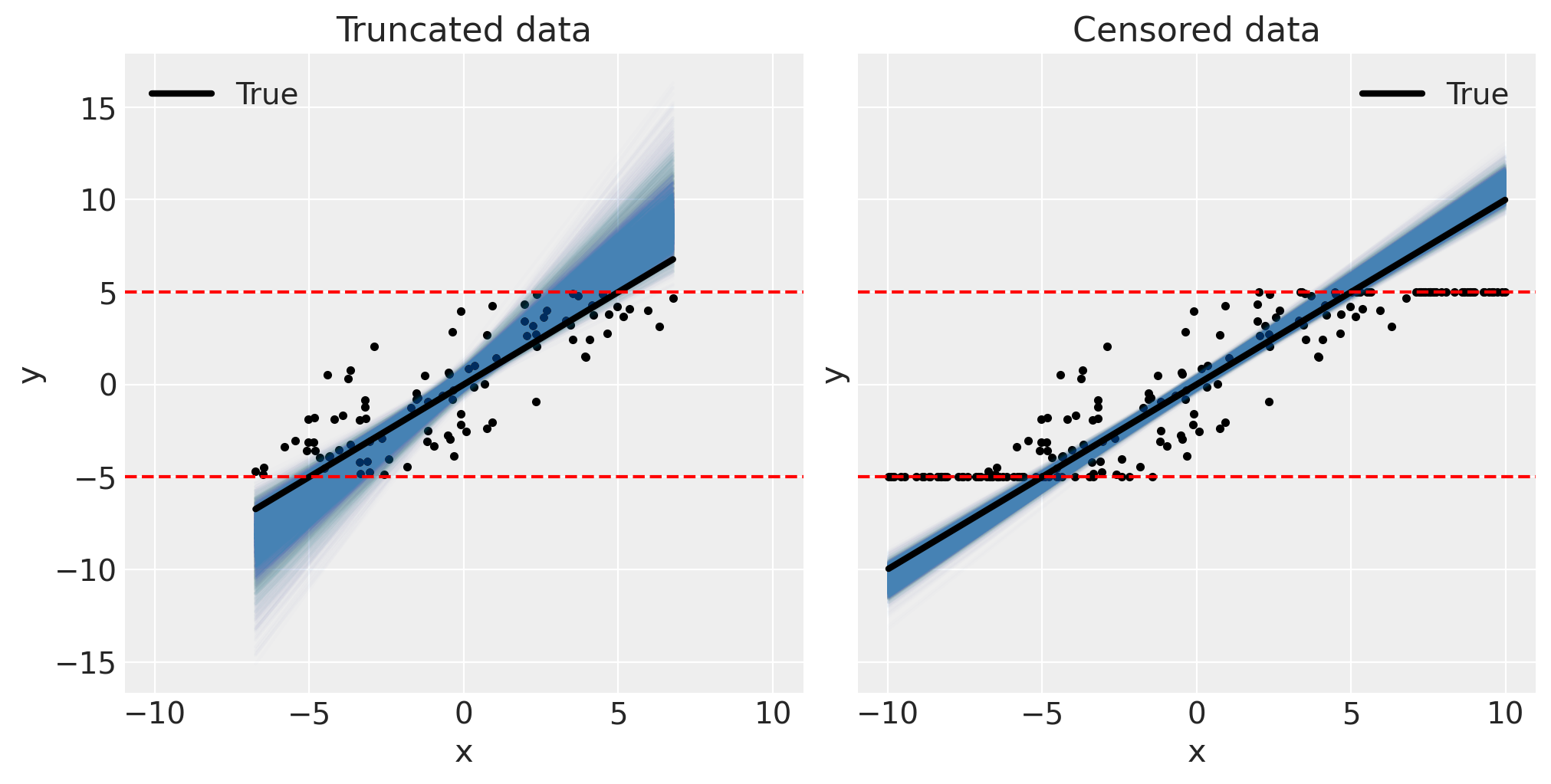
这标志着我们在PyMC中关于截断数据和审查数据以及截断和审查回归模型的指南的结束。虽然回归斜率估计偏差的程度会因上述讨论的多个因素而有所不同,但希望这些示例已经使您相信将您对数据生成过程的知识编码到回归分析中的重要性。
进一步的主题#
也可以将边界视为未知的潜在参数。如果这些边界不完全已知,并且可以对这些边界进行先验假设,那么就可以推断出这些边界是什么。然而,这可能被认为是过度设计——根据您的数据分析背景,提取“足够好”的边界点估计值以获得合理的回归估计可能已经完全足够。
上述的审查回归模型采用了一种特定的方法,还有其他方法。例如,它没有尝试推断审查数据的真实潜在y值的后验信念。可以构建审查回归模型来推断这些审查的y值,但我们在这里没有讨论这个问题,因为插补这个主题值得单独深入探讨。PyMC的审查数据模型示例也涵盖了这个主题,特别是一个用于推断审查数据的示例模型。
进一步阅读#
在研究这个主题时,我发现大多数资料都集中在最大似然估计方法上,重点是数学推导而不是实际实现。Breen 等人 [1996] 的一本简洁的数学小册子(80页)涵盖了截断和删失以及其他缺失数据场景。尽管如此,Gelman et al. [2013] 的《贝叶斯数据分析》中有几页涉及这个主题,以及 Gelman et al. [2020]。
参考资料#
水印#
%load_ext watermark
%watermark -n -u -v -iv -w -p pytensor,aeppl
Last updated: Sun Feb 05 2023
Python implementation: CPython
Python version : 3.10.9
IPython version : 8.9.0
pytensor: 2.8.11
aeppl : not installed
numpy : 1.24.1
arviz : 0.14.0
matplotlib: 3.6.3
pymc : 5.0.1
xarray : 2023.1.0
Watermark: 2.3.1