通用 API 快速入门

import arviz as az
import matplotlib.pyplot as plt
import numpy as np
import pymc as pm
import pytensor.tensor as pt

/home/xian/anaconda3/envs/pymc-dev-py39/lib/python3.9/site-packages/pkg_resources/__init__.py:123: PkgResourcesDeprecationWarning: main is an invalid version and will not be supported in a future release
  warnings.warn(

RANDOM_SEED = 8927
rng = np.random.default_rng(RANDOM_SEED)
az.style.use("arviz-darkgrid")

1. 模型创建

PyMC 中的模型围绕 Model 类展开。它包含所有随机变量 (RVs) 的引用，并计算模型的对数概率及其梯度。通常，您会将其作为 with 上下文的一部分进行实例化：

with pm.Model() as model:
    # Model definition
    pass

我们在下面进一步讨论RVs，但让我们创建一个简单的模型来探索Model类。

with pm.Model() as model:
    mu = pm.Normal("mu", mu=0, sigma=1)
    obs = pm.Normal("obs", mu=mu, sigma=1, observed=rng.standard_normal(100))

model.basic_RVs

[mu ~ N(0, 1), obs ~ N(mu, 1)]

model.free_RVs

[mu ~ N(0, 1)]

model.observed_RVs

[obs ~ N(mu, 1)]

model.compile_logp()({"mu": 0})

array(-143.03962875)

值得强调的是我们在logp中做出的设计选择。如上所示，logp正在被调用并传递参数，因此它是模型实例的一个方法。更准确地说，它根据模型的当前状态或作为logp参数给出的状态组合一个函数（见下面的示例）。

由于多种原因，我们假设一个Model实例不是静态的。如果你需要在内部循环中使用logp并且它需要是静态的，只需使用类似logp = model.logp的方式。下面是一个示例——注意缓存效果和速度提升：

%timeit model.compile_logp()({"mu": 0.1})
logp = model.compile_logp()
%timeit logp({"mu": 0.1})

83 ms ± 7.1 ms per loop (mean ± std. dev. of 7 runs, 10 loops each)
18 µs ± 276 ns per loop (mean ± std. dev. of 7 runs, 100,000 loops each)

2. 概率分布

每个概率程序都由观测到的和未观测到的随机变量（RVs）组成。观测到的随机变量通过似然分布定义，而未观测到的随机变量通过先验分布定义。在PyMC模块中，概率分布的结构如下所示：

分布

• pymc:api_distributions_continuous

• pymc:api_distributions_discrete

• pymc:api_distributions_multivariate

• pymc:api_distributions_mixture

• pymc:api_distributions_timeseries

• pymc:api_distributions_censored

• pymc:api_distributions_simulator

未观测的随机变量

每个未观察到的随机变量都有以下调用签名：名称（字符串），参数关键字参数。因此，可以在模型上下文中这样定义一个正态先验：

with pm.Model():
    x = pm.Normal("x", mu=0, sigma=1)

与模型一样，我们可以评估其对数概率：

pm.logp(x, 0).eval()

array(-0.91893853)

观察到的随机变量

观测到的RVs与未观测到的RVs定义方式相同，但需要将数据传递到observed关键字参数中：

with pm.Model():
    obs = pm.Normal("x", mu=0, sigma=1, observed=rng.standard_normal(100))

observed 支持列表、numpy.ndarray 和 pytensor 数据结构。

确定性转换

PyMC 允许你以各种方式自由地对随机变量进行代数运算：

with pm.Model():
    x = pm.Normal("x", mu=0, sigma=1)
    y = pm.Gamma("y", alpha=1, beta=1)
    plus_2 = x + 2
    summed = x + y
    squared = x**2
    sined = pm.math.sin(x)

尽管这些变换可以无缝工作，但它们的结果并不会自动存储。因此，如果你想跟踪一个变换后的变量，你必须使用pm.Deterministic：

with pm.Model():
    x = pm.Normal("x", mu=0, sigma=1)
    plus_2 = pm.Deterministic("x plus 2", x + 2)

请注意，plus_2 可以以与上述相同的方式使用，我们只是告诉 PyMC 为我们跟踪这个随机变量。

随机变量列表 / 高维随机变量

上面我们已经看到了如何创建标量随机变量。在许多模型中，我们希望有多个随机变量。用户有时会尝试创建随机变量列表，如下所示：

with pm.Model():
    # bad:
    x = [pm.Normal(f"x_{i}", mu=0, sigma=1) for i in range(10)]

这可以工作，但它很慢且不推荐使用。相反，我们可以使用坐标：

coords = {"cities": ["Santiago", "Mumbai", "Tokyo"]}
with pm.Model(coords=coords) as model:
    # good:
    x = pm.Normal("x", mu=0, sigma=1, dims="cities")

x 现在是一个长度为3的数组，并且这个数组中的每个变量都与一个标签相关联。这将使我们在查看结果时非常容易区分这3个不同的变量。我们可以对这个数组进行索引或进行线性代数运算：

with model:
    y = x[0] * x[1]  # indexing is supported
    x.dot(x.T)  # linear algebra is supported

初始化随机变量

尽管PyMC会自动初始化模型，但有时为随机变量（RVs）定义初始值是有帮助的。这可以通过initval关键字参数来实现：

with pm.Model(coords={"idx": np.arange(5)}) as model:
    x = pm.Normal("x", mu=0, sigma=1, dims="idx")

model.initial_point()

{'x': array([0., 0., 0., 0., 0.])}

with pm.Model(coords={"idx": np.arange(5)}) as model:
    x = pm.Normal("x", mu=0, sigma=1, dims="idx", initval=rng.standard_normal(5))

model.initial_point()

{'x': array([-0.36012097, -0.16168135,  1.07485641, -0.08855632, -0.03857412])}

当尝试识别模型规范或初始化中的问题时，这种技术有时很有用。

3. 推理

一旦我们定义了模型，我们必须进行推理以近似后验分布。PyMC 支持两种广泛的推理方法：采样和变分推理。

3.1 采样

MCMC采样算法的主要入口是通过pm.sample()函数。默认情况下，此函数会尝试自动分配正确的采样器。pm.sample()返回一个arviz.InferenceData对象。InferenceData对象可以轻松地从文件中保存/加载，并且可以携带额外的（元）数据，如日期/版本和后验预测样本。查看ArviZ快速入门以了解更多信息。

with pm.Model() as model:
    mu = pm.Normal("mu", mu=0, sigma=1)
    obs = pm.Normal("obs", mu=mu, sigma=1, observed=rng.standard_normal(100))

    idata = pm.sample(2000)

Auto-assigning NUTS sampler...
Initializing NUTS using jitter+adapt_diag...
Multiprocess sampling (2 chains in 2 jobs)
NUTS: [mu]

100.00% [6000/6000 00:03<00:00 Sampling 2 chains, 0 divergences]

Sampling 2 chains for 1_000 tune and 2_000 draw iterations (2_000 + 4_000 draws total) took 4 seconds.

如您所见，对于仅包含连续变量的模型，PyMC 会分配 NUTS 采样器，即使在复杂模型中也非常高效。PyMC 还会运行初始调整以找到采样器的好起点参数。这里我们从后验中抽取 2000 个样本，并允许采样器在额外的 1500 次迭代中调整其参数。

如果没有通过 chains 参数设置，链的数量将根据可用 CPU 核心的数量来确定。

idata.posterior.dims

Frozen({'chain': 2, 'draw': 2000})

默认情况下，调优样本会被丢弃。通过设置discard_tuned_samples=False，它们可以被保留，并最终出现在InferenceData对象中的一个单独的组中（即，idata.warmup_posterior）。

您可以使用 chains 和 cores 参数来控制链的并行运行方式：

with pm.Model() as model:
    mu = pm.Normal("mu", mu=0, sigma=1)
    obs = pm.Normal("obs", mu=mu, sigma=1, observed=rng.standard_normal(100))

    idata = pm.sample(cores=4, chains=6)

Auto-assigning NUTS sampler...
Initializing NUTS using jitter+adapt_diag...
Multiprocess sampling (6 chains in 4 jobs)
NUTS: [mu]

100.00% [12000/12000 00:07<00:00 Sampling 6 chains, 0 divergences]

Sampling 6 chains for 1_000 tune and 1_000 draw iterations (6_000 + 6_000 draws total) took 7 seconds.

idata.posterior["mu"].shape

(6, 1000)

# get values of a single chain
idata.posterior["mu"].sel(chain=2).shape

(1000,)

3.2 分析采样结果

分析采样结果时最常用的图是所谓的轨迹图：

with pm.Model() as model:
    mu = pm.Normal("mu", mu=0, sigma=1)
    sd = pm.HalfNormal("sd", sigma=1)
    obs = pm.Normal("obs", mu=mu, sigma=sd, observed=rng.standard_normal(100))

    idata = pm.sample()

Auto-assigning NUTS sampler...
Initializing NUTS using jitter+adapt_diag...
Multiprocess sampling (2 chains in 2 jobs)
NUTS: [mu, sd]

100.00% [4000/4000 00:03<00:00 Sampling 2 chains, 0 divergences]

Sampling 2 chains for 1_000 tune and 1_000 draw iterations (2_000 + 2_000 draws total) took 4 seconds.

az.plot_trace(idata);

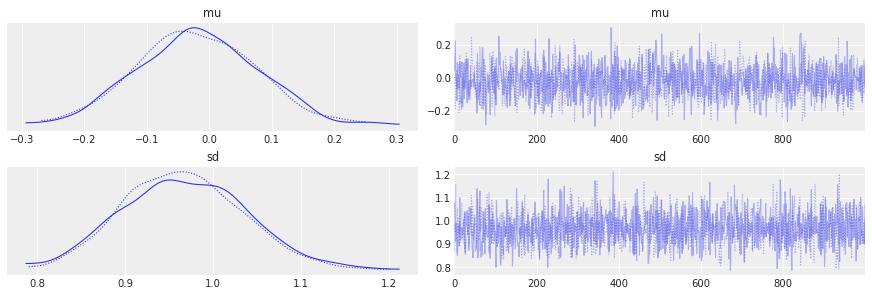
另一个常见的指标是Gelman-Rubin统计量，或R-hat：

az.summary(idata)

	mean	sd	hdi_3%	hdi_97%	mcse_mean	mcse_sd	ess_bulk	ess_tail	r_hat
mu	-0.019	0.096	-0.193	0.163	0.002	0.002	1608.0	1343.0	1.0
sd	0.967	0.069	0.835	1.089	0.002	0.001	1836.0	1406.0	1.0

R-hat 也作为 az.plot_forest 的一部分呈现：

az.plot_forest(idata, r_hat=True);

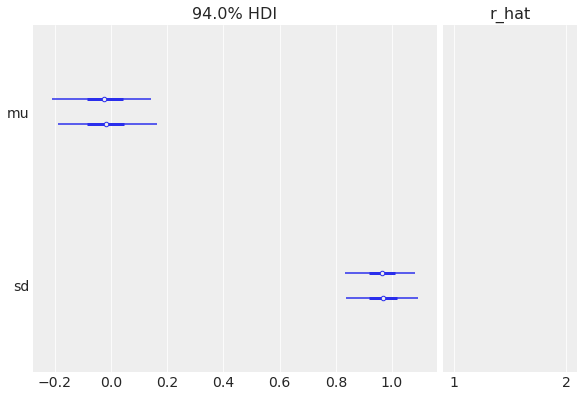
最后，对于受[Kruschke, 2014]启发的后验图，您可以使用：

az.plot_posterior(idata);

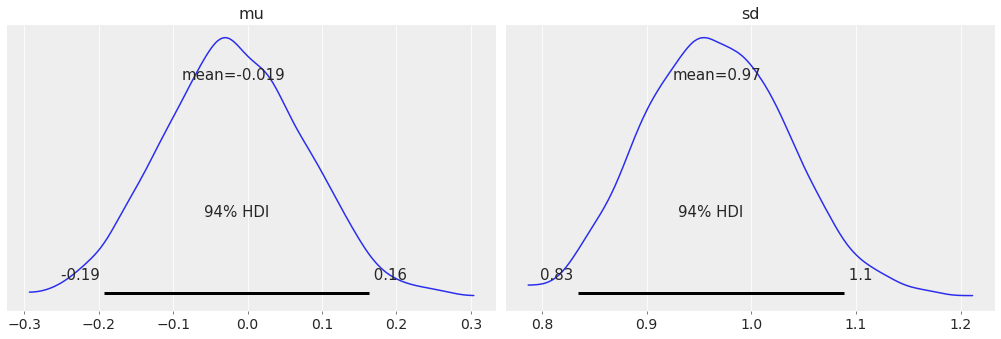
对于高维模型，查看所有参数的轨迹变得繁琐。当使用NUTS时，我们可以查看能量图来评估收敛问题：

with pm.Model(coords={"idx": np.arange(100)}) as model:
    x = pm.Normal("x", mu=0, sigma=1, dims="idx")
    idata = pm.sample()

az.plot_energy(idata);

Auto-assigning NUTS sampler...
Initializing NUTS using jitter+adapt_diag...
Multiprocess sampling (2 chains in 2 jobs)
NUTS: [x]

100.00% [4000/4000 00:04<00:00 Sampling 2 chains, 0 divergences]

Sampling 2 chains for 1_000 tune and 1_000 draw iterations (2_000 + 2_000 draws total) took 5 seconds.

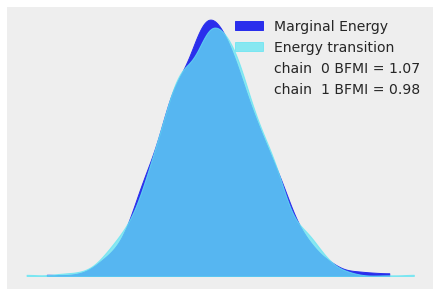
有关采样器统计信息和能量图的更多信息，请参阅采样器统计信息。有关识别采样问题及其解决方法的更多信息，请参阅使用分歧诊断偏差推理。

3.3 变分推断

PyMC 支持各种变分推断技术。虽然这些方法速度更快，但它们通常也准确性较低，并且可能导致有偏的推断。主要的入口点是 pymc.fit()。

with pm.Model() as model:
    mu = pm.Normal("mu", mu=0, sigma=1)
    sd = pm.HalfNormal("sd", sigma=1)
    obs = pm.Normal("obs", mu=mu, sigma=sd, observed=rng.standard_normal(100))

    approx = pm.fit()

100.00% [10000/10000 00:00<00:00 Average Loss = 142.01]

Finished [100%]: Average Loss = 142

返回的 Approximation 对象具有多种功能，例如从近似后验中抽取样本，我们可以像常规采样运行一样对其进行分析：

idata = approx.sample(1000)
az.summary(idata)

arviz - WARNING - Shape validation failed: input_shape: (1, 1000), minimum_shape: (chains=2, draws=4)

	mean	sd	hdi_3%	hdi_97%	mcse_mean	mcse_sd	ess_bulk	ess_tail	r_hat
mu	-0.023	0.169	-0.338	0.296	0.005	0.004	973.0	880.0	NaN
sd	0.989	0.158	0.694	1.262	0.005	0.004	972.0	1026.0	NaN

The variational 子模块提供了很大的灵活性，可以选择使用哪种变分推断（VI），并遵循面向对象的设计。例如，全秩ADVI估计一个完整的协方差矩阵：

mu = pm.floatX([0.0, 0.0])
cov = pm.floatX([[1, 0.5], [0.5, 1.0]])
with pm.Model(coords={"idx": np.arange(2)}) as model:
    pm.MvNormal("x", mu=mu, cov=cov, dims="idx")
    approx = pm.fit(method="fullrank_advi")

100.00% [10000/10000 00:03<00:00 Average Loss = 0.013113]

Finished [100%]: Average Loss = 0.012772

使用面向对象接口的等效表达式是：

with pm.Model(coords={"idx": np.arange(2)}) as model:
    pm.MvNormal("x", mu=mu, cov=cov, dims="idx")
    approx = pm.FullRankADVI().fit()

100.00% [10000/10000 00:03<00:00 Average Loss = 0.020591]

Finished [100%]: Average Loss = 0.020531

with pm.Model(coords={"idx": np.arange(2)}) as model:
    pm.MvNormal("x", mu=mu, cov=cov, dims="idx")
    approx = pm.FullRankADVI().fit()

100.00% [10000/10000 00:03<00:00 Average Loss = 0.014234]

Finished [100%]: Average Loss = 0.014143

plt.figure()
idata = approx.sample(10000)
az.plot_pair(idata, var_names="x", coords={"idx": [0, 1]});

<Figure size 432x288 with 0 Axes>

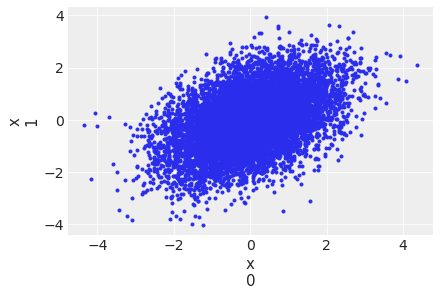
Stein变分梯度下降（SVGD）使用粒子来估计后验分布：

w = pm.floatX([0.2, 0.8])
mu = pm.floatX([-0.3, 0.5])
sd = pm.floatX([0.1, 0.1])
with pm.Model() as model:
    pm.NormalMixture("x", w=w, mu=mu, sigma=sd)
    approx = pm.fit(method=pm.SVGD(n_particles=200, jitter=1.0))

100.00% [10000/10000 01:20<00:00]

with pm.Model() as model:
    pm.NormalMixture("x", w=[0.2, 0.8], mu=[-0.3, 0.5], sigma=[0.1, 0.1])

plt.figure()
idata = approx.sample(10000)
az.plot_dist(idata.posterior["x"]);

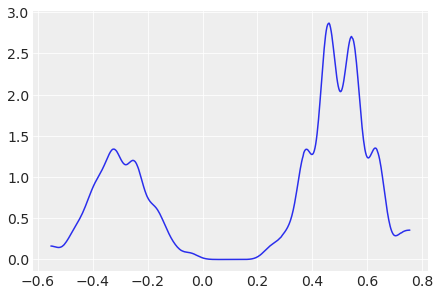
有关变分推断的更多信息，请参阅变分推断。

4. 后验预测采样

函数 sample_posterior_predictive() 对保留数据进行预测并执行后验预测检查。

data = rng.standard_normal(100)
with pm.Model() as model:
    mu = pm.Normal("mu", mu=0, sigma=1)
    sd = pm.HalfNormal("sd", sigma=1)
    obs = pm.Normal("obs", mu=mu, sigma=sd, observed=data)

    idata = pm.sample()

Auto-assigning NUTS sampler...
Initializing NUTS using jitter+adapt_diag...
Multiprocess sampling (2 chains in 2 jobs)
NUTS: [mu, sd]

100.00% [4000/4000 00:03<00:00 Sampling 2 chains, 0 divergences]

Sampling 2 chains for 1_000 tune and 1_000 draw iterations (2_000 + 2_000 draws total) took 4 seconds.

with model:
    idata.extend(pm.sample_posterior_predictive(idata))

100.00% [2000/2000 00:00<00:00]

fig, ax = plt.subplots()
az.plot_ppc(idata, ax=ax)
ax.axvline(data.mean(), ls="--", color="r", label="True mean")
ax.legend(fontsize=10);

/home/xian/anaconda3/envs/pymc-dev-py39/lib/python3.9/site-packages/IPython/core/pylabtools.py:151: UserWarning: Creating legend with loc="best" can be slow with large amounts of data.
  fig.canvas.print_figure(bytes_io, **kw)

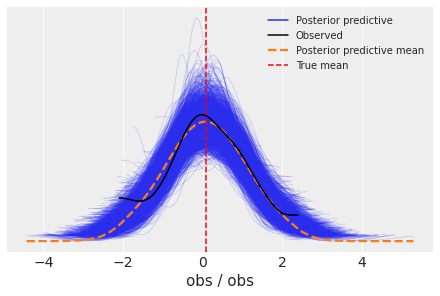
4.1 对保留数据的预测

在许多情况下，您希望对未见过的/保留的数据进行预测。这在概率机器学习和贝叶斯深度学习中尤为重要。PyMC 包含一个 pm.MutableData 容器，以帮助实现这些用途。它是一个围绕 pytensor.shared 变量的包装器，并允许稍后更改数据的值。否则，pm.MutableData 对象可以像任何其他 numpy 数组或张量一样使用。

这一区别非常重要，因为PyMC中的所有模型在内部都是巨大的符号表达式。当你直接将原始数据传递到模型中时，你实际上是允许PyTensor将这些数据视为常量，并在这样做有意义的情况下对其进行优化。如果你以后需要更改这些数据，你可能无法在更大的符号表达式中指向它。使用pm.MutableData提供了一种在符号表达式中指向特定位置并更改其内容的方法。

x = rng.standard_normal(100)
y = x > 0

coords = {"idx": np.arange(100)}
with pm.Model() as model:
    # create shared variables that can be changed later on
    x_obs = pm.MutableData("x_obs", x, dims="idx")
    y_obs = pm.MutableData("y_obs", y, dims="idx")

    coeff = pm.Normal("x", mu=0, sigma=1)
    logistic = pm.math.sigmoid(coeff * x_obs)
    pm.Bernoulli("obs", p=logistic, observed=y_obs, dims="idx")
    idata = pm.sample()

Auto-assigning NUTS sampler...
Initializing NUTS using jitter+adapt_diag...
Multiprocess sampling (2 chains in 2 jobs)
NUTS: [x]

100.00% [4000/4000 00:03<00:00 Sampling 2 chains, 0 divergences]

Sampling 2 chains for 1_000 tune and 1_000 draw iterations (2_000 + 2_000 draws total) took 3 seconds.

现在假设我们要对未见过的数据进行预测。为此，我们需要更改 x_obs 和 y_obs 的值。理论上我们不需要设置 y_obs，因为我们想要预测它，但它必须与 x_obs 的形状相匹配。

with model:
    # change the value and shape of the data
    pm.set_data(
        {
            "x_obs": [-1, 0, 1.0],
            # use dummy values with the same shape:
            "y_obs": [0, 0, 0],
        },
        coords={"idx": [1001, 1002, 1003]},
    )

    idata.extend(pm.sample_posterior_predictive(idata))

100.00% [2000/2000 00:00<00:00]

idata.posterior_predictive["obs"].mean(dim=["draw", "chain"])

<xarray.DataArray 'obs' (idx: 3)>
array([0.0215, 0.488 , 0.982 ])
Coordinates:
  * idx      (idx) int64 1001 1002 1003

xarray.DataArray

'obs'

• idx: 3

• 0.0215 0.488 0.982

  array([0.0215, 0.488 , 0.982 ])

• Coordinates: (1)
  • idx
    (idx)
    int64
    1001 1002 1003

    array([1001, 1002, 1003])

• Attributes: (0)

参考资料

[1]

约翰·克鲁施克。贝叶斯数据分析：R、JAGS和Stan的教程。学术出版社，2014年。

%load_ext watermark
%watermark -n -u -v -iv -w -p pytensor,aeppl,xarray

Last updated: Fri Jun 03 2022

Python implementation: CPython
Python version       : 3.9.13
IPython version      : 8.4.0

pytensor: 2.6.2
aeppl : 0.0.31
xarray: 2022.3.0

arviz     : 0.12.1
numpy     : 1.22.4
pymc      : 4.0.0b6
pytensor    : 2.6.2
matplotlib: 3.5.2

Watermark: 2.3.1