空间数据的Besag-York-Mollie模型#
import os
import arviz as az
import matplotlib.pyplot as plt
import numpy as np
import pandas as pd
import pymc as pm
import pytensor.tensor as pt
from scipy import sparse
from scipy.linalg import solve
from scipy.sparse.linalg import spsolve
# these libraries are not dependencies of pymc
import networkx as nx
import nutpie
RANDOM_SEED = 8926
rng = np.random.default_rng(RANDOM_SEED)
az.style.use("arviz-darkgrid")
为什么要使用Besag-York-Mollie模型?#
本笔记本解释了为什么以及如何在PyMC中部署Besag-York-Mollie(BYM)模型。BYM模型是许多空间统计问题的有吸引力的方法。它很灵活——一旦你添加了BYM组件,其余的工作流程就像任何其他贝叶斯广义线性模型一样进行。你可以添加预测因子来估计因果效应。你可以更换链接函数和结果分布来处理不同的数据类型。你可以混合和匹配最适合的采样器。
BYM 也能很好地处理大型数据集。空间模型的一个常见问题是,随着数据集大小的增加,其计算成本会迅速增长。例如,PyMC 的 CAR 模型 就是如此。而使用 BYM 模型,计算成本的增长几乎是线性的。
BYM 模型适用于处理 区域 数据,例如相邻的州、县或人口普查区。对于涉及空间点或连续距离度量的问题,请考虑使用 高斯过程。
由ICAR提供支持#
驱动BYM模型的主要引擎是内在条件自回归先验(ICAR)。ICAR是一种特殊的多变量正态分布,假设相邻区域具有协变性。
在讨论空间建模时,采用一些图论的词汇会有所帮助。图由节点和边组成。节点代表空间中的区域,而边代表邻近关系。在这种类型的问题中,我们在共享边界的两个区域之间绘制一条边。
假设我们有一个图,类似于从邻接矩阵 W 构建的图。
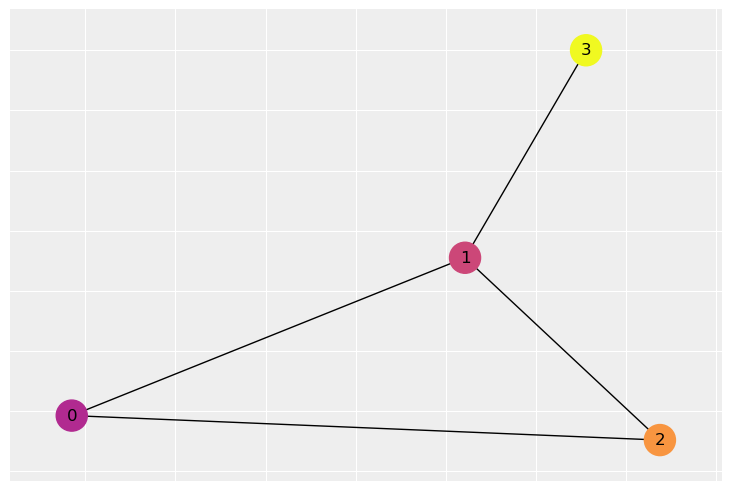
邻接矩阵编码了哪些节点与其他节点相连。如果节点i和j相连,那么在第i行第j列将有一个1。否则,将有一个零。例如,节点1和3相连。在矩阵的第3行第1列有一个1。然而,节点3与节点2不相连,所以在第3行第2列有一个0。当然,我们必须记住python的索引。第一行是0,最后一行是3。邻接矩阵也是对称的——如果加拿大与美国相邻,那么美国也与加拿大相邻。
ICAR的密度函数接受一个邻接矩阵 W 和一个方差 \(\sigma\)。我们通常假设 \(\sigma = 1\) 并通过其他方式处理方差,因此我暂时忽略第一个分数。
每个\(\phi_{i}\) 根据其与每个邻居的平方距离进行惩罚。符号 \(i \sim j\) 表示对 \(\phi_{i}\) 的所有邻居求和。
因此,例如,假设颜色的强度表示每个节点上变量的值。节点1与所有节点相连。节点1和节点0的颜色相当相似,因此惩罚会很小。但节点2的颜色与节点1非常不同,因此会受到较大的惩罚。如果我们把注意力转向节点3,它只有一个邻居,并且会根据与节点1的距离收到一个较大的惩罚。
通过这种方式,ICAR编码了空间统计的核心假设 - 相邻区域应比远距离区域更相似。最可能的结果是一个图中每个节点具有相同值的图。在这种情况下,相邻节点之间的平方距离始终为零。图中相邻区域之间的变化越突然,对数密度越低。
ICAR 有其他一些特殊功能:它是受约束的,因此所有 \(\phi\) 的总和为零。这也意味着 \(\phi\) 的平均值为零。将 ICAR 值视为类似于 z 分数可能会有所帮助。它们表示以 0 为中心的相对偏差。ICAR 通常也仅用作较大模型的一个子组件。模型的其他部分通常会调整尺度(通过方差参数)或位置(通过截距参数)。关于 ICAR 背后的数学及其与 CAR 的关系的易懂讨论可以在这里找到,或者在学术论文版本中找到 [Morris 等,2019]。
随机效应的灵活性#
统计建模的典型目标之一是将数据的方差划分为三类:由感兴趣的原因解释的方差、结构化方差和非结构化方差。在我们的例子中,ICAR模型旨在捕捉(空间上)结构化的方差。添加预测变量可以处理第一类。BYM模型通过随机效应\(\theta\)来处理第三类。随机效应是一个长度为n的随机变量向量,其中n是区域的数目。它旨在捕捉所有未被空间或因果效应解释的剩余方差。
构建一个包含结构化和非结构化方差的模型可能会很棘手。天真的方法通常会遇到可识别性的问题。每个组件原则上都可以独立解释方差。因此,拟合算法可能无法在参数空间中稳定到一个小的邻域。
BYM模型经过精心设计,用于解决可识别性问题。它使用混合分布,其中参数\(\rho\)控制结构化方差与非结构化方差的平衡。BYM模型的形式如下:
当 \(\rho\) 接近1时,大部分方差是空间结构化的。当 \(\rho\) 接近0时,大部分方差是无结构的。
\(\sigma\) 是一个由 \(\theta\) 和 \(\phi\) 共享的尺度参数。\(\theta\) 和 \(\phi\) 都以零为中心,并且方差为1。因此,它们都像z分数一样起作用。\(\sigma\) 可以拉伸或收缩效应的混合,因此适合实际数据。\(\beta\) 是一个共享的截距,它将混合重新居中以适应数据。最后,\(\text{s}\) 是缩放因子。它是一个从邻接矩阵计算出的常数。它重新调整了 \(\phi\) 的尺度,使它们具有与 \(\theta\) 相同的预期方差。关于为什么这有效的更详细讨论 如下所示。
拟合此模型解决了将方差划分为结构性和非结构性成分的挑战。剩下的唯一挑战是确定预测变量,这一挑战因情况而异。Riebler et al. [2016]提出了这种特定的BYM模型方法,并提供了更多关于为什么这种BYM模型的参数化既可解释又可识别的解释,而之前的BYM模型参数化通常并非如此。
在纽约市行人事故数据集上展示BYM模型#
我们将在一个记录纽约市涉及行人的交通事故数量的数据集上演示BYM模型。数据被组织成大约2000个普查区,提供了我们的空间结构。我们的目标是展示我们可以将方差分解为解释性、空间结构性和非结构性的组成部分。
设置数据#
空间数据以边列表的形式呈现。除了邻接矩阵外,边列表是另一种在计算机上表示区域数据的流行技术。边列表是一对列表,用于存储有关图中边的信息。假设i和j是两个节点的名称。如果节点i和节点j相连,那么一个列表将包含i,另一个列表将在同一行中包含j。例如,在下方的数据框中,节点1与节点1452以及节点1721相连。
try:
df_edges = pd.read_csv(os.path.join("..", "data", "nyc_edgelist.csv"))
except FileNotFoundError:
df_edges = pd.read_csv(pm.get_data("nyc_edgelist.csv"))
df_edges
| N | N_edges | node1 | node2 | |
|---|---|---|---|---|
| 0 | 1921 | 5461 | 1 | 1452 |
| 1 | 1921 | 5461 | 1 | 1721 |
| 2 | 1921 | 5461 | 2 | 3 |
| 3 | 1921 | 5461 | 2 | 4 |
| 4 | 1921 | 5461 | 2 | 5 |
| ... | ... | ... | ... | ... |
| 5456 | 1921 | 5461 | 1918 | 1919 |
| 5457 | 1921 | 5461 | 1918 | 1921 |
| 5458 | 1921 | 5461 | 1919 | 1920 |
| 5459 | 1921 | 5461 | 1919 | 1921 |
| 5460 | 1921 | 5461 | 1920 | 1921 |
5461 行 × 4 列
然而,要真正运行我们的模型,我们需要将边列表转换为邻接矩阵。下面的代码执行了这一任务以及其他一些清理任务。
# convert edgelist to adjacency matrix
# extract and reformat the edgelist
nodes = np.stack((df_edges.node1.values, df_edges.node2.values))
nodes = nodes.T
# subtract one for python indexing
nodes = nodes - 1
# convert the number of nodes to a integer
N = int(df_edges.N.values[0])
# build a matrix of zeros to store adjacency
# it has size NxN where N is the number of
# areas in the dataset
adj = np.zeros((N, N))
# loop through the edgelist and assign 1
# to the location in the adjacency matrix
# to represent the edge
# this will only fill in the upper triangle
# of the matrix
for node in nodes:
adj[tuple(node)] = 1
# add the transpose to make the adjacency
# matrix symmetrical
W_nyc = adj.T + adj
我们将计算缩放因子。这需要一个相当复杂的特殊函数。对该函数的详细解释会使我们偏离纽约市案例研究的讨论,因此我将把缩放因子的讨论留到后面。
def scaling_factor_sp(A):
"""Compute the scaling factor from an adjacency matrix.
This function uses sparse matrix computations and is most
efficient on sparse adjacency matrices. Used in the BYM2 model.
The scaling factor is a measure of the variance in the number of
edges across nodes in a connected graph.
Only works for fully connected graphs. The argument for scaling
factors is developed by Andrea Riebler, Sigrunn H. Sørbye,
Daniel Simpson, Havard Rue in "An intuitive Bayesian spatial
model for disease mapping that accounts for scaling"
https://arxiv.org/abs/1601.01180"""
# Computes the precision matrix in sparse format
# from an adjacency matrix.
num_neighbors = A.sum(axis=1)
A = sparse.csc_matrix(A)
D = sparse.diags(num_neighbors, format="csc")
Q = D - A
# add a small jitter along the diagonal
Q_perturbed = Q + sparse.diags(np.ones(Q.shape[0])) * max(Q.diagonal()) * np.sqrt(
np.finfo(np.float64).eps
)
# Compute a version of the pseudo-inverse
n = Q_perturbed.shape[0]
b = sparse.identity(n, format="csc")
Sigma = spsolve(Q_perturbed, b)
A = np.ones(n)
W = Sigma @ A.T
Q_inv = Sigma - np.outer(W * solve(A @ W, np.ones(1)), W.T)
# Compute the geometric mean of the diagonal on a
# precision matrix.
return np.exp(np.sum(np.log(np.diag(Q_inv))) / n)
scaling_factor = scaling_factor_sp(W_nyc)
scaling_factor
0.7136574058611103
第一个.csv文件仅包含空间结构部分。其余的数据是单独提供的——这里我们将引入事故数量y和人口普查区的规模,E。我们将使用人口规模作为偏移量——我们应该预期人口较多的地区会因为一些琐碎的原因发生更多的事故。更有趣的是与某个地区相关的超额风险。
最后,我们还将探讨一个预测变量,即社会碎片化指数。该指数由空置住房单元数量、独居人口、租房者和在过去一年内搬家的人的测量值构成。这些社区往往较少整合,社会支持系统较弱。社会流行病学界对生态变量如何渗透到公共健康的各个方面感兴趣。因此,我们将探讨社会碎片化是否能解释交通事故的模式。该指标已标准化,均值为零,标准差为1。
try:
df_nyc = pd.read_csv(os.path.join("..", "data", "nyc_traffic.csv"))
except FileNotFoundError:
df_nyc = pd.read_csv(pm.get_data("nyc_traffic.csv"))
y = df_nyc.events_2001.values
E = df_nyc.pop_2001.values
fragment_index = df_nyc.fragment_index.values
# Most census tracts have huge populations
# but a handful have 0. We round
# those up to 10 to avoid triggering an error
# with the log of 0.
E[E < 10] = 10
log_E = np.log(E)
area_idx = df_nyc["census_tract"].values
coords = {"area_idx": area_idx}
通过可视化邻接矩阵,我们可以了解空间结构。下图仅捕捉了人口普查轨道的相对位置。它不考虑绝对位置,因此看起来不像纽约市。这种表示突出了城市由几个均匀连接的区域组成,几个中心枢纽拥有大量的连接,然后是几个狭窄的走廊。
# build the positions of the nodes. We'll only
# generate the positions once so that we can
# compare visualizations from the data to
# the model predictions.
# I found that running spectral layout first
# and passing it to spring layout makes easy to read
# visualizations for large datasets.
G_nyc = nx.Graph(W_nyc)
pos = nx.spectral_layout(G_nyc)
pos = nx.spring_layout(G_nyc, pos=pos, seed=RANDOM_SEED)
# the spread of the data is pretty high. Most areas have 0 accidents.
# one area has 300. Color-gradient based visualization doesn't work
# well under those conditions. So for the purpose of the color
# we'll cap the accidents at 30 using vmax
#
# however, we'll also make the node size sensitive to the real
# number of accidents. So big yellow nodes have way more accidents
# than small yellow nodes.
plt.figure(figsize=(10, 8))
nx.draw_networkx(
G_nyc,
pos=pos,
node_color=y,
cmap="plasma",
vmax=30,
width=0.5,
alpha=0.6,
with_labels=False,
node_size=20 + 3 * y,
)
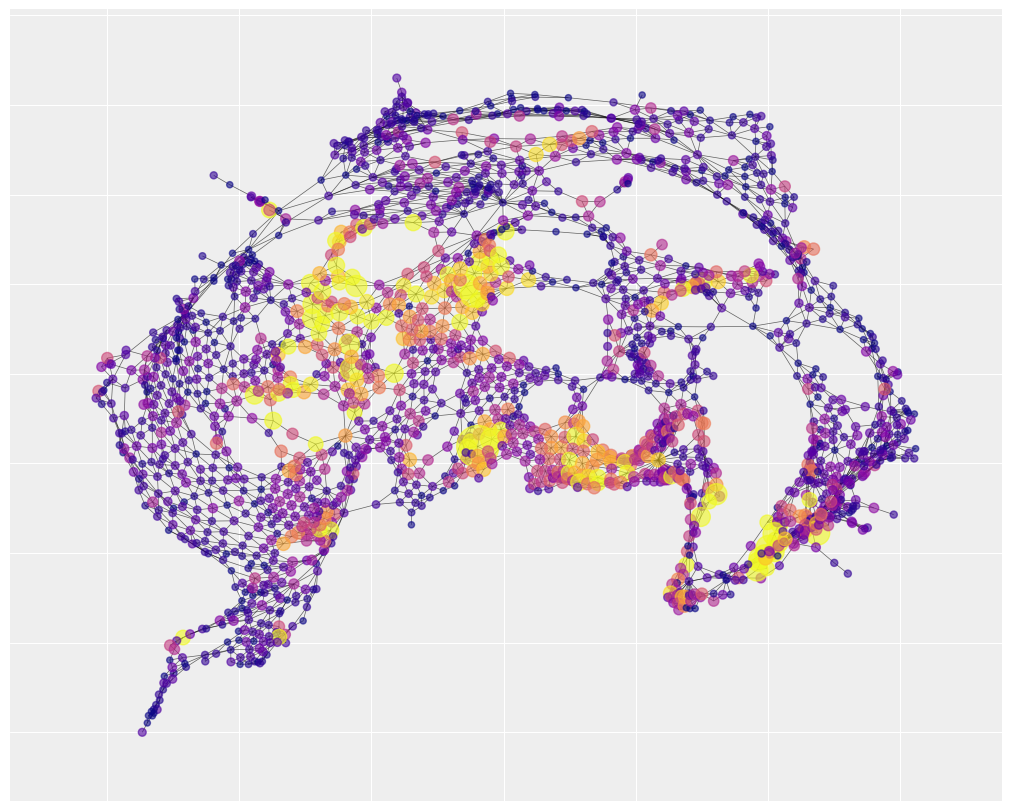
地图还显示了有许多热点区域,大部分事故都发生在这些地方,并且它们在空间上呈聚集分布,即右下角、底部中心和左中区域。这表明空间自相关模型是一个合适的选择。
我们还可以可视化社会碎片化的空间布局。你会注意到,有一个社会碎片化的社区与交通事故地图重叠。下面的统计分析将帮助我们了解这种重叠的真实强度。
plt.figure(figsize=(10, 8))
nx.draw_networkx(
G_nyc,
pos=pos,
node_color=fragment_index,
cmap="plasma",
width=0.5,
alpha=0.6,
with_labels=False,
node_size=40 + 5 * fragment_index,
)
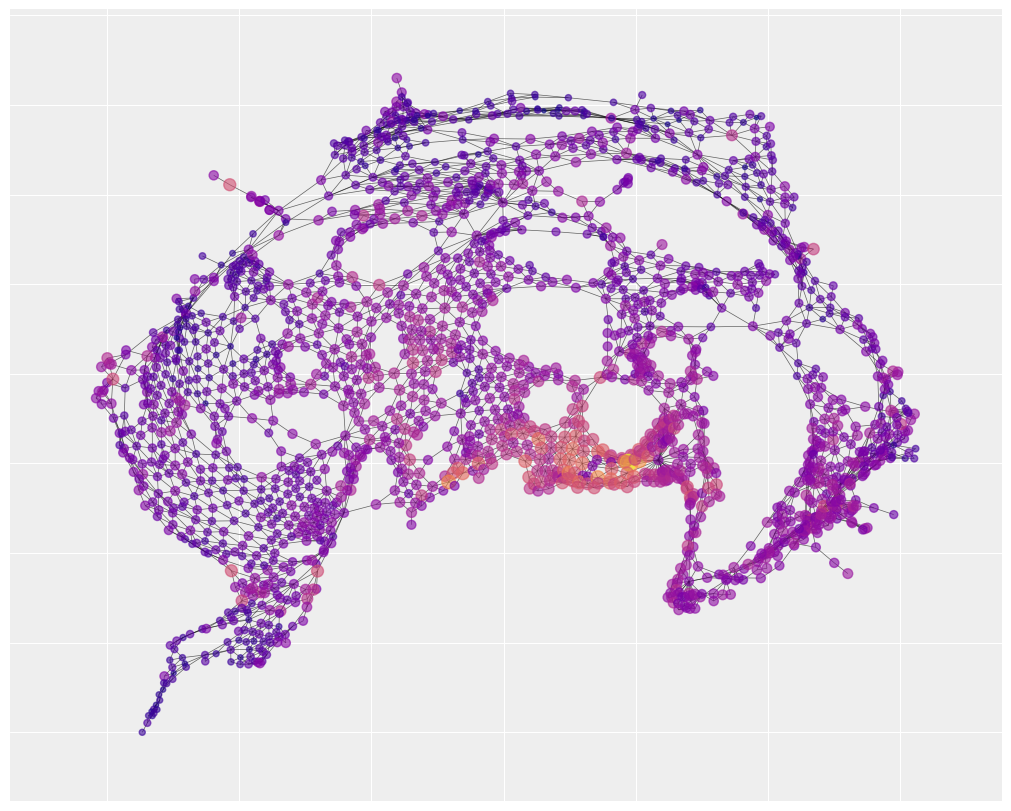
使用PyMC指定一个BYM模型#
BYM 的所有参数已经在 第 1 节 中介绍过了。现在只需要为它们分配一些先验。\(\theta\) 的先验比较挑剔——我们需要为其分配均值为 0 和标准差为 1,以便我们可以将其解释为与 \(\phi\) 相比较。否则,先验分布提供了结合领域专业知识的机会。在这个问题中,我将选择一些弱信息先验。
最后,我们将使用泊松结果分布。交通事故的数量是一个计数结果,最大可能值非常大。为了确保我们的预测保持为正数,我们将在将线性模型传递给泊松分布之前对其进行指数化处理。
with pm.Model(coords=coords) as BYM_model:
# intercept
beta0 = pm.Normal("beta0", 0, 1)
# fragmentation effect
beta1 = pm.Normal("beta1", 0, 1)
# independent random effect
theta = pm.Normal("theta", 0, 1, dims="area_idx")
# spatially structured random effect
phi = pm.ICAR("phi", W=W_nyc, dims="area_idx")
# joint variance of random effects
sigma = pm.HalfNormal("sigma", 1)
# the mixing rate is rho
rho = pm.Beta("rho", 0.5, 0.5)
# the bym component - it mixes a spatial and a random effect
mixture = pm.Deterministic(
"mixture", pt.sqrt(1 - rho) * theta + pt.sqrt(rho / scaling_factor) * phi, dims="area_idx"
)
# exponential link function to ensure
# predictions are positive
mu = pm.Deterministic(
"mu", pt.exp(log_E + beta0 + beta1 * fragment_index + sigma * mixture), dims="area_idx"
)
y_i = pm.Poisson("y_i", mu, observed=y)
采样模型#
# if you haven't installed nutpie, it's okay to to just delete
# 'nuts_sampler="nutpie"'. The default sampler took roughly 12 minutes on
# my machine.
with BYM_model:
idata = pm.sample(1000, nuts_sampler="nutpie", random_seed=rng)
采样器进度
总链数: 4
活跃链:0
完成的链: 4
采样时间为31秒
预计完成时间: now
| Progress | Draws | Divergences | Step Size | Gradients/Draw |
|---|---|---|---|---|
| 2000 | 0 | 0.13 | 255 | |
| 2000 | 0 | 0.13 | 127 | |
| 2000 | 0 | 0.13 | 63 | |
| 2000 | 0 | 0.13 | 63 |
我们可以通过几种方式评估采样器。首先,看起来我们所有的链都收敛了。所有参数的rhat值都非常接近1。
rhat = az.summary(idata, kind="diagnostics").r_hat.values
sum(rhat > 1.03)
0
其次,所有主要参数的轨迹图看起来是平稳且混合良好的。它们还揭示了rho的平均值大约在0.50左右,表明数据中可能存在空间效应。
az.plot_trace(idata, var_names=["beta0", "beta1", "sigma", "rho"])
plt.tight_layout();
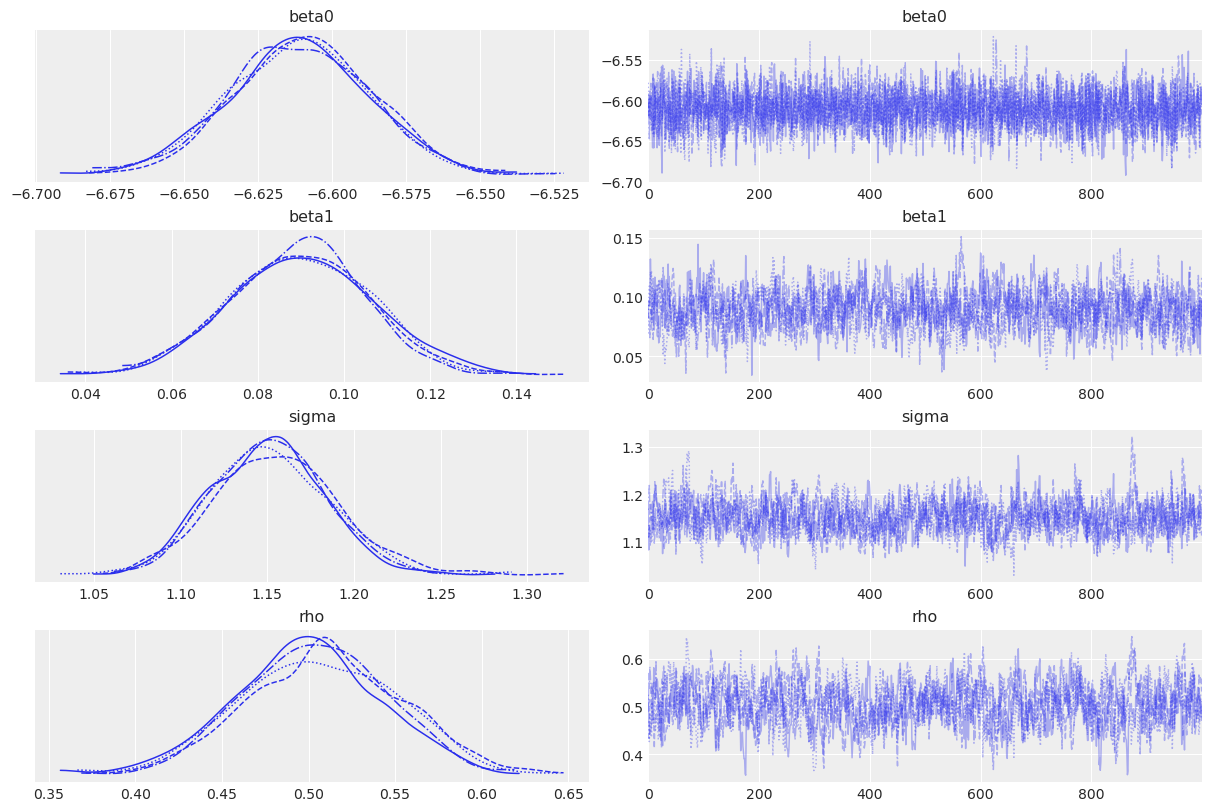
我们的轨迹图还表明,社会碎片化对交通事故有轻微影响,大部分后验质量介于0.06和0.12之间。
后验预测检查#
所有这些工作的成果是,我们现在可以直观地理解将方差分解为解释性、空间性和非结构化部分的意义。一种使这一点生动起来的方法是分别检查模型的每个组成部分。我们将看到如果空间效应是方差的唯一来源,模型认为纽约市应该是什么样子,然后我们将转向解释性效应,最后是随机效应。
在第一种情况下,我们将仅可视化来自模型的空间组件的预测。换句话说,我们假设 \(\rho = 1\) 并忽略 \(\theta\) 和社会碎片化。
然后我们将把我们的预测叠加到之前构建的邻接地图上。
# draw posterio
with pm.do(BYM_model, {"rho": 1.0, "beta1": 0}):
y_predict = pm.sample_posterior_predictive(
idata, var_names=["mu", "mixture"], predictions=True, extend_inferencedata=False
)
y_spatial_pred = y_predict.predictions.mu.mean(dim=["chain", "draw"]).values
plt.figure(figsize=(10, 8))
nx.draw_networkx(
G_nyc,
pos=pos,
node_color=y_spatial_pred,
cmap="plasma",
vmax=30,
width=0.5,
alpha=0.6,
with_labels=False,
node_size=20 + 3 * y_spatial_pred,
)
Sampling: []
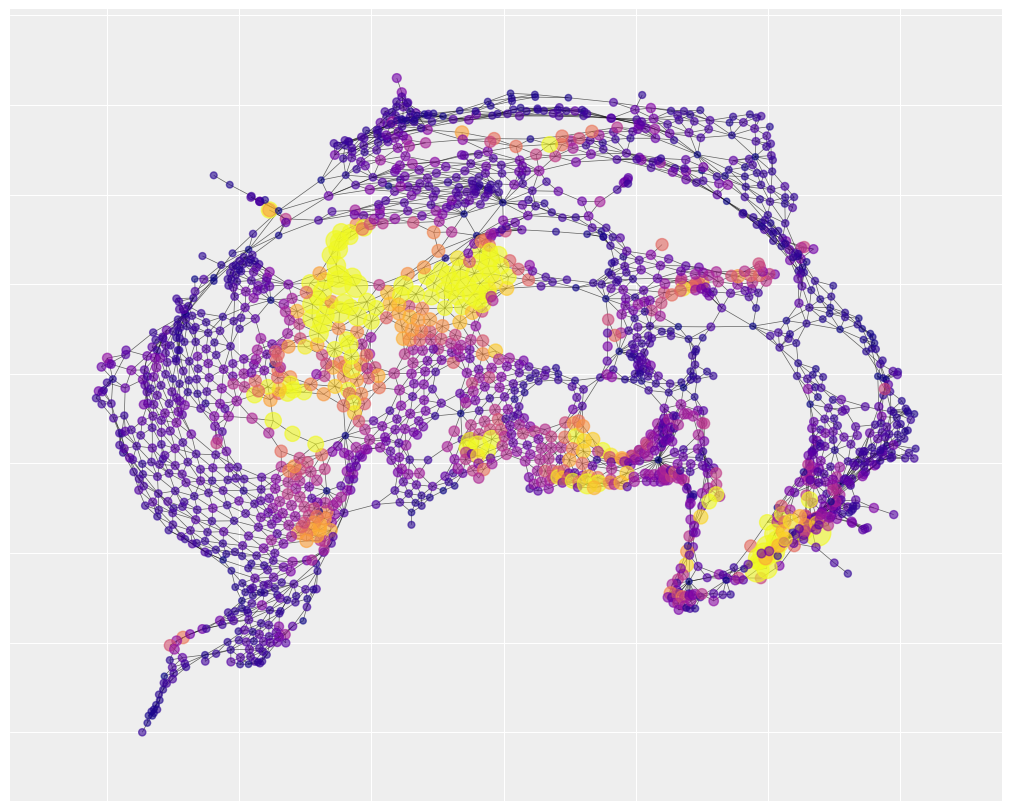
生成的图片称为空间平滑。附近的区域往往彼此非常相似,从而形成了明显的风险邻域。在深紫色区域,方差很小,预测的事故数量接近于零。
空间平滑对于预测特别有用。想象一下,在一个高事故率的社区中,有一个低事故率的区域。假设你想预测未来哪些地方会有高事故率,以便你可以针对这些区域进行干预。仅仅关注过去高事故率的环形区域可能是一个错误。中间的低事故率区域在过去可能只是运气好。在未来,该区域可能更接近其邻居的情况,而不是其过去的情况。空间平滑依赖于部分池化的相同原理——通过从附近区域汇集信息来纠正异常,我们可以学到更多。
我们可以注意到,有三个风险区域,由大的黄色集群表示,被很好地捕捉到了。这表明,许多交通事故的原因与未识别但空间结构化的因素有关。相比之下,社会分裂指数仅解释了地图底部中心的一个风险区域(在其他地方有一些小的成功区域)。
with pm.do(
BYM_model,
{
"sigma": 0.0,
},
):
y_predict = pm.sample_posterior_predictive(
idata, var_names=["mu", "mixture"], predictions=True, extend_inferencedata=False
)
y_frag_pred = y_predict.predictions.mu.mean(dim=["chain", "draw"]).values
plt.figure(figsize=(10, 8))
nx.draw_networkx(
G_nyc,
pos=pos,
node_color=y_frag_pred,
cmap="plasma",
vmax=30,
width=0.5,
alpha=0.6,
with_labels=False,
node_size=20 + 3 * y_frag_pred,
)
Sampling: []
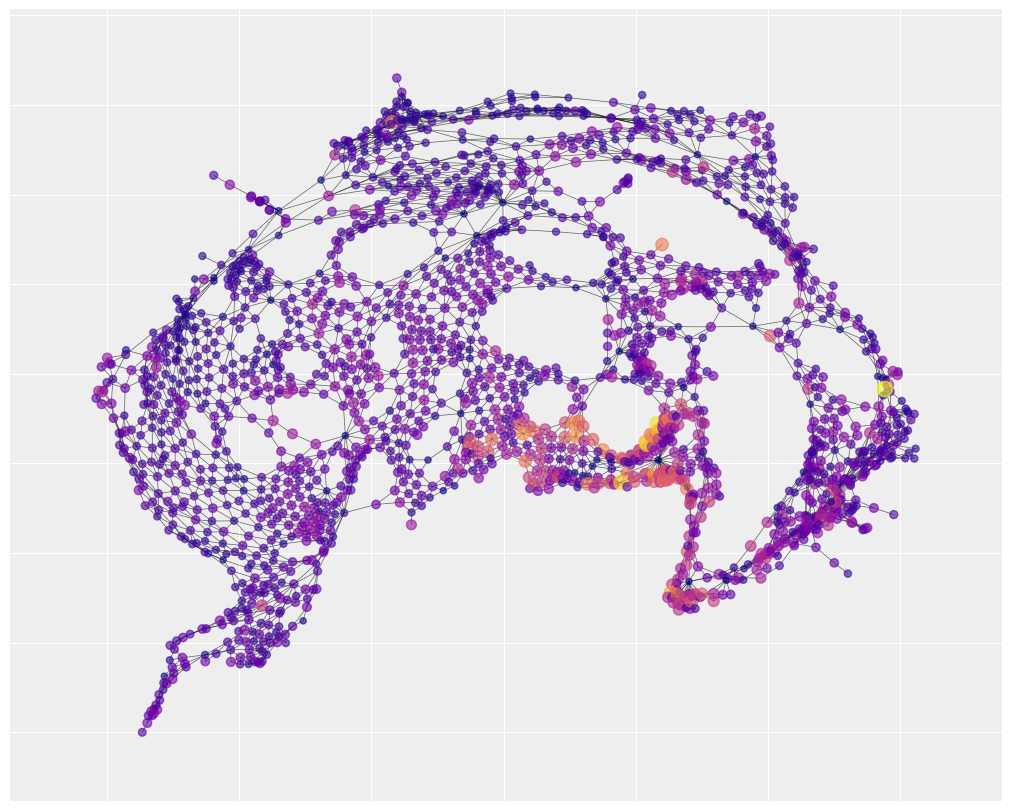
最后,我们可以通过假设 \(\rho = 0\) 来查看非结构化方差。如果我们的模型成功地划分了方差,那么在非结构化方差中应该不会留下太多的空间聚类。相反,方差应该分散在整个地图上。
with pm.do(BYM_model, {"rho": 0.0, "beta1": 0}):
y_predict = pm.sample_posterior_predictive(
idata, var_names=["mu", "mixture"], predictions=True, extend_inferencedata=False
)
y_unspatial_pred = y_predict.predictions.mu.mean(dim=["chain", "draw"]).values
plt.figure(figsize=(10, 8))
nx.draw_networkx(
G_nyc,
pos=pos,
node_color=y_unspatial_pred,
cmap="plasma",
vmax=30,
width=0.5,
alpha=0.6,
with_labels=False,
node_size=20 + 3 * y_unspatial_pred,
)
Sampling: []
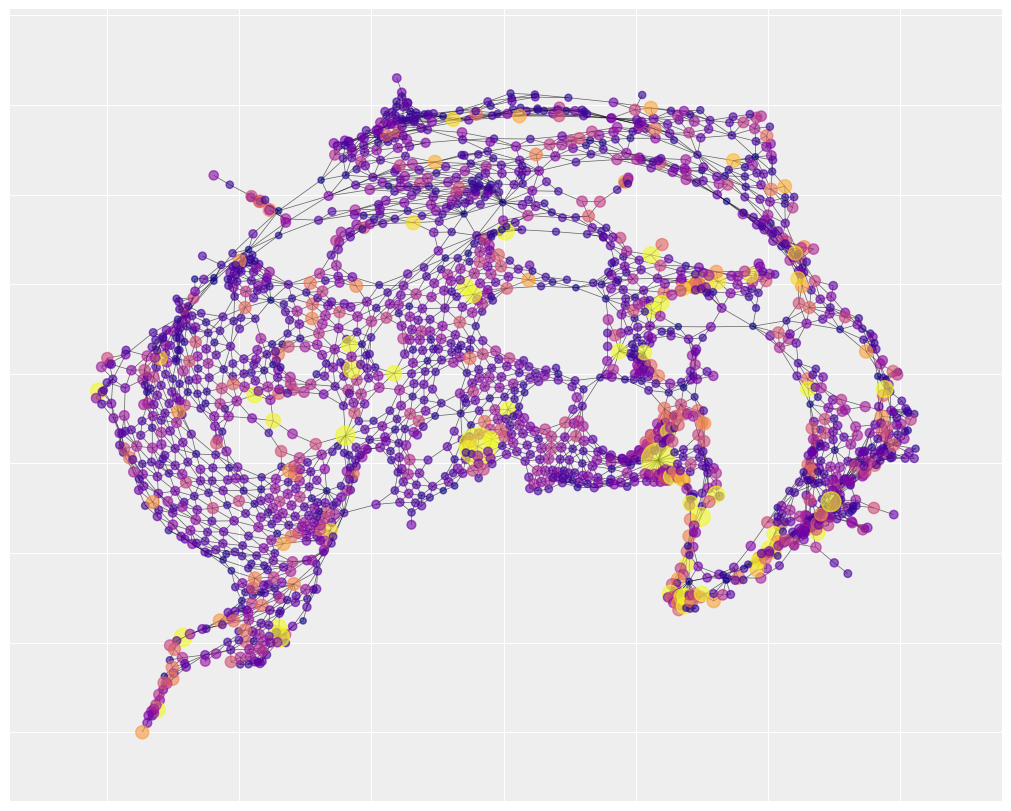
缩放因子实际上做了什么?#
关于BYM模型的讨论通常会省略对缩放因子的过多细节。这样做是有充分理由的。如果你的主要兴趣在于流行病学,你其实不需要了解它。用户可以将其视为一个黑箱。缩放因子的计算还涉及线性代数中一些相当晦涩的概念。我不会在这里讨论其计算过程,但我将尝试提供一些关于它在BYM模型中作用的直觉。
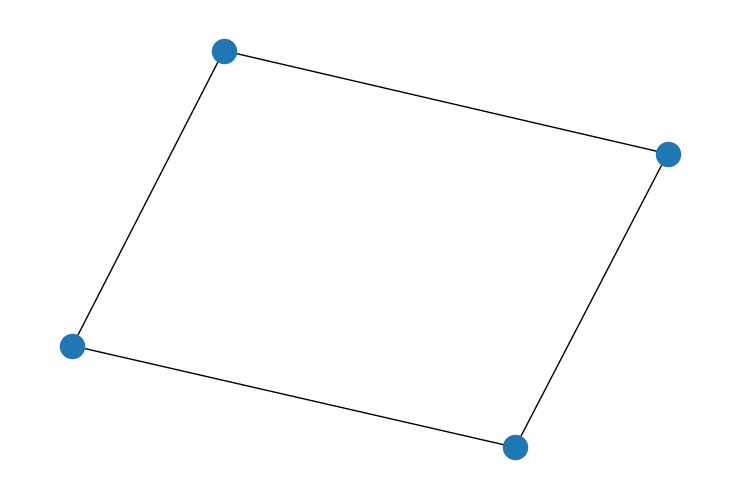
看看这两张图表。
W1 = np.array([[0, 1, 1, 0], [1, 0, 0, 1], [1, 0, 0, 1], [0, 1, 1, 0]])
G = nx.Graph(W1)
nx.draw(G)
c:\Users\dsaun\Anaconda3\envs\spatial_pymc_env\Lib\site-packages\IPython\core\events.py:89: UserWarning: There are no gridspecs with layoutgrids. Possibly did not call parent GridSpec with the "figure" keyword
func(*args, **kwargs)
c:\Users\dsaun\Anaconda3\envs\spatial_pymc_env\Lib\site-packages\IPython\core\pylabtools.py:152: UserWarning: There are no gridspecs with layoutgrids. Possibly did not call parent GridSpec with the "figure" keyword
fig.canvas.print_figure(bytes_io, **kw)
W2 = np.array([[0, 1, 1, 1], [1, 0, 1, 1], [1, 1, 0, 1], [1, 1, 1, 0]])
G = nx.Graph(W2)
nx.draw(G)
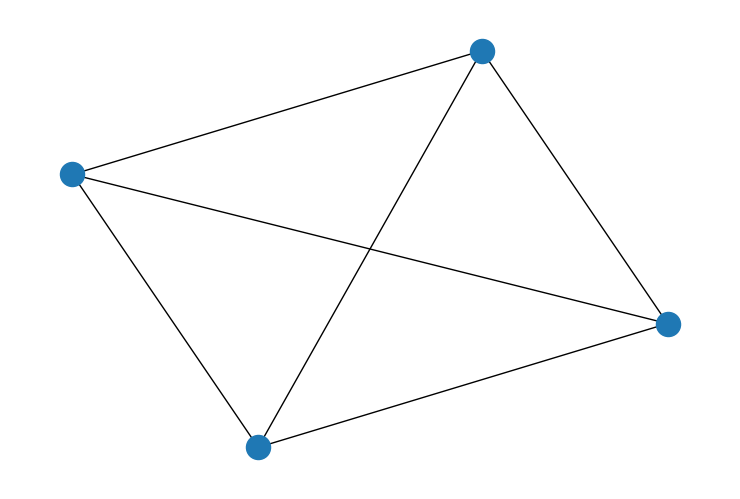
如果节点之间存在强烈的空间协方差,我们应该预期第一个图表比第二个图表允许更多的方差。在第二个图表中,每个节点都对其他所有节点施加影响。因此,最终的结果应该是相对均匀的。
缩放因子是衡量特定邻接矩阵所隐含的方差程度的指标。如果我们为上述两个矩阵计算缩放因子,它证实了我们的直觉。第一个图比第二个图允许更多的方差。
scaling_factor_sp(W1), scaling_factor_sp(W2)
(0.31249999534338707, 0.18749999767169354)
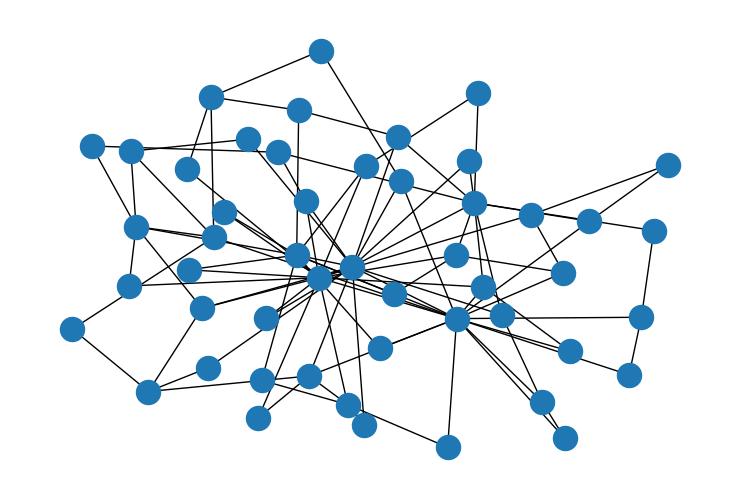
第二个例子可以真正强调这一点。这是两个优先连接图 - 少数节点有很多边,而大多数节点只有很少的边。唯一的区别是最小边数。在第一个图中,每个节点至少有两条边。在第二个图中,每个节点至少有一条边。
G = nx.barabasi_albert_graph(50, 2)
nx.draw(G)
W_sparse = nx.adjacency_matrix(G, dtype="int")
W = W_sparse.toarray()
print("scaling factor: " + str(scaling_factor_sp(W)))
scaling factor: 0.41031348581585425
G = nx.barabasi_albert_graph(50, 1)
nx.draw(G)
W_sparse = nx.adjacency_matrix(G, dtype="int")
W = W_sparse.toarray()
print("scaling factor: " + str(scaling_factor_sp(W)))
scaling factor: 1.7744552306768082
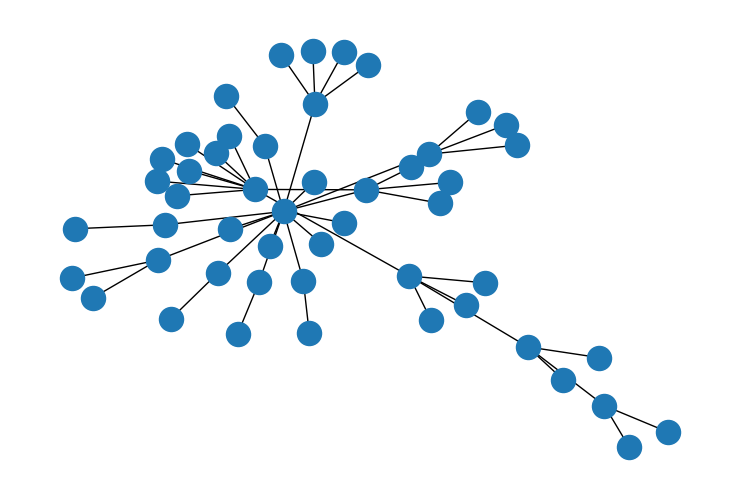
第二个图的缩放因子要高得多,因为它连接得不太均匀。形成具有独特特征的小区域的机会更多。在第一个图中,连接的规律性减少了这种机会。同样,缩放因子证实了我们的直觉。
这澄清了缩放因子所衡量的内容。但我们为什么需要使用它呢?让我们重新审视BYM组件的数学描述:
BYM模型的目标是我们将两种不同类型的随机效应混合在一起,然后\(\sigma\)提供了混合的整体方差。这意味着我们需要非常小心每个随机效应的个体方差——它们都需要大约等于1。确保\(\theta \approx 1\)的方差很容易。我们可以将其作为先验的一部分来指定。获得\(\phi \approx 1\)的方差更难,因为方差来自数据(空间结构),而不是先验。
缩放因子是确保\(\phi\)的方差大致等于1的技巧。当由空间结构隐含的方差非常小,比如说,小于1时,将\(\rho\)除以缩放因子将得到一个大于1的数。换句话说,我们将\(\phi\)的方差扩大,直到它等于1。现在所有其他参数都将正常表现。\(\rho\)表示两个相似事物之间的混合,而\(\sigma\)表示随机效应的联合方差。
理解缩放因子的目的的最后一种方法是想象如果我们不包含它会发生什么。假设图表暗示了非常大的方差,比如上面的第一个优先连接图。在这种情况下,混合参数\(\rho\)可能会拉入更多的\(\phi\),因为数据具有很大的方差,而模型正在寻找任何可以找到的方差来解释它。但这使得结果的解释变得困难。\(\rho\)是否倾向于\(\phi\)是因为实际上存在强烈的空间结构?还是因为它比\(\theta\)具有更高的方差?除非我们重新缩放\(\phi\),否则我们无法分辨。
作者#
由Daniel Saunders于2023年8月撰写(pymc-examples#566)。
参考资料#
安德烈亚·里布勒、西格伦·H·索尔比、丹尼尔·辛普森和哈瓦德·鲁。一种直观的贝叶斯空间模型,用于疾病制图,考虑了缩放因素。医学研究中的统计方法,25(4):1145–1165, 2016。
Mitzi Morris, Katherine Wheeler-Martin, Dan Simpson, Stephen J. Mooney, Andrew Gelman, 和 Charles DiMaggio. 贝叶斯分层空间模型:在Stan中实现Besag York Mollié模型。空间和时空流行病学,31:100301, 2019. URL: https://www.sciencedirect.com/science/article/pii/S1877584518301175, doi:https://doi.org/10.1016/j.sste.2019.100301.
水印#
%load_ext watermark
%watermark -n -u -v -iv -w -p xarray
Last updated: Thu Aug 01 2024
Python implementation: CPython
Python version : 3.11.0
IPython version : 8.8.0
xarray: 2024.3.0
matplotlib: 3.6.2
pytensor : 2.14.2
networkx : 3.0
nutpie : 0.13.0
numpy : 1.24.3
pymc : 5.16.0
pandas : 2.2.2
scipy : 1.10.0
arviz : 0.17.1
Watermark: 2.3.1