贝叶斯因子与边际似然#

import arviz as az
import numpy as np
import pymc as pm

from matplotlib import pyplot as plt
from matplotlib.ticker import FormatStrFormatter
from scipy.special import betaln
from scipy.stats import beta

print(f"Running on PyMC v{pm.__version__}")

Running on PyMC v5.0.0

az.style.use("arviz-darkgrid")

比较模型的“贝叶斯方法”是计算每个模型的边际似然 \(p(y \mid M_k)\)，即给定模型\(M_k\)时观测数据\(y\)的概率。这个量，边际似然，只是贝叶斯定理的归一化常数。如果我们写出贝叶斯定理并明确所有推断都是模型依赖的，我们就可以看到这一点。

\[p (\theta \mid y, M_k ) = \frac{p(y \mid \theta, M_k) p(\theta \mid M_k)}{p( y \mid M_k)}\]

其中：

  • \(y\) 是数据

  • \(\theta\) 参数

  • \(M_k\) K个竞争模型中的一个模型

通常在进行推理时，我们不需要计算这个归一化常数，所以在实际操作中，我们通常计算后验概率到一个常数因子，即：

\[p (\theta \mid y, M_k ) \propto p(y \mid \theta, M_k) p(\theta \mid M_k)\]

然而，对于模型比较和模型平均，边际似然是一个重要的量。虽然这不是执行这些任务的唯一方法，你可以在这里、那里和其他地方阅读关于使用替代方法进行模型平均和模型选择的内容。实际上，与使用边际似然相比，这些替代方法通常是更好的选择。

贝叶斯模型选择#

如果我们的主要目标是仅从一组模型中选择一个最佳模型，我们可以选择具有最大\(p(y \mid M_k)\)的模型。如果所有模型被假设具有相同的先验概率，这是完全合理的。否则，我们必须考虑到并非所有模型都具有相同的先验概率，并计算：

\[p(M_k \mid y) \propto p(y \mid M_k) p(M_k)\]

有时主要目标不仅仅是保留一个模型，而是比较模型以确定哪些模型更有可能以及可能性有多大。这可以通过使用贝叶斯因子来实现：

\[BF_{01} = \frac{p(y \mid M_0)}{p(y \mid M_1)}\]

即两个模型的边际似然比。BF越大，分子中的模型（在本例中为\(M_0\)）就越好。为了便于解释BF，哈罗德·杰弗里斯提出了一种用于解释贝叶斯因子的尺度，具有不同程度的支持或强度。这只是一种将数字转化为文字的方式。

  • 1-3: 轶事

  • 3-10: 中等

  • 10-30: 强

  • 30-100: 非常强

  • \(>\) 100: 极端

请注意，如果你得到的数值小于1，那么支持的是分母中的模型，这些情况下的表格也可用。当然，你也可以直接取上表中数值的倒数，或者取BF值的倒数，这样也是可以的。

记住这些规则非常重要，它们只是约定俗成的简单指南。结果应始终置于我们问题的背景下，并应伴随足够的细节，以便他人可以自行评估是否同意我们的结论。在粒子物理学、法庭或为防止数百人死亡而疏散城镇的情况下，提出主张所需的证据是不同的。

贝叶斯模型平均#

与其从一组候选模型中选择一个单一模型，模型平均是通过对候选模型进行平均来获得一个元模型。贝叶斯版本的这种方法通过每个模型的边际后验概率来加权每个模型。

\[p(\theta \mid y) = \sum_{k=1}^K p(\theta \mid y, M_k) \; p(M_k \mid y)\]

如果先验是正确的，并且正确的模型是我们集合中的一个模型\(M_k\)，那么这是平均模型的最佳方法。否则，贝叶斯模型平均将渐近地选择在比较模型集合中与Kullback-Leibler 散度最接近的单一模型。

查看这个示例作为执行模型平均的替代方法。

一些备注#

现在我们将简要讨论一些关于边际似然的关键事实

  • 好的

    • 奥卡姆剃刀原则包含在内：具有更多参数的模型比具有较少参数的模型受到更大的惩罚。直观的理由是，参数数量越多，先验相对于似然的分散程度就越大。

  • 不好的

    • 计算边际似然通常是一个困难的任务，因为它是在高维参数空间上对一个高度变化的函数进行积分。一般来说，这个积分需要使用或多或少复杂的方法进行数值求解。

\[p(y \mid M_k) = \int_{\theta_k} p(y \mid \theta_k, M_k) \; p(\theta_k | M_k) \; d\theta_k\]

  • 丑陋的

    • 边际似然对每个模型中参数的指定先验敏感依赖于\(p(\theta_k \mid M_k)\)。

请注意，好的和丑陋的是相关的。使用边际似然来比较模型是一个好主意，因为复杂模型的惩罚已经包含在内（从而防止我们过拟合），同时，先验的变化将影响边际似然的计算。起初这听起来有点傻；我们已经知道先验会影响计算（否则我们可以简单地避免它们），但这里的关键词是敏感地。我们讨论的是先验的变化，这些变化将使\(\theta\)的推断或多或少保持不变，但可能会对边际似然的值产生重大影响。

计算贝叶斯因子#

边际似然通常在封闭形式下不可用，除非对于某些受限模型。为此，已经设计了许多方法来计算边际似然及其导出的贝叶斯因子，其中一些方法非常简单且幼稚，在实践中效果非常差。大多数有用的方法最初是在统计力学领域提出的。这种联系之所以被解释，是因为边际似然类似于统计物理学中的一个中心量，称为配分函数，而配分函数又与另一个非常重要的量自由能密切相关。统计力学与贝叶斯推断之间的许多联系总结在这里。

使用层次模型#

贝叶斯因子的计算可以被框架为一个层次模型，其中高层参数是一个分配给每个模型的索引，并从分类分布中采样。换句话说，我们同时对两个（或更多）竞争模型进行推断，并使用一个离散的虚拟变量在模型之间跳转。我们在每个模型上花费的采样时间与\(p(M_k \mid y)\)成正比。

通过这种方式计算贝叶斯因子时，一些常见的问题是，如果一个模型比另一个模型更好，根据定义，我们将花费更多时间从该模型中采样，而不是从另一个模型中采样。这可能导致不准确性，因为我们将会对不太可能的模型进行欠采样。另一个问题是，即使参数不用于拟合该模型，参数的值也会更新。也就是说，当选择模型0时，模型1中的参数会更新，但由于它们不用于解释数据，它们只会受到先验的限制。如果先验过于模糊，当我们选择模型1时，参数值可能与之前接受的值相差太远，因此步骤会被拒绝。因此，我们最终会遇到采样问题。

如果我们发现这些问题，我们可以尝试通过在我们的模型中实施两种修改来改进采样：

  • 理想情况下，如果我们能够平等地访问这两个模型，我们就可以获得更好的采样，因此我们可以调整每个模型的先验，以支持不太有利的模型，而不利于最有利的模型。这不会影响贝叶斯因子的计算，因为我们必须在计算中包含先验。

  • 使用伪先验，正如Kruschke等人所建议的那样。这个想法很简单：如果问题是当模型未被选中时，参数会不受限制地漂移，那么一个解决方案是尝试在不被使用时人为地限制它们！你可以在Kruschke的书中找到一个使用伪先验的模型示例，并且该模型已被移植到Python/PyMC3。

如果你想了解更多关于这种边际似然计算方法的内容，请参阅《Doing Bayesian Data Analysis》第12章。本章还讨论了如何使用贝叶斯因子作为经典假设检验的贝叶斯替代方法。

分析性地#

对于某些模型，例如beta-二项式模型（又称抛硬币模型），我们可以解析地计算边际似然。如果我们将这个模型写为：

\[\theta \sim Beta(\alpha, \beta)\]
\[y \sim Bin(n=1, p=\theta)\]

边缘似然（marginal likelihood）将是：

\[p(y) = \binom {n}{h} \frac{B(\alpha + h,\ \beta + n - h)} {B(\alpha, \beta)}\]

其中：

  • \(B\) 是 beta 函数，不要与 \(Beta\) 分布混淆

  • \(n\) 是试验的次数

  • \(h\) 是成功的次数

由于我们只关心在两个不同模型下（对于相同数据）边际似然的相对值，我们可以省略二项式系数 \(\binom {n}{h}\)，因此我们可以写成：

\[p(y) \propto \frac{B(\alpha + h,\ \beta + n - h)} {B(\alpha, \beta)}\]

这个表达式已经在下面的单元格中编码，但有一个变化。我们将使用betaln函数而不是beta函数，这样做是为了防止下溢。

def beta_binom(prior, y):
    """
    Compute the marginal likelihood, analytically, for a beta-binomial model.

    prior : tuple
        tuple of alpha and beta parameter for the prior (beta distribution)
    y : array
        array with "1" and "0" corresponding to the success and fails respectively
    """
    alpha, beta = prior
    h = np.sum(y)
    n = len(y)
    p_y = np.exp(betaln(alpha + h, beta + n - h) - betaln(alpha, beta))
    return p_y

我们用于此示例的数据包括100次“抛硬币”的结果，观察到的“正面”和“反面”数量相同。我们将比较两个模型，一个使用均匀先验，另一个使用围绕\(\theta = 0.5\)的更集中的先验。

y = np.repeat([1, 0], [50, 50])  # 50 "heads" and 50 "tails"
priors = ((1, 1), (30, 30))

for a, b in priors:
    distri = beta(a, b)
    x = np.linspace(0, 1, 300)
    x_pdf = distri.pdf(x)
    plt.plot(x, x_pdf, label=rf"$\alpha$ = {a:d}, $\beta$ = {b:d}")
    plt.yticks([])
    plt.xlabel("$\\theta$")
    plt.legend()
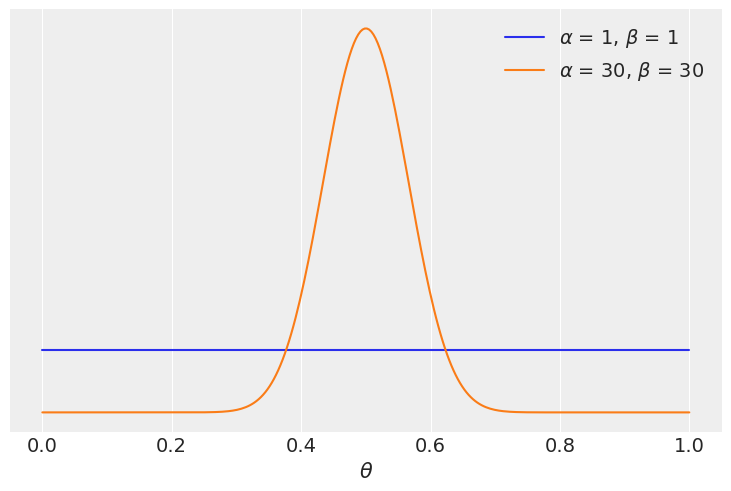
../_images/9ee9964c2412dbdb8b9c1fd52eed3de489c26d3171c3a95e08dbf033fd4e0e6e.png

以下单元格返回贝叶斯因子

BF = beta_binom(priors[1], y) / beta_binom(priors[0], y)
print(round(BF))

5

我们看到，具有更集中先验分布的模型 \(\text{beta}(30, 30)\) 的支持度比具有更广泛先验分布的模型 \(\text{beta}(1, 1)\) 高出大约5倍。除了确切的数值之外，这并不令人惊讶，因为最受青睐模型的先验分布集中在 \(\theta = 0.5\) 附近，而数据 \(y\) 具有相同数量的正面和反面，这与 \(\theta\) 值在0.5左右一致。

顺序蒙特卡罗#

The 顺序蒙特卡罗 采样器是一种通过一系列从先验到后验的连续退火序列来推进的方法。这个过程的一个很好的副产品是我们得到了边际似然度的估计。实际上，由于数值原因，返回的值是对数边际似然度（这有助于避免下溢）。

models = []
idatas = []
for alpha, beta in priors:
    with pm.Model() as model:
        a = pm.Beta("a", alpha, beta)
        yl = pm.Bernoulli("yl", a, observed=y)
        idata = pm.sample_smc(random_seed=42)
        models.append(model)
        idatas.append(idata)

Initializing SMC sampler...
Sampling 4 chains in 4 jobs
100.00% [100/100 00:00<? Stage: 2 Beta: 1.000] 
    

/home/oriol/bin/miniconda3/envs/releases/lib/python3.10/site-packages/arviz/data/base.py:221: UserWarning: More chains (4) than draws (3). Passed array should have shape (chains, draws, *shape)
  warnings.warn(
Initializing SMC sampler...
Sampling 4 chains in 4 jobs
100.00% [100/100 00:00<? Stage: 0 Beta: 1.000] 
    

/home/oriol/bin/miniconda3/envs/releases/lib/python3.10/site-packages/arviz/data/base.py:221: UserWarning: More chains (4) than draws (1). Passed array should have shape (chains, draws, *shape)
  warnings.warn(

BF_smc = np.exp(
    idatas[1].sample_stats["log_marginal_likelihood"].mean()
    - idatas[0].sample_stats["log_marginal_likelihood"].mean()
)
np.round(BF_smc).item()

5.0

正如我们从上一个单元格中看到的，SMC给出的答案与解析计算的结果基本相同！

注意：在上面的单元格中我们计算了一个差值（而不是除法），因为我们是在对数尺度上，出于同样的原因，我们在返回结果之前取了指数。最后，我们计算均值的原因是因为我们为每个链获得了一个对数边际似然值。

使用SMC计算（对数）边际似然的优势在于，我们可以在更广泛的模型范围内使用它，因为不再需要闭式表达式。我们为这种灵活性付出的代价是计算成本更高。请注意，SMC（使用PyMC中实现的独立Metropolis核）不像基于梯度的采样器（如NUTS）那样高效或稳健。随着问题维度的增加，更准确地估计后验和边际似然将需要更多的抽取，秩图可以帮助诊断SMC的采样问题。

贝叶斯因子与推断#

到目前为止，我们使用了贝叶斯因子来判断哪个模型似乎更能解释数据，并且我们得出其中一个模型比另一个模型\(\approx 5\) 更好。

但是这些模型得到的后验分布如何？它们有多么不同？

az.summary(idatas[0], var_names="a", kind="stats").round(2)
mean sd hdi_3% hdi_97%
a 0.5 0.05 0.4 0.59 
az.summary(idatas[1], var_names="a", kind="stats").round(2)
mean sd hdi_3% hdi_97%
a 0.5 0.04 0.42 0.57

我们可以说结果非常相似，我们对\(\theta\)有相同的均值，并且model_0的后验分布略宽，正如预期的那样，因为这个模型的先验分布更宽。我们还可以检查后验预测分布，看看它们有多相似。

ppc_0 = pm.sample_posterior_predictive(idatas[0], model=models[0]).posterior_predictive
ppc_1 = pm.sample_posterior_predictive(idatas[1], model=models[1]).posterior_predictive

Sampling: [yl]
100.00% [8000/8000 00:00<00:00] 
Sampling: [yl]
100.00% [8000/8000 00:00<00:00] 
_, ax = plt.subplots(figsize=(9, 6))

bins = np.linspace(0.2, 0.8, 8)
ax = az.plot_dist(
    ppc_0["yl"].mean("yl_dim_2"),
    label="model_0",
    kind="hist",
    hist_kwargs={"alpha": 0.5, "bins": bins},
)
ax = az.plot_dist(
    ppc_1["yl"].mean("yl_dim_2"),
    label="model_1",
    color="C1",
    kind="hist",
    hist_kwargs={"alpha": 0.5, "bins": bins},
    ax=ax,
)
ax.legend()
ax.set_xlabel("$\\theta$")
ax.xaxis.set_major_formatter(FormatStrFormatter("%0.1f"))
ax.set_yticks([]);
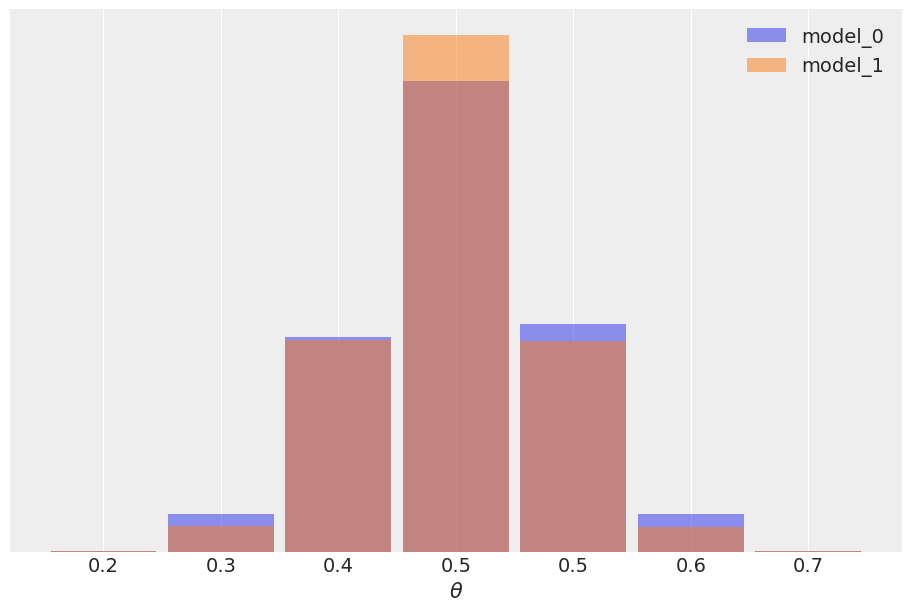
../_images/28828ea3c7b446eb1d7026396feee37e36b3633b38b38aeeec92e05ca1d8243b.png

在这个例子中，观测数据 \(y\) 与 model_1 更一致（因为先验集中在 \(\theta\) 的正确值附近），而不是 model_0（它对 \(\theta\) 的每个可能值赋予相同的概率），这种差异通过贝叶斯因子捕捉到。我们可以说贝叶斯因子在衡量哪个模型作为一个整体更好，包括可能与参数推断无关的先验细节。事实上，在这个例子中，我们还可以看到，即使两个模型具有不同的贝叶斯因子，但仍然可以得到非常相似的预测。原因是数据足够信息丰富，可以减少先验的影响，直到导致非常相似的后验分布。由于预测是从后验计算的，因此我们也得到了非常相似的预测。在大多数比较模型的场景中，我们真正关心的是模型的预测准确性，如果两个模型具有相似的预测准确性，我们认为这两个模型是相似的。为了估计预测准确性，我们可以使用像 PSIS-LOO-CV（az.loo）、WAIC（az.waic）或交叉验证这样的工具。

Savage-Dickey密度比#

对于前面的例子，我们比较了两个beta-二项分布模型，但有时我们想要做的是将一个零假设H_0（或零模型）与一个备择假设H_1进行比较。例如，为了回答问题这枚硬币是否偏向？，我们可以将值\(\theta = 0.5\)（表示没有偏向）与一个允许\(\theta\)变化的模型结果进行比较。在这种比较中，零模型嵌套在备择模型中，这意味着零模型是我们正在构建的模型的特定值。在这种情况下，计算贝叶斯因子非常容易，并且不需要任何特殊方法，因为数学计算很方便，我们只需要在备择模型下比较在零值（例如\(\theta = 0.5\)）处的先验和后验。我们可以从以下表达式中看出这是正确的：

\[ BF_{01} = \frac{p(y \mid H_0)}{p(y \mid H_1)} \frac{p(\theta=0.5 \mid y, H_1)}{p(\theta=0.5 \mid H_1)} \]

仅当 H_0 是 H_1 的特定情况时，成立。

让我们用PyMC和ArviZ来实现。我们只需要获取模型的后验和先验样本。让我们尝试使用之前看到的具有均匀先验的beta-binomial模型。

with pm.Model() as model_uni:
    a = pm.Beta("a", 1, 1)
    yl = pm.Bernoulli("yl", a, observed=y)
    idata_uni = pm.sample(2000, random_seed=42)
    idata_uni.extend(pm.sample_prior_predictive(8000))

Auto-assigning NUTS sampler...
Initializing NUTS using jitter+adapt_diag...
Multiprocess sampling (4 chains in 4 jobs)
NUTS: [a]
100.00% [12000/12000 00:01<00:00 Sampling 4 chains, 0 divergences] 
Sampling 4 chains for 1_000 tune and 2_000 draw iterations (4_000 + 8_000 draws total) took 2 seconds.
Sampling: [a, yl]

现在我们调用 ArviZ 的 az.plot_bf 函数

az.plot_bf(idata_uni, var_name="a", ref_val=0.5);
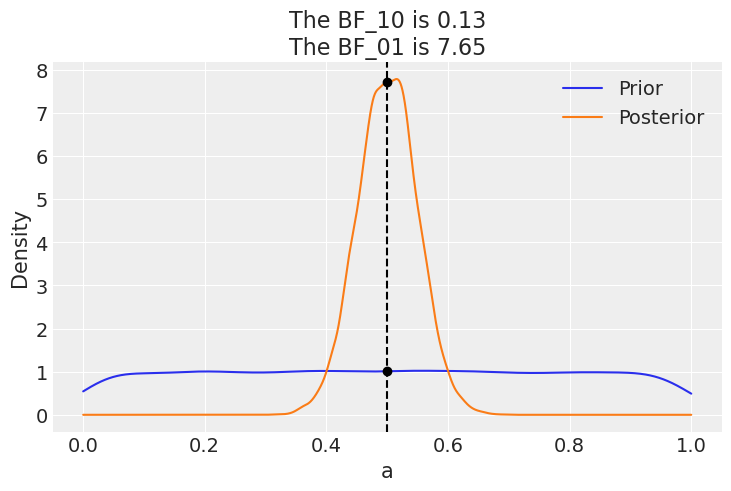
../_images/93c562d90c210b4eee9731f7e3adf06f4c54bf60db206322ea41262dc16c6290.png

该图显示了先验（蓝色）和后验（橙色）的核密度估计（KDE）。两个黑点表示我们在0.5处评估这两个分布。我们可以看到，支持零假设的贝叶斯因子BF_01约为8，这可以解释为支持零假设的中等证据（参见我们之前讨论的杰弗里斯量表）。

正如我们已经讨论过的，贝叶斯因子是衡量哪个模型作为一个整体，能更好地解释数据。这包括先验，即使先验对后验计算的影响相对较小。当我们将第二个模型与空模型进行比较时，我们也可以看到先验的这种影响。

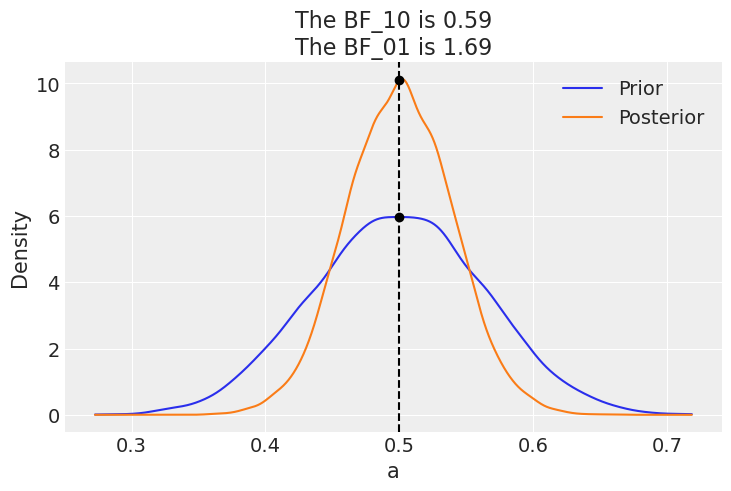
如果我们的模型是一个带有先验beta(30, 30)的beta-二项分布，BF_01会更低（在Jeffreys’尺度上为轶事）。这是因为在这个模型下，\(\theta=0.5\)的先验概率比均匀先验要大得多，因此后验和先验会更加相似。也就是说，在收集数据后，看到后验集中在0.5附近并不令人惊讶。

让我们自己计算一下看看。

with pm.Model() as model_conc:
    a = pm.Beta("a", 30, 30)
    yl = pm.Bernoulli("yl", a, observed=y)
    idata_conc = pm.sample(2000, random_seed=42)
    idata_conc.extend(pm.sample_prior_predictive(8000))

Auto-assigning NUTS sampler...
Initializing NUTS using jitter+adapt_diag...
Multiprocess sampling (4 chains in 4 jobs)
NUTS: [a]
100.00% [12000/12000 00:01<00:00 Sampling 4 chains, 0 divergences] 
Sampling 4 chains for 1_000 tune and 2_000 draw iterations (4_000 + 8_000 draws total) took 2 seconds.
Sampling: [a, yl]

az.plot_bf(idata_conc, var_name="a", ref_val=0.5);
../_images/06970480642adff8bd4365ae81ca639f02eb7316cbeb1ad27dba75a3046a7fb1.png

  • 由Osvaldo Martin于2017年9月撰写（pymc#2563）

  • 由Osvaldo Martin于2018年8月更新（pymc#3124）

  • 由Osvaldo Martin于2022年5月更新（pymc-examples#342）

  • 由Osvaldo Martin于2022年11月更新

  • 由Reshama Shaikh在2023年1月使用PyMC v5重新执行

参考资料#

[1]

詹姆斯·M. 迪基和B. P. 利恩茨。加权似然比，关于机会的尖锐假设，马尔可夫链的阶数。数理统计年鉴，41(1):214 – 226，1970年。doi:10.1214/aoms/1177697203。

[2]

埃里克-扬·瓦格纳克斯、汤姆·洛德维克斯、希曼舒·库里亚尔和拉乌尔·格拉斯曼。心理学家贝叶斯假设检验：关于萨维奇-迪克西方法的教程。认知心理学，60(3):158–189，2010年。URL: https://www.sciencedirect.com/science/article/pii/S0010028509000826，doi:https://doi.org/10.1016/j.cogpsych.2009.12.001。

水印#

%load_ext watermark
%watermark -n -u -v -iv -w -p pytensor

Last updated: Sun Jan 15 2023

Python implementation: CPython
Python version       : 3.10.8
IPython version      : 8.7.0

pytensor: 2.8.10

matplotlib: 3.6.2
numpy     : 1.24.0
pymc      : 5.0.0
arviz     : 0.14.0

Watermark: 2.3.1

许可证声明#

本示例库中的所有笔记本均在MIT许可证下提供，该许可证允许修改和重新分发，前提是保留版权和许可证声明。

引用 PyMC 示例#

要引用此笔记本，请使用Zenodo为pymc-examples仓库提供的DOI。

重要

许多笔记本是从其他来源改编的：博客、书籍……在这种情况下，您应该引用原始来源。

同时记得引用代码中使用的相关库。

这是一个BibTeX的引用模板：

@incollection{citekey,
  author    = "<notebook authors, see above>",
  title     = "<notebook title>",
  editor    = "PyMC Team",
  booktitle = "PyMC examples",
  doi       = "10.5281/zenodo.5654871"
}

渲染后可能看起来像：