模型平均#

import os

import arviz as az
import matplotlib.pyplot as plt
import numpy as np
import pandas as pd
import pymc as pm

print(f"Running on PyMC v{pm.__version__}")

Running on PyMC v5.16.2+24.g799c98f41

rng = np.random.seed(2741)
az.style.use("arviz-darkgrid")

当面对多个模型时，我们有几种选择。其中之一是进行模型选择，如PyMC示例模型比较和GLM: 模型选择所示，通常在决定保留哪个模型时，进行后验预测检查是一个好主意。丢弃所有模型只保留一个模型相当于断言，在评估的模型中，有一个模型是正确的（在某些标准下），概率为1，其余的都是不正确的。在大多数情况下，这将是一种过度陈述，忽略了我们对模型的不确定性。这有点类似于计算完整的后验分布，然后只保留一个点估计，比如后验均值；我们可能会变得过于自信，认为自己真正了解的东西。您还可以浏览blog/tag/model-comparison标签以查找相关帖子。

解决这个困境的另一种方法是进行模型选择，但同时承认我们丢弃的模型。如果模型的数量不是很大，这可以成为论文、演示、论文等技术讨论的一部分。如果听众不够技术，这可能不是一个好主意。

另一个替代方案，即本例的主题，是执行模型平均。其思想是根据每个模型的优点对其进行加权，并根据这些权重从每个模型生成预测。有几种方法可以做到这一点，包括将在本笔记本中简要讨论的三种方法。您将在Yao et al. [2018] 和 Yao et al. [2022] 的工作中找到更详尽的解释。

伪贝叶斯模型平均#

贝叶斯模型可以通过其边际似然进行加权，这被称为贝叶斯模型平均。虽然这在理论上很有吸引力，但在实践中存在问题：一方面，边际似然对先验的设定高度敏感，而参数估计则不然，另一方面，计算边际似然通常是一个具有挑战性的任务。此外，在\(\mathcal{M}\)-开放设置中，贝叶斯模型平均存在缺陷，其中真实的数据生成过程不是所拟合的候选模型之一Yao et al. [2018]。一种更稳健的方法是计算期望对数点预测密度（ELPD）。

\[ \sum_i^N \log \int \ p(y_i \mid \theta) \; p(\theta \mid y) d\theta \]

其中 \(N\) 是数据点的数量，\(y_i\) 是第 i 个数据点，\(\theta\) 是模型的参数，\(p(y_i \mid \theta)\) 是给定参数的第 i 个数据点的似然性，\(p(\theta \mid y)\) 是后验分布。

一旦我们为每个模型计算了ELPD，我们就可以通过以下方式计算权重

\[w_i = \frac {e^{dELPD_i}} {\sum_j^M e^{dELPD_i}}\]

其中 \(dELPD_i\) 是具有最佳ELPD的模型与第i个模型之间的差异。

这种方法称为伪贝叶斯模型平均，或类似Akaike的加权，是一种启发式方法，用于计算每个模型（给定一组固定模型）的相对概率。请注意，我们对ELPD公式中的对数效应进行指数化以“还原”其效果，分母是一个归一化项，以确保权重总和为1。带着一丝谨慎，我们可以将这些权重解释为每个模型解释数据的概率。

到目前为止一切顺利，但ELPD是一个理论量，在实践中我们需要对其进行近似。为此，ArviZ提供了两种方法

  • WAIC，广泛适用信息准则

  • LOO, 帕累托平滑留一交叉验证。

两者都需要带有对数似然组的数据，并且在计算速度上同样快。我们推荐使用LOO，因为它具有更好的实际特性，并且有更好的诊断功能（因此我们可以知道何时在对ELPD估计时遇到问题）。

伪贝叶斯模型平均与贝叶斯自助法#

上述计算权重的公式是一个不错且简单的方法，但有一个主要缺点：它没有考虑到ELPD计算中的不确定性。我们可以计算ELPD值的标准误差（假设为高斯近似），并相应地修改上述公式。或者我们可以做一些更稳健的事情，比如使用贝叶斯自助法来估计并纳入这种不确定性。

堆叠#

我们将讨论的第三种方法是通过Yao 等人 [2018]提出的预测分布堆叠。我们希望在一个元模型中组合多个模型，以最小化元模型与真实生成模型之间的差异。当使用对数评分规则时，这相当于：

\[\max_{w} \frac{1}{n} \sum_{i=1}^{n}log\sum_{k=1}^{K} w_k p(y_i \mid y_{-i}, M_k)\]

其中 \(n\) 是数据点的数量，\(K\) 是模型的数量。为了强制得到一个解，我们约束 \(w\) 为 \(w_k \ge 0\) 并且 \(\sum_{k=1}^{K} w_k = 1\)。

数量 \(p(y_i \mid y_{-i}, M_k)\) 是 \(M_k\) 模型的留一法预测分布。计算它需要将每个模型 \(n\) 次，每次留下一个数据点。幸运的是，这正是 LOO 以非常高效的方式近似的内容。因此，我们可以将 LOO 和 stacking 结合使用。公平地说，我们也可以使用 WAIC，即使 WAIC 以不同的方式近似 ELPD。

加权后验预测样本#

一旦我们使用上述三种方法中的任何一种计算出权重，我们就可以使用它们来获取加权后验预测样本。我们将使用体脂数据集来说明如何进行此操作 [Penrose 等人，1985]。该数据集包含251个个体的测量数据，包括他们的体重、身高、腹围、腕围等。我们的目的是预测体脂百分比，由siri变量估计，该变量也可从数据集中获得。

让我们从加载数据开始

try:
    d = pd.read_csv(os.path.join("..", "data", "body_fat.csv"))
except FileNotFoundError:
    d = pd.read_csv(pm.get_data("body_fat.csv"))

d.head()
siri age weight height neck chest abdomen hip thigh knee ankle biceps forearm wrist
0 12.3 23 70.1 172 36.2 93.1 85.2 94.5 59.0 37.3 21.9 32.0 27.4 17.1
1 6.1 22 78.8 184 38.5 93.6 83.0 98.7 58.7 37.3 23.4 30.5 28.9 18.2
2 25.3 22 70.0 168 34.0 95.8 87.9 99.2 59.6 38.9 24.0 28.8 25.2 16.6
3 10.4 26 84.0 184 37.4 101.8 86.4 101.2 60.1 37.3 22.8 32.4 29.4 18.2
4 28.7 24 83.8 181 34.4 97.3 100.0 101.9 63.2 42.2 24.0 32.2 27.7 17.7

现在我们已经有了数据，我们将构建两个模型，这两个模型都是简单的线性回归，不同之处在于对于第一个模型，我们将使用变量abdomen，而对于第二个模型，我们将使用变量wrist、height和weight。

with pm.Model() as model_0:
    alpha = pm.Normal("alpha", mu=0, sigma=1)
    beta = pm.Normal("beta", mu=0, sigma=1)
    sigma = pm.HalfNormal("sigma", 5)

    mu = alpha + beta * d["abdomen"]

    siri = pm.Normal("siri", mu=mu, sigma=sigma, observed=d["siri"])

    idata_0 = pm.sample(idata_kwargs={"log_likelihood": True}, random_seed=rng)
    pm.sample_posterior_predictive(idata_0, extend_inferencedata=True, random_seed=rng)

Auto-assigning NUTS sampler...
Initializing NUTS using jitter+adapt_diag...
Multiprocess sampling (4 chains in 4 jobs)
NUTS: [alpha, beta, sigma]





Sampling 4 chains for 1_000 tune and 1_000 draw iterations (4_000 + 4_000 draws total) took 7 seconds.
Sampling: [siri]

















with pm.Model() as model_1:
    alpha = pm.Normal("alpha", mu=0, sigma=1)
    beta = pm.Normal("beta", mu=0, sigma=1, shape=3)
    sigma = pm.HalfNormal("sigma", 5)

    mu = alpha + pm.math.dot(beta, d[["wrist", "height", "weight"]].T)

    siri = pm.Normal("siri", mu=mu, sigma=sigma, observed=d["siri"])

    idata_1 = pm.sample(idata_kwargs={"log_likelihood": True}, random_seed=rng)
    pm.sample_posterior_predictive(idata_1, extend_inferencedata=True, random_seed=rng)









Auto-assigning NUTS sampler...
Initializing NUTS using jitter+adapt_diag...
Multiprocess sampling (4 chains in 4 jobs)
NUTS: [alpha, beta, sigma]









Sampling 4 chains for 1_000 tune and 1_000 draw iterations (4_000 + 4_000 draws total) took 36 seconds.
Sampling: [siri]













在使用LOO（或WAIC）比较或平均模型之前，我们应该检查是否存在采样问题，并且后验预测检查是合理的。为了简洁起见，我们将跳过这些步骤，直接进入模型平均。


首先，我们需要调用 az.compare 来计算每个模型的 LOO 值和使用 stacking 的权重。这些是默认选项，如果你想执行伪贝叶斯模型平均，你可以使用 method='BB-pseudo-BMA'，其中包括贝叶斯引导估计 ELPD 的不确定性。






model_dict = dict(zip(["model_0", "model_1"], [idata_0, idata_1]))
comp = az.compare(model_dict)
comp

















rank
elpd_loo
p_loo
elpd_diff
weight
se
dse
warning
scale






model_1
0
-817.216895
3.626704
0.000000
0.639236
10.496342
0.000000
False
log




model_0
1
-825.344978
1.832909
8.128083
0.360764
9.970768
8.698358
False
log










我们可以从weight列中看到，model_1的权重为\(\approx 0.6\)，而model_2的权重为\(\approx 0.4\)。要使用这些权重生成后验预测样本，我们可以使用az.weighted_posterior函数。该函数接受InferenceData对象和权重，并返回一个新的InferenceData对象。






ppc_w = az.weight_predictions(
    [model_dict[name] for name in comp.index],
    weights=comp.weight,
)
ppc_w















arviz.InferenceData




    

  • 



    

    

      

      















      <xarray.Dataset>
Dimensions:     (siri_dim_2: 251, sample: 3999)
Coordinates:
  * siri_dim_2  (siri_dim_2) int64 0 1 2 3 4 5 6 ... 244 245 246 247 248 249 250
  * sample      (sample) object MultiIndex
  * chain       (sample) int64 2 3 1 2 1 2 3 3 3 3 3 3 ... 3 3 3 1 0 0 2 0 2 1 2
  * draw        (sample) int64 682 691 550 397 831 520 ... 638 997 295 483 606 9
Data variables:
    siri        (siri_dim_2, sample) float64 17.75 16.43 14.7 ... 30.98 27.67
Attributes:
    created_at:                 2024-08-23T16:10:41.836182+00:00
    arviz_version:              0.20.0.dev0
    inference_library:          pymc
    inference_library_version:  5.16.2+24.g799c98f41

      

    

    

    • 

  • 



    

    

      

      















      <xarray.Dataset>
Dimensions:     (siri_dim_0: 251)
Coordinates:
  * siri_dim_0  (siri_dim_0) int64 0 1 2 3 4 5 6 ... 244 245 246 247 248 249 250
Data variables:
    siri        (siri_dim_0) float64 12.3 6.1 25.3 10.4 ... 33.6 29.3 26.0 31.9
Attributes:
    created_at:                 2024-08-23T16:10:41.440917+00:00
    arviz_version:              0.20.0.dev0
    inference_library:          pymc
    inference_library_version:  5.16.2+24.g799c98f41

      

    

    

    • 









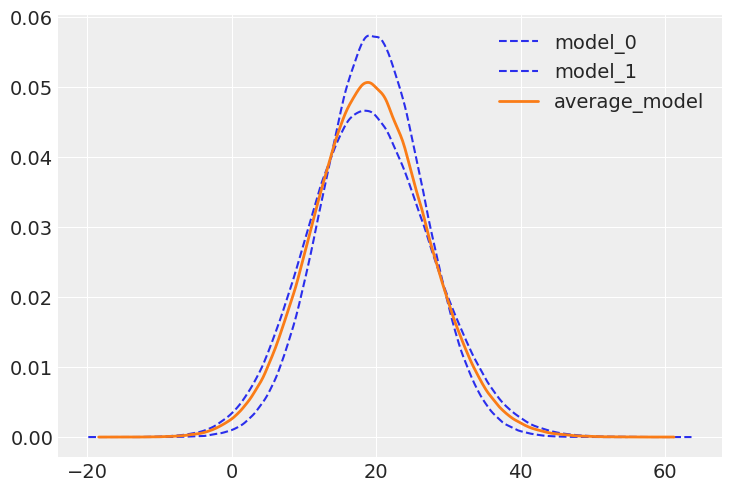
从下面的图中我们可以看到，平均模型是两个模型的组合。






az.plot_kde(
    idata_0.posterior_predictive["siri"].values,
    plot_kwargs={"color": "C0", "linestyle": "--"},
    label="model_0",
)
az.plot_kde(
    idata_1.posterior_predictive["siri"].values,
    plot_kwargs={"color": "C0", "linestyle": "--"},
    label="model_1",
)
az.plot_kde(
    ppc_w.posterior_predictive["siri"].values,
    plot_kwargs={"color": "C1", "linewidth": 2},
    label="average_model",
);








../_images/04dfc13dad24652049eae900d067708b33c326a1cc0a809d54446806b8c88fe5.png









做还是不做？#


模型平均是一个好主意，当你想要提高预测的稳健性时。通常，模型的组合会比任何单一模型具有更好的预测性能。当模型互补时，这一点尤其正确。在这个例子中我们没有探讨的是，为模型分配权重，使得它们在数据的不同部分有所变化。正如Yao et al. [2022]所讨论的那样，这是可以做到的。


什么时候不适合进行模型平均？很多时候我们可以创建新的模型，这些模型有效地作为其他模型的平均值。例如，在这个例子中，我们可以创建一个包含所有变量的新模型。这实际上是一个非常明智的做法。请注意，如果一个模型排除了某个变量，这相当于将该变量的系数设置为零。如果我们对包含该变量的模型和不包含该变量的模型进行平均，就像将该变量的系数设置为介于零和包含该变量的模型中的系数值之间的某个值。这是一个非常简单的例子，但同样的推理也适用于更复杂的模型。


分层模型是另一个例子，我们构建一个连续版本的模型，而不是处理离散版本。一个简单的例子是想象我们有一个硬币，我们想要估计它的偏差程度，一个介于0和1之间的数字，具有0.5的等概率出现正面和反面（公平硬币）。我们可以考虑两种独立的模型：一种模型偏向于正面，另一种模型偏向于反面。我们可以分别拟合这两种模型，然后对它们进行平均。另一种方法是构建一个分层模型来估计先验分布。我们不是考虑两种离散模型，而是计算一个连续模型，将离散模型视为特定情况。哪种方法更好？这取决于我们的具体问题。我们是否有充分的理由考虑两种离散模型，还是我们的问题更适合用一个更大的连续模型来表示？






作者#


    

  • 由Osvaldo Martin于2017年6月撰写（pymc#2273）
    • 

  • 由Osvaldo Martin于2017年12月更新（pymc#2741）
    • 

  • 由Marco Gorelli于2020年11月更新（pymc#4271）
    • 

  • 于2020年12月从pymc迁移到pymc-examples仓库（pymc-examples#8）
    • 

  • 由Raul Maldonado于2021年2月更新（pymc#25）
    • 

  • 由 @reshamas 于 2022 年 8 月更新了 Markdown 和样式，(pymc-examples#414)
    • 

  • 更新了笔记本以使用 pymc 5，由 Adrien Porter 于 2023 年 11 月
    • 

  • 由Osvaldo Martin于2024年8月更新
    • 







参考资料#







[1]
(1,2,3)

姚昱玲, Aki Vehtari, Daniel Simpson, 和 Andrew Gelman. 使用堆叠来平均贝叶斯预测分布（含讨论）。贝叶斯分析, 2018年9月。URL: https://doi.org/10.1214\%2F17-ba1091, doi:10.1214/17-ba1091.





[2]
(1,2)

姚昱玲, 格雷戈尔·皮尔斯, 阿基·维塔里, 和安德鲁·格尔曼. 贝叶斯层次堆叠: 有些模型在某些地方是有用的. 贝叶斯分析, 17(4):1043 – 1071, 2022. URL: https://doi.org/10.1214/21-BA1287, doi:10.1214/21-BA1287.





[3]

K. W. Penrose, A. G. Nelson, 和 A. G. Fisher. 使用简单测量技术的男性广义身体成分预测方程。运动医学与科学，17(2):189，1985年4月。URL: https://journals.lww.com/acsm-msse/citation/1985/04000/generalized_body_composition_prediction_equation.37.aspx（访问于2023-10-17）。












水印#






%load_ext watermark
%watermark -n -u -v -iv -w









Last updated: Fri Aug 23 2024

Python implementation: CPython
Python version       : 3.11.5
IPython version      : 8.16.1

arviz     : 0.20.0.dev0
pandas    : 2.1.2
pymc      : 5.16.2+24.g799c98f41
numpy     : 1.24.4
matplotlib: 3.8.4

Watermark: 2.4.3













许可证声明#


本示例库中的所有笔记本均在MIT许可证下提供，该许可证允许修改和重新分发，前提是保留版权和许可证声明。






引用 PyMC 示例#


要引用此笔记本，请使用Zenodo为pymc-examples仓库提供的DOI。




重要


许多笔记本是从其他来源改编的：博客、书籍……在这种情况下，您应该引用原始来源。


同时记得引用代码中使用的相关库。




这是一个BibTeX的引用模板：


@incollection{citekey,
  author    = "<notebook authors, see above>",
  title     = "<notebook title>",
  editor    = "PyMC Team",
  booktitle = "PyMC examples",
  doi       = "10.5281/zenodo.5654871"
}





渲染后可能看起来像：