依赖密度回归#

在另一个示例中，我们展示了如何使用Dirichlet过程进行贝叶斯非参数密度估计。这个示例扩展了前一个示例，说明了依赖密度回归。

正如狄利克雷过程混合模型可以被认为是选择活动组件数量作为推理一部分的无限混合模型，依赖密度回归可以被认为是选择活动专家作为推理一部分的无限专家混合。它们的灵活性和模块化使它们成为执行非参数贝叶斯数据分析的强大工具。

import arviz as az
import numpy as np
import pandas as pd
import pymc3 as pm
import seaborn as sns

from IPython.display import HTML
from matplotlib import animation as ani
from matplotlib import pyplot as plt
from theano import tensor as tt

print(f"Running on PyMC3 v{pm.__version__}")

Running on PyMC3 v3.11.2

%config InlineBackend.figure_format = 'retina'
plt.rc("animation", writer="ffmpeg")
blue, *_ = sns.color_palette()
az.style.use("arviz-darkgrid")
SEED = 972915  # from random.org; for reproducibility
np.random.seed(SEED)

我们将使用Larry Wasserman的优秀书籍《All of Nonparametric Statistics》中的LIDAR数据集。我们对数据集进行了标准化处理，以提高样本的收敛速度。

DATA_URI = "http://www.stat.cmu.edu/~larry/all-of-nonpar/=data/lidar.dat"


def standardize(x):
    return (x - x.mean()) / x.std()


df = pd.read_csv(DATA_URI, sep=r"\s{1,3}", engine="python").assign(
    std_range=lambda df: standardize(df.range), std_logratio=lambda df: standardize(df.logratio)
)

df.head()

	range	logratio	std_range	std_logratio
0	390	-0.050356	-1.717725	0.852467
1	391	-0.060097	-1.707299	0.817981
2	393	-0.041901	-1.686447	0.882398
3	394	-0.050985	-1.676020	0.850240
4	396	-0.059913	-1.655168	0.818631

我们绘制了下面的LIDAR数据。

fig, ax = plt.subplots(figsize=(8, 6))

ax.scatter(df.std_range, df.std_logratio, color=blue)

ax.set_xticklabels([])
ax.set_xlabel("Standardized range")

ax.set_yticklabels([])
ax.set_ylabel("Standardized log ratio");

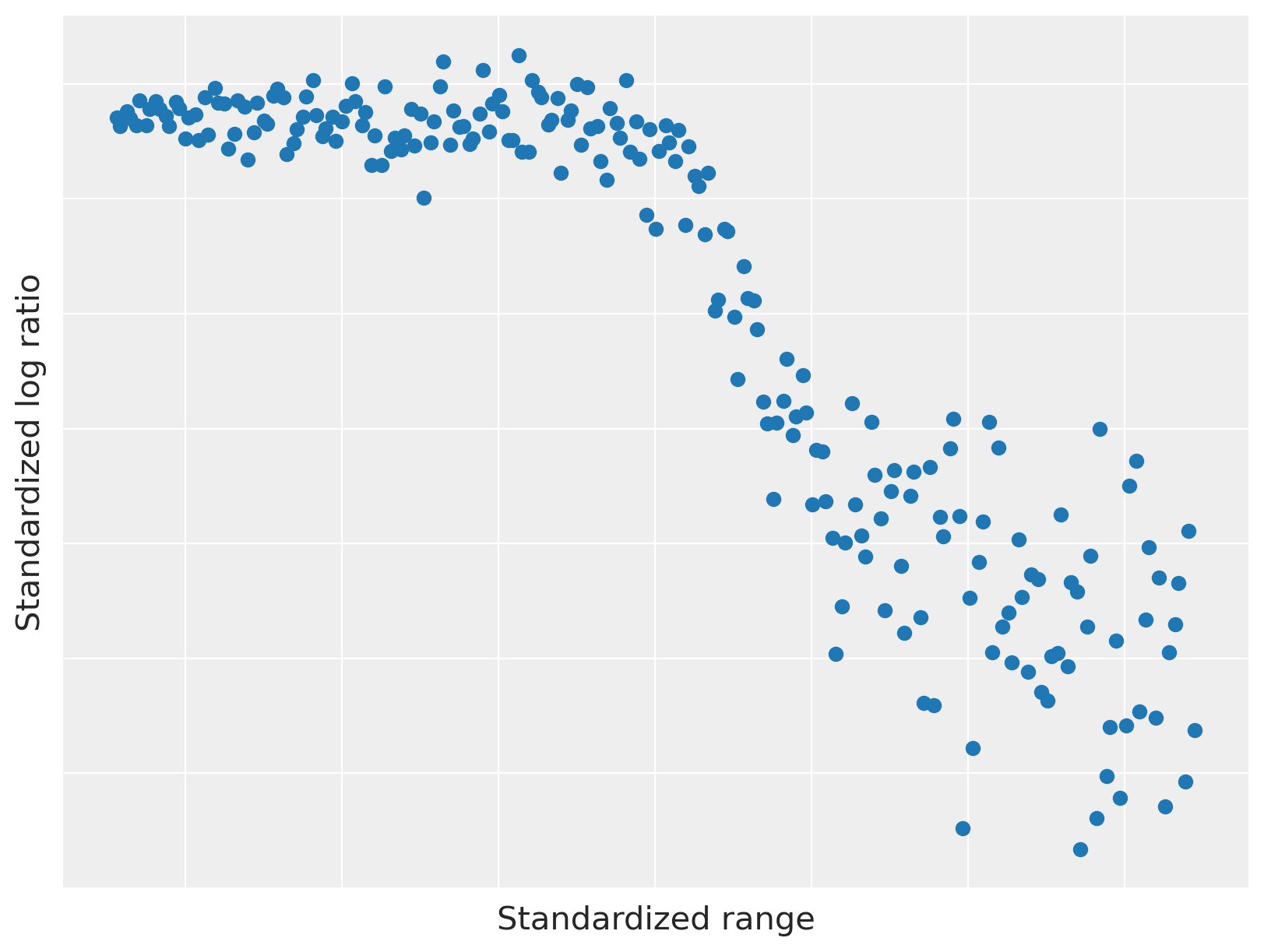
../_images/d394806a5d839fa0fa678227efd4e541486045dcdfb4a555b3749705848427b1.png

此数据集具有两个有趣的特性，使其适用于说明依赖密度回归。

范围与对数比之间的关系是非线性的，但具有局部线性成分。
观测噪声是异方差的；即，方差的大小随范围变化。

依赖密度回归背后的直观想法是将问题简化为许多（相关的）密度估计，这些估计是基于预测变量的固定值进行的。下面的动画说明了这种直觉。

fig, (scatter_ax, hist_ax) = plt.subplots(ncols=2, figsize=(16, 6))

scatter_ax.scatter(df.std_range, df.std_logratio, color=blue, zorder=2)

scatter_ax.set_xticklabels([])
scatter_ax.set_xlabel("Standardized range")

scatter_ax.set_yticklabels([])
scatter_ax.set_ylabel("Standardized log ratio")

bins = np.linspace(df.std_range.min(), df.std_range.max(), 25)

hist_ax.hist(df.std_logratio, bins=bins, color="k", lw=0, alpha=0.25, label="All data")

hist_ax.set_xticklabels([])
hist_ax.set_xlabel("Standardized log ratio")

hist_ax.set_yticklabels([])
hist_ax.set_ylabel("Frequency")

hist_ax.legend(loc=2)

endpoints = np.linspace(1.05 * df.std_range.min(), 1.05 * df.std_range.max(), 15)

frame_artists = []

for low, high in zip(endpoints[:-1], endpoints[2:]):
    interval = scatter_ax.axvspan(low, high, color="k", alpha=0.5, lw=0, zorder=1)
    *_, bars = hist_ax.hist(
        df[df.std_range.between(low, high)].std_logratio, bins=bins, color="k", lw=0, alpha=0.5
    )

    frame_artists.append((interval,) + tuple(bars))

animation = ani.ArtistAnimation(fig, frame_artists, interval=500, repeat_delay=3000, blit=True)
plt.close()
# prevent the intermediate figure from showing

HTML(animation.to_html5_video())

当我们沿着x轴滑动窗口对左侧图中的数据进行切片时，右侧图中窗口内点的y值的经验分布会发生变化。这种方法的一个重要方面是，对应于接近预测值的密度估计是相似的。

在之前的例子中，我们看到Dirichlet过程将概率密度估计为一个具有无限多个成分的混合模型。在成分分布为正态分布的情况下，

\[y \sim \sum_{i = 1}^{\infty} w_i \cdot N(\mu_i, \tau_i^{-1}),\]

其中混合权重, \(w_1, w_2, \ldots\), 是由stick-breaking process生成的。

依赖密度回归通过允许混合权重和成分均值根据预测值\(x\)的条件变化，推广了Dirichlet过程混合模型的这种表示。也就是说，

\[y\ |\ x \sim \sum_{i = 1}^{\infty} w_i\ |\ x \cdot N(\mu_i\ |\ x, \tau_i^{-1}).\]

在这个例子中，我们将遵循贝叶斯数据分析的第23章，并使用一个probit stick-breaking过程来确定条件混合权重，\(w_i\ |\ x\)。probit stick-breaking过程首先定义

\[v_i\ |\ x = \Phi(\alpha_i + \beta_i x),\]

其中 \(\Phi\) 是标准正态分布的累积分布函数。然后我们通过将stick breaking过程应用于 \(v_i\ |\ x\) 来获得 \(w_i\ |\ x\)。即，

\[w_i\ |\ x = v_i\ |\ x \cdot \prod_{j = 1}^{i - 1} (1 - v_j\ |\ x).\]

对于LIDAR数据集，我们使用独立的正态先验 \(\alpha_i \sim N(0, 5^2)\) 和 \(\beta_i \sim N(0, 5^2)\)。我们现在使用 PyMC3 来表达这个条件混合权重的模型。

def norm_cdf(z):
    return 0.5 * (1 + tt.erf(z / np.sqrt(2)))


def stick_breaking(v):
    return v * tt.concatenate(
        [tt.ones_like(v[:, :1]), tt.extra_ops.cumprod(1 - v, axis=1)[:, :-1]], axis=1
    )

N = len(df)
K = 20

std_range = df.std_range.values[:, np.newaxis]
std_logratio = df.std_logratio.values

with pm.Model(coords={"N": np.arange(N), "K": np.arange(K) + 1, "one": [1]}) as model:
    alpha = pm.Normal("alpha", 0.0, 5.0, dims="K")
    beta = pm.Normal("beta", 0.0, 5.0, dims=("one", "K"))
    x = pm.Data("x", std_range)
    v = norm_cdf(alpha + pm.math.dot(x, beta))
    w = pm.Deterministic("w", stick_breaking(v), dims=["N", "K"])

我们已经将 x 定义为一个 pm.Data 容器，以便稍后使用 PyMC3 的后验预测能力。

虽然依赖密度回归模型在理论上具有无限多个成分，但为了使用PyMC3表示该模型，我们必须将其截断为有限多个成分（在这种情况下，二十个）。在从模型中采样后，我们将验证截断没有不当地影响我们的结果。

由于LIDAR数据似乎有几个线性成分，我们使用线性模型

\[\begin{split} \begin{align*} \mu_i\ |\ x & \sim \gamma_i + \delta_i x \\ \gamma_i & \sim N(0, 10^2) \\ \delta_i & \sim N(0, 10^2) \end{align*} \end{split}\]

用于条件组件的含义。

with model:
    gamma = pm.Normal("gamma", 0.0, 10.0, dims="K")
    delta = pm.Normal("delta", 0.0, 10.0, dims=("one", "K"))
    mu = pm.Deterministic("mu", gamma + pm.math.dot(x, delta))

最后，我们在组件精度上放置先验 \(\tau_i \sim \textrm{Gamma}(1, 1)\)。

with model:
    tau = pm.Gamma("tau", 1.0, 1.0, dims="K")
    y = pm.Data("y", std_logratio)
    obs = pm.NormalMixture("obs", w, mu, tau=tau, observed=y)

pm.model_to_graphviz(model)

../_images/9ca363a70ba96b04a7ae215216e3926c34fda3b767784332d8bb0e93ad1e8047.svg

我们现在从依赖密度回归模型中进行采样。

SAMPLES = 20000
BURN = 10000

with model:
    step = pm.Metropolis()
    trace = pm.sample(SAMPLES, tune=BURN, step=step, random_seed=SEED, return_inferencedata=True)

100.00% [30000/30000 02:56<00:00 Sampling chain 0, 0 divergences]

100.00% [30000/30000 02:50<00:00 Sampling chain 1, 0 divergences]

为了验证截断没有不当地影响我们的结果，我们绘制了每个成分的最大后验期望混合权重。（在这个模型中，每个点对每个成分都有一个混合权重，因此我们绘制了所有数据点中每个成分的最大混合权重，以判断该成分是否对后验有任何影响。）

fig, ax = plt.subplots(figsize=(8, 6))

max_mixture_weights = trace.posterior["w"].mean(("chain", "draw")).max("N")
ax.bar(max_mixture_weights.coords.to_index(), max_mixture_weights)

ax.set_xlim(1 - 0.5, K + 0.5)
ax.set_xticks(np.arange(0, K, 2) + 1)
ax.set_xlabel("Mixture component")

ax.set_ylabel("Largest posterior expected\nmixture weight");

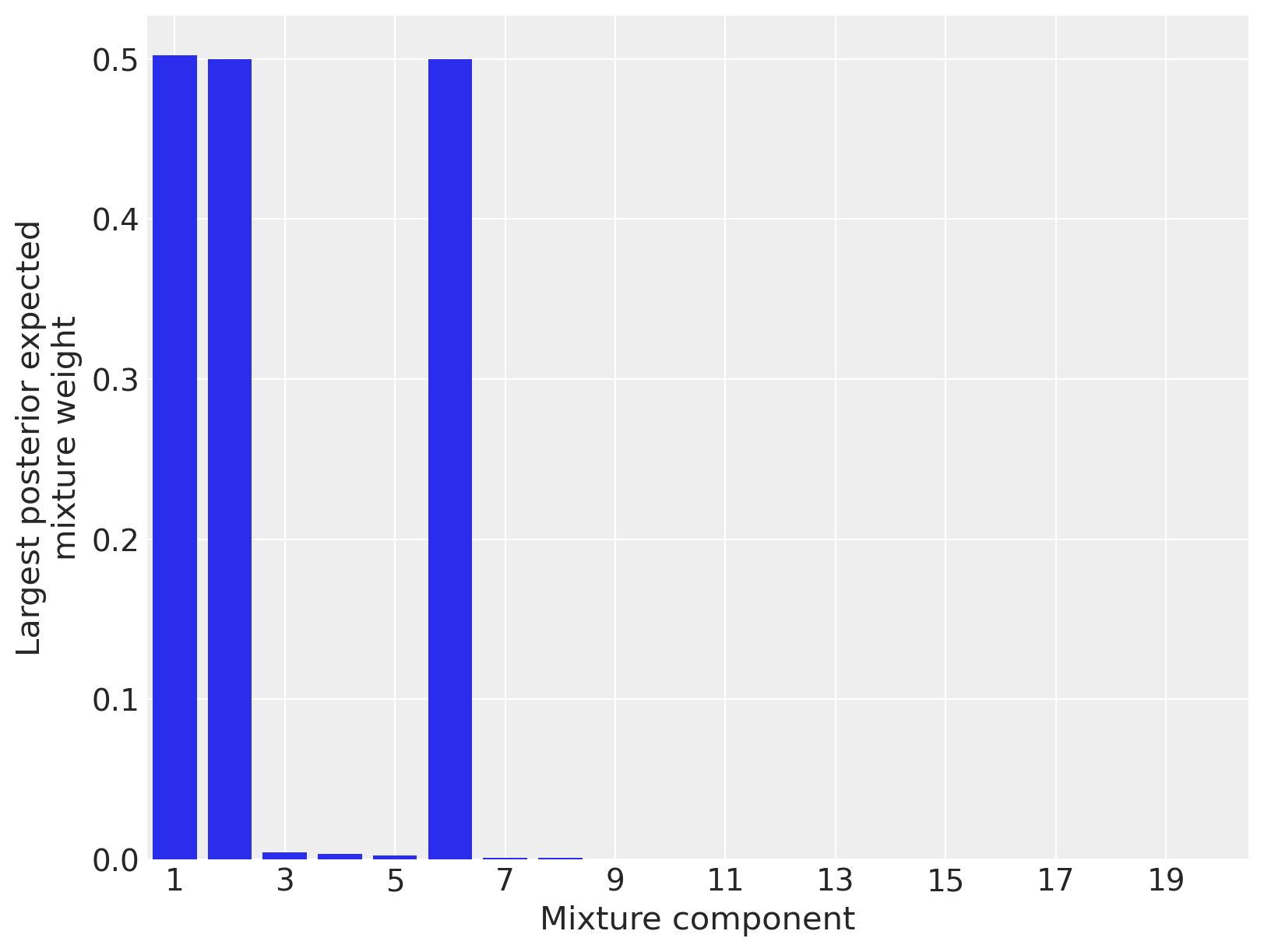
../_images/085411e242e51ac27509bd82a47cd037680fab3b873ad7727b42ac635fc130a4.png

由于只有三个混合成分对任何数据点都有显著的后验期望权重，我们可以相当确定截断并没有不当地影响我们的结果。（如果大多数成分都有显著的后验期望权重，截断可能会影响结果，我们将增加成分的数量并重新采样。）

从视觉上看，LIDAR数据具有三个线性成分是合理的，因此这些后验期望权重似乎很好地识别了数据的结构。我们现在从后验预测分布中进行采样，以更好地了解模型的性能。

PP_SAMPLES = 5000

lidar_pp_x = np.linspace(std_range.min() - 0.05, std_range.max() + 0.05, 100)

with model:
    pm.set_data({"x": lidar_pp_x[:, np.newaxis]})
    pp_trace = pm.sample_posterior_predictive(trace, PP_SAMPLES, random_seed=SEED)

/opt/conda/lib/python3.7/site-packages/pymc3/sampling.py:1690: UserWarning: samples parameter is smaller than nchains times ndraws, some draws and/or chains may not be represented in the returned posterior predictive sample
  "samples parameter is smaller than nchains times ndraws, some draws "

100.00% [5000/5000 03:23<00:00]

下面我们绘制后验期望值和95%后验可信区间。

fig, ax = plt.subplots(figsize=(8, 6))

ax.scatter(df.std_range, df.std_logratio, color=blue, zorder=10, label=None)

low, high = np.percentile(pp_trace["obs"], [2.5, 97.5], axis=0)
ax.fill_between(
    lidar_pp_x, low, high, color="k", alpha=0.35, zorder=5, label="95% posterior credible interval"
)

ax.plot(lidar_pp_x, pp_trace["obs"].mean(axis=0), c="k", zorder=6, label="Posterior expected value")

ax.set_xticklabels([])
ax.set_xlabel("Standardized range")

ax.set_yticklabels([])
ax.set_ylabel("Standardized log ratio")

ax.legend(loc=1)
ax.set_title("LIDAR Data");

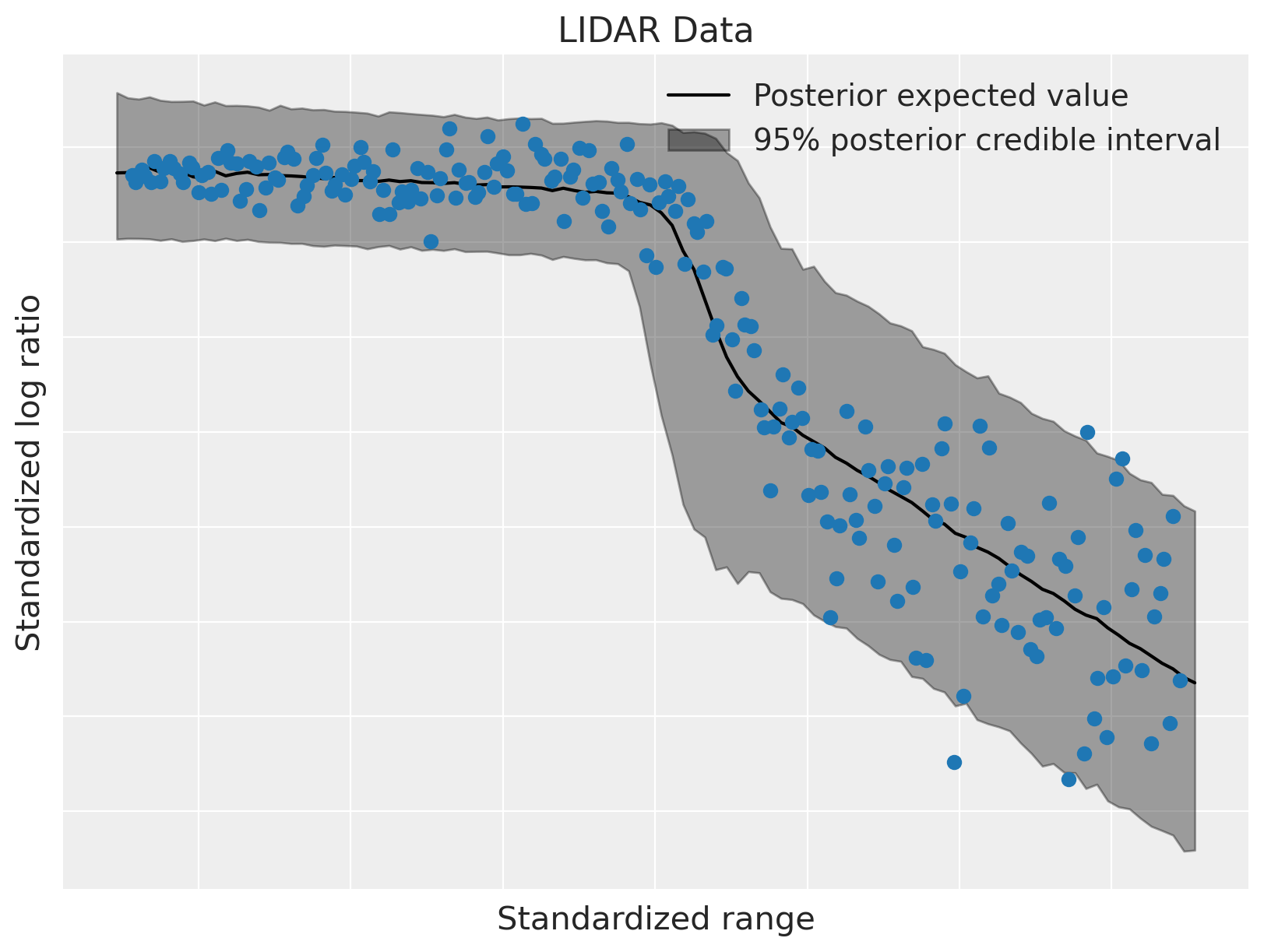
../_images/65f959215ef28b7439a3c08b9c69137a4a3da5f5706083108a994d0d69f7cf22.png

该模型很好地拟合了数据的线性成分，并且也适应了其异方差性。这种灵活性，以及能够模块化地指定条件混合权重和条件成分密度的能力，使得依赖密度回归成为一个非常有用的非参数贝叶斯模型。

要了解更多关于依赖密度回归及相关模型的信息，请参阅贝叶斯数据分析、贝叶斯非参数数据分析或贝叶斯非参数。

此示例首次出现在这里。

作者: Austin Rochford

%load_ext watermark
%watermark -n -u -v -iv -w

Last updated: Sat Apr 24 2021

Python implementation: CPython
Python version       : 3.7.6
IPython version      : 7.13.0

numpy     : 1.17.5
matplotlib: 3.2.1
pymc3     : 3.11.2
arviz     : 0.11.2
theano    : 1.1.2
pandas    : 1.1.5
seaborn   : 0.10.0

Watermark: 2.2.0

分类

标签

依赖密度回归#