Bloch-Redfield主方程
介绍
之前介绍的Lindblad主方程是为了描述密度矩阵的物理演化(即保持迹和正定性)而构建的,但它并没有提供与任何基础微观物理模型的联系。 Lindblad算子(坍缩算子)描述了现象学过程,例如退相干和自旋翻转,这些过程的速率是模型中的任意参数。 在许多情况下,坍缩算子及其相应的速率具有明确的物理解释,例如退相干和弛豫速率,在这些情况下,Lindblad主方程通常是首选方法。
然而,在某些情况下,例如具有变化的能量偏差和本征态的系统,并且以某种明确的方式与环境耦合(通过物理动机的系统-环境相互作用算子),通常希望从更基本的物理原理推导出主方程,并将其与环境噪声功率谱等相关联。
布洛赫-雷德菲尔德形式主义是一种从微观系统推导主方程的方法。 它从系统-环境的组合视角出发,在系统-环境耦合较弱的假设下,推导出仅针对系统的微扰主方程。 这种方法的一个优点是耗散过程和速率直接来自环境的特性。 缺点是它本身并不保证所得到的主方程无条件地保持密度矩阵的物理特性(因为它是一种微扰方法)。 因此,布洛赫-雷德菲尔德主方程必须谨慎使用,并且必须遵守推导中所做的假设。 (林德布拉德主方程在某种意义上更为稳健——它总是产生物理密度矩阵——尽管某些坍缩算子可能没有物理依据)。 有关布洛赫-雷德菲尔德主方程的完整推导,请参见例如 [Coh92] 或 [Bre02]。 这里我们仅提供一个简短的推导版本,目的是介绍符号及其与QuTiP中实现的关系。
简要推导和定义
Bloch-Redfield 形式论的起点是系统和环境(浴)的总哈密顿量:\(H = H_{\rm S} + H_{\rm B} + H_{\rm I}\),其中 \(H\) 是系统+浴的总哈密顿量,\(H_{\rm S}\) 和 \(H_{\rm B}\) 分别是系统和浴的哈密顿量,\(H_{\rm I}\) 是相互作用哈密顿量。
系统动力学的主方程的最一般形式是通过从组合系统的冯·诺伊曼运动方程(\(\dot\rho = -i\hbar^{-1}[H, \rho]\))中追踪出浴来获得的。在相互作用图中,结果是
其中附加假设是总系统-浴密度矩阵可以分解为 \(\rho(t) \approx \rho_S(t) \otimes \rho_B\)。 这一假设被称为玻恩近似,它意味着系统与浴之间从未存在任何纠缠,无论是在初始状态还是在演化过程中的任何时间。 这对于弱系统-浴相互作用是合理的。
主方程 (1) 是非马尔可夫的,即在时间 \(t\) 处的密度矩阵的变化依赖于所有时间 \(\tau < t\) 的状态,这使得它在理论上和数值上都难以求解。 为了朝着一个可管理的主方程迈进,我们现在引入马尔可夫近似,其中在方程 (1) 中,\(\rho_S(\tau)\) 被替换为 \(\rho_S(t)\)。 结果是Redfield方程
这是关于密度矩阵在时间上的局部性,但仍然不是马尔可夫的,因为它包含对初始状态的隐式依赖。通过将积分扩展到无穷大并替换\(\tau \rightarrow t-\tau\),可以得到一个完全马尔科夫的主方程:
如果系统动力学变化的时间尺度与浴中相关性衰减的时间尺度相比很大(对应于“短记忆”浴,这导致马尔可夫系统动力学),则上述两种马尔可夫近似是有效的。
主方程 (3) 的形式仍然过于一般化,不适合进行数值实现。因此,我们假设系统-浴相互作用的形式为 \(H_I = \sum_\alpha A_\alpha \otimes B_\alpha\),其中 \(A_\alpha\) 是系统算符,\(B_\alpha\) 是浴算符。这使得我们可以用系统算符和浴相关函数来表示主方程:
其中 \(g_{\alpha\beta}(\tau) = {\rm Tr}_B\left[B_\alpha(t)B_\beta(t-\tau)\rho_B\right] = \left
在系统哈密顿量的本征基中,其中 \(A_{mn}(t) = A_{mn} e^{i\omega_{mn}t}\), \(\omega_{mn} = \omega_m - \omega_n\) 且 \(\omega_m\) 是对应于本征态 \(\left|m\right>\) 的本征频率,我们在薛定谔绘景中以矩阵形式得到
其中求和符号上方的“sec”表示对满足 \(|\omega_{ab}-\omega_{cd}| \ll \tau_ {\rm decay}\) 的长期项进行求和。 这是一个几乎有用的主方程形式。在达到QuTiP中实现的Bloch-Redfield主方程形式之前,最后一步涉及将浴相关函数 \(g(\tau)\) 重写为环境的噪声功率谱 \(S(\omega) = \int_{-\infty}^\infty d\tau e^{i\omega\tau} g(\tau)\):
其中 \(\lambda_{ab}(\omega)\) 是一个在这里被忽略的能量偏移。布洛赫-雷德菲尔德主方程的最终形式是
其中
是 Bloch-Redfield 张量。
Bloch-Redfield主方程的形式如公式(5)所示,适用于数值实现。输入参数包括系统哈密顿量\(H\)、系统通过环境耦合到系统的操作符\(A_\alpha\),以及与每个系统-环境相互作用项相关的噪声功率谱\(S_{\alpha\beta}(\omega)\)。
为了简化数值实现,我们假设\(A_\alpha\)是厄米特矩阵,并且不同环境算子之间的互相关消失,因此在QuTiP中实现的Bloch-Redfield张量的最终表达式为
QuTiP中的Bloch-Redfield主方程
在QuTiP中,Bloch-Redfield张量方程 (7) 可以使用函数 bloch_redfield_tensor 计算。
它需要两个必需的参数:系统哈密顿量 \(H\),一个操作符 \(A_\alpha\) 的嵌套列表,以及表征系统与浴之间耦合的谱密度函数 \(S_\alpha(\omega)\) 对。
谱密度函数是Python回调函数,它以(角)频率作为单个参数。
为了说明如何计算Bloch-Redfield张量,让我们考虑一个两能级原子
delta = 0.2 * 2*np.pi
eps0 = 1.0 * 2*np.pi
gamma1 = 0.5
H = - delta/2.0 * sigmax() - eps0/2.0 * sigmaz()
def ohmic_spectrum(w):
if w == 0.0: # dephasing inducing noise
return gamma1
else: # relaxation inducing noise
return gamma1 / 2 * (w / (2 * np.pi)) * (w > 0.0)
R, ekets = bloch_redfield_tensor(H, a_ops=[[sigmax(), ohmic_spectrum]])
print(R)
输出:
Quantum object: dims = [[[2], [2]], [[2], [2]]], shape = (4, 4), type = super, isherm = False
Qobj data =
[[ 0. +0.j 0. +0.j 0. +0.j
0.24514517+0.j ]
[ 0. +0.j -0.16103412-6.4076169j 0. +0.j
0. +0.j ]
[ 0. +0.j 0. +0.j -0.16103412+6.4076169j
0. +0.j ]
[ 0. +0.j 0. +0.j 0. +0.j
-0.24514517+0.j ]]
请注意,也可以通过c_ops关键字参数传递操作符来在Bloch-Redfield张量中添加Lindblad耗散超算符,就像在mesolve或mcsolve函数中一样。为了方便起见,函数bloch_redfield_tensor还会返回基变换操作符和特征向量矩阵,因为它们在计算Bloch-Redfield张量R的过程中被计算出来,并且ekets通常在稍后将操作符在实验室基和特征基之间转换时再次需要。通过设置fock_basis=True可以在实验室基中获得张量,在这种情况下,不会返回变换操作符。
根据Bloch-Redfield主方程(5),波函数或密度矩阵的演化可以使用QuTiP函数mesolve在实验室基中使用Bloch-Redfield张量而不是Liouvillian来计算。例如,为了评估上述示例中\(\sigma_x\)、\(\sigma_y\)和\(\sigma_z\)算符的期望值,我们可以使用以下代码:
delta = 0.2 * 2*np.pi
eps0 = 1.0 * 2*np.pi
gamma1 = 0.5
H = - delta/2.0 * sigmax() - eps0/2.0 * sigmaz()
def ohmic_spectrum(w):
if w == 0.0: # dephasing inducing noise
return gamma1
else: # relaxation inducing noise
return gamma1 / 2 * (w / (2 * np.pi)) * (w > 0.0)
R = bloch_redfield_tensor(H, [[sigmax(), ohmic_spectrum]], fock_basis=True)
tlist = np.linspace(0, 15.0, 1000)
psi0 = rand_ket(2, seed=1)
e_ops = [sigmax(), sigmay(), sigmaz()]
expt_list = mesolve(R, psi0, tlist, e_ops=e_ops).expect
sphere = Bloch()
sphere.add_points([expt_list[0], expt_list[1], expt_list[2]])
sphere.vector_color = ['r']
sphere.add_vectors(np.array([delta, 0, eps0]) / np.sqrt(delta ** 2 + eps0 ** 2))
sphere.make_sphere()
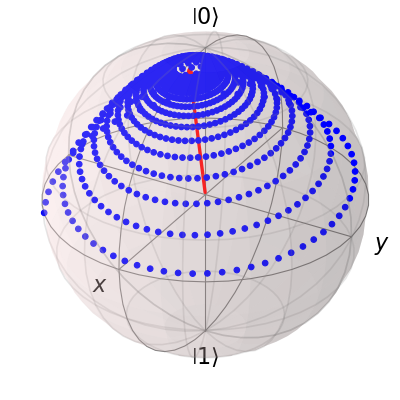
计算Bloch-Redfield张量并根据相应的主方程演化的两个步骤可以通过使用函数brmesolve合并为一个步骤,该函数接受与mesolve和mcsolve相同的参数,除了称为a_ops的额外嵌套列表的算子-频谱对。
output = brmesolve(H, psi0, tlist, a_ops=[[sigmax(),ohmic_spectrum]], e_ops=e_ops)
其中生成的输出是类Result的一个实例。
注意
虽然代码示例模拟了在世俗近似下的Bloch-Redfield方程,QuTiP的实现允许用户通过设置sec_cutoff=-1来模拟非世俗版本的Bloch-Redfield方程,以及通过将其设置为float来进行部分世俗近似,这个浮点数将成为(5)中求和的截止值,意味着大于截止值的\(|\omega_{ab}-\omega_{cd}|\)项将被忽略。其默认值为0.1,对应于世俗近似。例如,命令
output = brmesolve(H, psi0, tlist, a_ops=[[sigmax(), ohmic_spectrum]],
e_ops=e_ops, sec_cutoff=-1)
将模拟与上述相同的例子,但不使用长期近似。 请注意,使用非长期版本可能会导致负值问题。
时间依赖的Bloch-Redfield动力学
如果您还没有这样做,请阅读以下部分:解决随时间变化的哈密顿量问题。
正如我们已经讨论过的,Bloch-Redfield主方程需要转换到系统哈密顿量的本征基中。对于时间无关的系统,这种转换只需要进行一次。然而,对于时间相关的系统,必须在演化的每个时间步长移动到瞬时本征基,从而大大增加了动力学的计算复杂性。此外,计算所有本征值的要求严重限制了该方法的可扩展性。幸运的是,这种本征分解发生在哈密顿量级别,而不是超算子级别,因此,通过高效的编程,可以处理许多常见的系统。
对于时间依赖的哈密顿量,哈密顿量本身可以像任何其他时间依赖的哈密顿量一样传递给求解器,因此我们将不再进一步讨论这个话题。相反,这里的重点是时间依赖的浴耦合项。为此,假设我们有一个耗散谐波振荡器,其中白噪声耗散率随时间指数下降 \(\kappa(t) = \kappa(0)\exp(-t)\)。在Lindblad或Monte Carlo求解器中,这可以实现为时间依赖的崩溃算子列表 c_ops = [[a, 'sqrt(kappa*exp(-t))']]。在Bloch-Redfield求解器中,浴耦合项必须是厄米的。因此,在这个例子中,我们的耦合算子是位置算子 a+a.dag()。完整的例子,以及与解析表达式的比较是:
N = 10 # number of basis states to consider
a = destroy(N)
H = a.dag() * a
psi0 = basis(N, 9) # initial state
kappa = 0.2 # coupling to oscillator
a_ops = [
([a+a.dag(), f'sqrt({kappa}*exp(-t))'], '(w>=0)')
]
tlist = np.linspace(0, 10, 100)
out = brmesolve(H, psi0, tlist, a_ops, e_ops=[a.dag() * a])
actual_answer = 9.0 * np.exp(-kappa * (1.0 - np.exp(-tlist)))
plt.figure()
plt.plot(tlist, out.expect[0])
plt.plot(tlist, actual_answer)
plt.show()
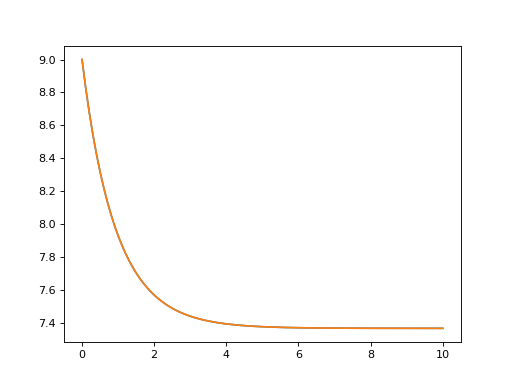
在许多情况下,浴耦合算子可以采取形式 \(A = f(t)a + f(t)^* a^{+}\)。
a_ops 的算子部分可以由尽可能多的时间相关项组成,以构建这样的算子。
例如,考虑一个白噪声浴,它与形式为 exp(1j*t)*a + exp(-1j*t)* a.dag() 的算子耦合。
在这个例子中,a_ops 列表将是:
a_ops = [
([[a, 'exp(1j*t)'], [a.dag(), 'exp(-1j*t)']], f'{kappa} * (w >= 0)')
]
其中第一个元组元素 [[a, 'exp(1j*t)'], [a.dag(), 'exp(-1j*t)']] 告诉求解器什么是时间依赖的厄米耦合算子。
第二个元组 f'{kappa} * (w >= 0)' 给出了噪声功率谱。
一个完整的例子是:
N = 10
w0 = 1.0 * 2 * np.pi
g = 0.05 * w0
kappa = 0.15
times = np.linspace(0, 25, 1000)
a = destroy(N)
H = w0 * a.dag() * a + g * (a + a.dag())
psi0 = ket2dm((basis(N, 4) + basis(N, 2) + basis(N, 0)).unit())
a_ops = [[
QobjEvo([[a, 'exp(1j*t)'], [a.dag(), 'exp(-1j*t)']]), (f'{kappa} * (w >= 0)')
]]
e_ops = [a.dag() * a, a + a.dag()]
res_brme = brmesolve(H, psi0, times, a_ops, e_ops=e_ops)
plt.figure()
plt.plot(times, res_brme.expect[0], label=r'$a^{+}a$')
plt.plot(times, res_brme.expect[1], label=r'$a+a^{+}$')
plt.legend()
plt.show()
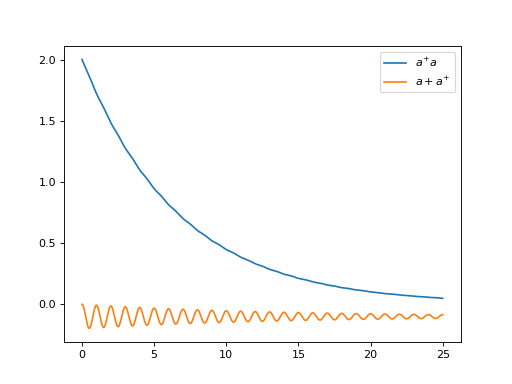
关于时间依赖的Bloch-Redfield模拟的更多示例可以在在线教程中找到。