求解器类接口

在QuTiP版本5及更高版本中，诸如mesolve、mcsolve等求解器也具有类接口。类接口允许重用哈密顿量并微调求解器运行的许多细节。

下面给出了一些求解器类功能的示例。

重用哈密顿数据

在许多情况下，人们希望研究同一量子系统的多次演化，无论是通过改变初始状态还是其他参数。为了尽可能快地演化给定的系统，QuTiP中的求解器会接收给定的输入算子（哈密顿量、崩溃算子等），并为所选的ODE求解器做好准备。

这些操作通常相当快，但对于一些求解器，例如 brmesolve 或 fmmesolve，开销可能很大。 即使对于更简单的求解器，当重复求解系统时，组织数据所花费的时间也可能变得相当可观。

类接口允许我们一次性设置系统，并使用各种参数重复使用它。大多数...solve函数都有一个配对的...Solver类，其中包含一个..Solver.run方法来运行演化。在类实例创建时，物理参数（H、c_ops、a_ops等）和选项会被传递。初始状态、时间和期望操作符仅在调用run时传递：

times = np.linspace(0.0, 6.0, 601)
a  = tensor(qeye(2), destroy(10))
sm = tensor(destroy(2), qeye(10))
e_ops = [a.dag() * a, sm.dag() * sm]
H = QobjEvo(
    [a.dag()*a + sm.dag()*sm, [(sm*a.dag() + sm.dag()*a), lambda t, A: A]],
    args={"A": 0.5*np.pi}
)

solver = MESolver(H, c_ops=[np.sqrt(0.1) * a], options={"atol": 1e-8})
solver.options["normalize_output"] = True
psi0 = tensor(fock(2, 0), fock(10, 5))
data1 = solver.run(psi0, times, e_ops=e_ops)
psi1 = tensor(fock(2, 0), coherent(10, 2 - 1j))
data2 = solver.run(psi1, times, e_ops=e_ops)

plt.figure()
plt.plot(times, data1.expect[0], "b", times, data1.expect[1], "r", lw=2)
plt.plot(times, data2.expect[0], 'b--', times, data2.expect[1], 'r--', lw=2)
plt.title('Master Equation time evolution')
plt.xlabel('Time', fontsize=14)
plt.ylabel('Expectation values', fontsize=14)
plt.legend(("cavity photon number", "atom excitation probability"))
plt.show()
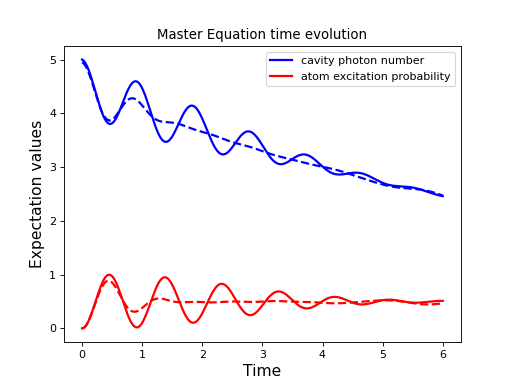
../../_images/dynamics-class-1.png

请注意，如图所示，选项可以在初始化时设置，也可以通过options属性进行设置。

模拟参数，即作为系统操作符传递的QobjEvo的args，可以在运行开始时更新：

data1 = solver.run(psi0, times, e_ops=e_ops)
data2 = solver.run(psi0, times, e_ops=e_ops, args={"A": 0.25*np.pi})
data3 = solver.run(psi0, times, e_ops=e_ops, args={"A": 0.125*np.pi})

plt.figure()
plt.plot(times, data1.expect[0], label="A=pi/2")
plt.plot(times, data2.expect[0], label="A=pi/4")
plt.plot(times, data3.expect[0], label="A=pi/8")
plt.title('Master Equation time evolution')
plt.xlabel('Time', fontsize=14)
plt.ylabel('Expectation values', fontsize=14)
plt.legend()
plt.show()
../../_images/dynamics-class-2.png

逐步执行运行

求解器类还允许逐步运行模拟，每一步更新参数：

data = [5.]
solver.start(state0=psi0, t0=times[0])
for t in times[1:]:
    psi_t = solver.step(t, args={"A": np.pi*np.exp(-(t-3)**2)})
    data.append(expect(e_ops[0], psi_t))

plt.figure()
plt.plot(times, data)
plt.title('Master Equation time evolution')
plt.xlabel('Time', fontsize=14)
plt.ylabel('Expectation values', fontsize=14)
plt.legend(("cavity photon number"))
plt.show()
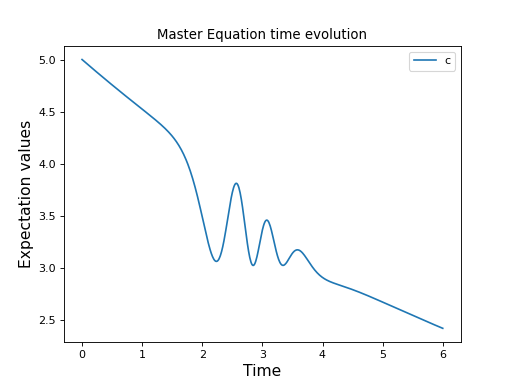
../../_images/dynamics-class-3.png

注意

这只是一个示例，在步骤之间更新常量 args 参数不应替换使用函数作为 QobjEvo 的系数。

注意

可以创建多个求解器，并使用step并行推进它们。然而，许多ODE求解器，包括默认的adams方法，每个进程一次只允许一个实例。QuTiP支持使用这些ODE求解器的多个实例，但会有性能成本。在这些情况下，建议使用dop853或vern9积分方法。

反馈：从演化算子访问求解器状态

系统在演化过程中的状态可以通过求解器类的属性访问。

每个求解器都有一个StateFeedback和ExpectFeedback类方法，可以作为参数传递给时间依赖系统。例如，ExpectFeedback可以用于创建一个在腔体内有5个或更少光子时解耦的系统。

def f(t, e1):
    ex = (e1.real - 5)
    return (ex > 0) * ex * 10

times = np.linspace(0.0, 1.0, 301)
a  = tensor(qeye(2), destroy(10))
sm = tensor(destroy(2), qeye(10))
e_ops = [a.dag() * a, sm.dag() * sm]
psi0 = tensor(fock(2, 0), fock(10, 8))
e_ops = [a.dag() * a, sm.dag() * sm]

H = [a*a.dag(), [sm*a.dag() + sm.dag()*a, f]]
data = mesolve(H, psi0, times, c_ops=[a], e_ops=e_ops,
    args={"e1": MESolver.ExpectFeedback(a.dag() * a)}
).expect

plt.figure()
plt.plot(times, data[0])
plt.plot(times, data[1])
plt.title('Master Equation time evolution')
plt.xlabel('Time', fontsize=14)
plt.ylabel('Expectation values', fontsize=14)
plt.legend(("cavity photon number", "atom excitation probability"))
plt.show()
../../_images/dynamics-class-4.png