随机求解器

当一个量子系统受到连续测量时，例如通过同调检测，可以使用随机薛定谔方程和主方程来模拟条件量子态。这些随机方程的解是量子轨迹，它们代表了在给定特定测量记录下系统的条件演化。

一般来说，量子态的随机演化在QuTiP中是通过求解一般方程来计算的

(1)\[d \rho (t) = d_1 \rho \, dt + \sum_n d_{2,n} \rho \, dW_n,\]

其中 \(dW_n\) 是一个维纳增量，其期望值为 \(E[dW] = 0\) 和 \(E[dW^2] = dt\)。

随机薛定谔方程

随机薛定谔方程由下式给出（参见第4.4节，[Wis09]）

(2)\[d \psi(t) = - i H \psi(t) dt - \sum_n \left( \frac{S_n^\dagger S_n}{2} -\frac{e_n}{2} S_n + \frac{e_n^2}{8} \right) \psi(t) dt + \sum_n \left( S_n - \frac{e_n}{2} \right) \psi(t) dW_n,\]

其中 \(H\) 是哈密顿量，\(S_n\) 是随机坍缩算子，\(e_n\) 是

(3)\[e_n = \left<\psi(t)|S_n + S_n^\dagger|\psi(t)\right>\]

在QuTiP中，可以使用函数ssesolve来求解这个方程，这是通过定义方程(1)中的\(d_1\)和\(d_{2,n}\)来实现的。

(4)\[d_1 = -iH - \frac{1}{2} \sum_n \left(S_n^\dagger S_n - e_n S_n + \frac{e_i^2}{4} \right),\]

和

(5)\[d_{2, n} = S_n - \frac{e_n}{2}.\]

求解器 ssesolve 将在用户传递哈密顿量 (H) 和随机算子列表 (sc_ops) 后构造算子 \(d_1\) 和 \(d_{2,n}\)。与 mcsolve 一样，轨迹数量和噪声实现的种子可以通过参数 ntraj 和 seeds 分别固定。如果用户还需要测量输出，则应包含选项条目 {"store_measurement": True}。

默认情况下，使用同调检测。通过将参数 'heterodyne=True' 传递给 ssesolve，可以轻松模拟异调检测。

随机主方程

当系统的初始状态是密度矩阵 \(\rho\) 时，必须使用随机主方程求解器 qutip.stochastic.smesolve。随机主方程由以下公式给出（参见第4.4节，[Wis09]）

(6)\[ d \rho (t) = -i[H, \rho(t)] dt + D[A]\rho(t) dt + \mathcal{H}[A]\rho dW(t)\]

其中

(7)\[D[A] \rho = \frac{1}{2} \left[2 A \rho A^\dagger - \rho A^\dagger A - A^\dagger A \rho \right],\]

和

(8)\[\mathcal{H}[A]\rho = A\rho(t) + \rho(t) A^\dagger - \mathrm{tr}[A\rho(t) + \rho(t) A^\dagger].\]

在QuTiP中，随机主方程的解是使用求解器smesolve获得的。该实现考虑了两种类型的坍缩算子。\(C_i\)（c_ops）表示环境中的耗散，而\(S_n\)（sc_ops）是被监测的算子。演化的确定性部分，由方程(1)中的\(d_1\)描述，考虑了所有算子\(C_i\)和\(S_n\)：

(9)\[d_1 = - i[H(t),\rho(t)] + \sum_i D[C_i]\rho + \sum_n D[S_n]\rho,\]

随机部分，\(d_{2,n}\)，仅由操作符\(S_n\)给出

(10)\[d_{2,n} = S_n \rho(t) + \rho(t) S_n^\dagger - \mathrm{tr}\left(S_n \rho (t) + \rho(t) S_n^\dagger \right)\,\rho(t).\]

与随机薛定谔方程中一样，可以通过传递heterodyne=True来选择外差检测。

示例

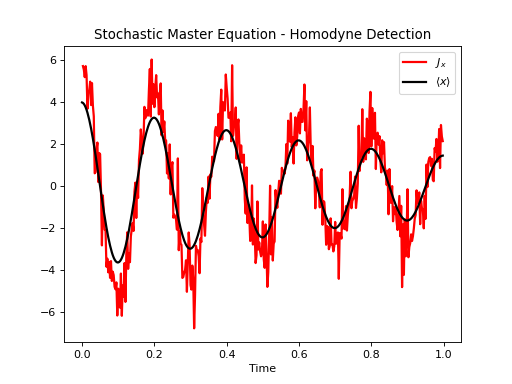
下面，我们解决了一个在0K下输出通过同调检测监控的光学腔的动力学问题。腔的衰减率由\(\kappa\)给出，而\(\Delta\)是腔相对于驱动场的失谐。同调电流\(J_x\)通过以下方式计算：

(11)\[J_x = \langle x \rangle + dW / dt,\]

其中 \(x\) 是从 sc_ops 构建的操作符

\[x_n = S_n + S_n^\dagger\]

结果可在 result.measurement 中获取。

# parameters
DIM = 20               # Hilbert space dimension
DELTA = 5 * 2 * np.pi  # cavity detuning
KAPPA = 2              # cavity decay rate
INTENSITY = 4          # intensity of initial state
NUMBER_OF_TRAJECTORIES = 500

# operators
a = destroy(DIM)
x = a + a.dag()
H = DELTA * a.dag() * a

rho_0 = coherent(DIM, np.sqrt(INTENSITY))
times = np.arange(0, 1, 0.0025)

stoc_solution = smesolve(
    H, rho_0, times,
    c_ops=[],
    sc_ops=[np.sqrt(KAPPA) * a],
    e_ops=[x],
    ntraj=NUMBER_OF_TRAJECTORIES,
    options={"dt": 0.00125, "store_measurement": True,}
)

fig, ax = plt.subplots()
ax.set_title('Stochastic Master Equation - Homodyne Detection')
ax.plot(times[1:], np.array(stoc_solution.measurement).mean(axis=0)[0, :].real,
        'r', lw=2, label=r'$J_x$')
ax.plot(times, stoc_solution.expect[0], 'k', lw=2,
        label=r'$\langle x \rangle$')
ax.set_xlabel('Time')
ax.legend()

从已知测量值运行

在不需要运行多个轨迹的情况下，我们希望从已知的噪声或实验室获得的测量结果中重现单个轨迹。在这些情况下，我们可以使用run_from_experiment。

让我们使用前一次模拟的第一条轨迹的测量输出 J_x 作为输入来重新计算一条轨迹：

# Create a stochastic solver instance with the some Hamiltonian as the
# previous evolution.
solver = SMESolver(
    H, sc_ops=[np.sqrt(KAPPA) * a],
    options={"dt": 0.00125, "store_measurement": True,}
)

# Run the evolution, noise
recreated_solution = solver.run_from_experiment(
    rho_0, tlist, stoc_solution.measurements[0],
    e_ops=[H],
    # The third parameter is the measurement, not the Wiener increment
    measurement=True,
)

这将重新计算该轨迹的状态、期望值和维纳增量。

注意

结果中的测量值默认是从时间步长结束时的状态计算的。然而，当使用run_from_experiment并输入测量值时，使用的是时间步长开始时的状态。要在smesolve的输出中获得时间步长开始时的测量值，可以使用选项{'store_measurement': 'start'}。

关于qutip.solver.stochastic.smesolve的其他示例，请参阅QuTiP教程页面上提供的笔记本：

随机求解器与mcsolve共享许多功能，例如结束条件、种子控制和并行运行。详情请参阅章节改变轨迹数量、可重复性和并行运行轨迹。