Krylov 求解器

介绍

Krylov子空间方法是近似量子动力学的标准方法。设\(\left|\psi\right\rangle\)为一个在\(D\)维复希尔伯特空间中的状态，该状态在时间无关的哈密顿量\(H\)下演化。那么，与该状态和哈密顿量相关的\(N\)维Krylov子空间由下式给出：

(1)\[\mathcal{K}_{N}=\operatorname{span}\left\{|\psi\rangle, H|\psi\rangle, \ldots, H^{N-1}|\psi\rangle\right\},\]

其中维度 \(N 是一个选择的参数。为了构建 \(\mathcal{K}_{N}\) 的正交基 \(B_N\)，最简单的算法是著名的Lanczos算法，它提供了一种类似于Gram-Schmidt过程的方法，利用只需要对基中的最后两个向量进行正交化的事实。在这个基中，时间演化的状态可以近似表示为

(2)\[|\psi(t)\rangle=e^{-iHt}|\psi\rangle\approx\mathbb{P}_{N}e^{-iHt}\mathbb{P}_{N}|\psi\rangle=\mathbb{V}_{N}^{\dagger}e^{-iT_{N}t}\mathbb{V}_{N}|\psi\rangle\equiv\left|\psi_{N}(t)\right\rangle,\]

其中 \(T_{N}=\mathbb{V}_{N} H \mathbb{V}_{N}^{\dagger}\) 是缩减到Krylov子空间的哈密顿量（它采用三对角矩阵形式），而 \(\mathbb{V}_{N}^{\dagger}\) 是包含Krylov基向量作为列的矩阵。

通过上述近似，时间演化仅使用所需大小的较小方阵进行计算。因此，当哈密顿量的维度非常大时，Krylov方法在短时间演化的计算中提供了巨大的加速，此时在完整子空间上进行精确计算实际上是不可能的。

这种方法最大的问题之一是误差的控制。经过很短的时间后，误差开始呈指数增长。然而，当误差达到某个阈值时，通过重新启动子空间可以轻松纠正这个问题。因此，一系列\(M\) Krylov子空间时间演化提供了完整时间演化的准确解。在这个方案中，Krylov的魔力不仅在于它能够从非常大的希尔伯特空间中捕捉复杂的时间演化，而且在于它提供的计算加速。

在特殊情况下，Lanczos算法可能会在维度\(M_{hb}时达到初始状态的精确演化。这被称为幸运崩溃。例如，如果哈密顿量有一个对称子空间\(D_{\text{sim}}，那么算法将使用值math:M_{hb}:进行优化，此时演化不仅是精确的，而且成本低廉。

QuTiP中的Krylov求解器

在QuTiP中，Krylov子空间演化是通过函数krylovsolve实现的。参数与sesolve函数几乎相同，用于主方程演化，除了哈密顿量不能依赖于时间，初始状态必须始终是一个ket向量（不能用于计算传播子），并且需要一个额外的参数krylov_dim。krylov_dim定义了允许的最大Krylov子空间维度。

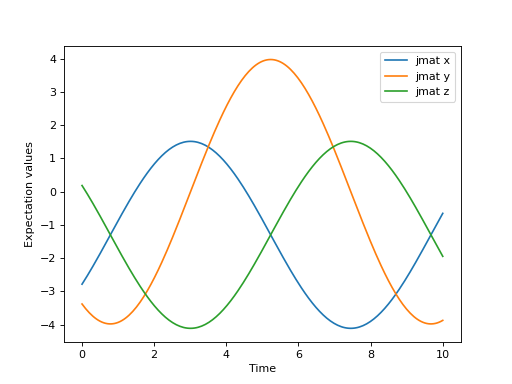
让我们通过使用QuTiP中的算法来解决一个简单的例子，以熟悉该方法。

>>> dim = 100
>>> jx = jmat((dim - 1) / 2.0, "x")
>>> jy = jmat((dim - 1) / 2.0, "y")
>>> jz = jmat((dim - 1) / 2.0, "z")
>>> e_ops = [jx, jy, jz]
>>> H = (jz + jx) / 2
>>> psi0 = rand_ket(dim, seed=1)
>>> tlist = np.linspace(0.0, 10.0, 200)
>>> results = krylovsolve(H, psi0, tlist, krylov_dim=20, e_ops=e_ops)
>>> plt.figure()
>>> for expect in results.expect:
>>>    plt.plot(tlist, expect)
>>> plt.legend(('jmat x', 'jmat y', 'jmat z'))
>>> plt.xlabel('Time')
>>> plt.ylabel('Expectation values')
>>> plt.show()