Floquet 形式主义

介绍

许多与时间相关的问题都是周期性的。这类系统的动力学可以通过直接数值积分薛定谔方程或主方程来求解，使用与时间相关的哈密顿量。但它们也可以通过弗洛凯形式转化为与时间无关的问题。与时间无关的问题可以更高效地解决，因此这种转化通常是非常可取的。

在Lindblad和Bloch-Redfield主方程的标准推导中，假设描述所考虑系统的哈密顿量是时间无关的。因此，严格来说，这些主方程形式的标准形式不应盲目地应用于具有时间依赖哈密顿量的系统。然而，在许多相关情况下，特别是对于弱驱动，标准主方程仍然对许多时间依赖问题有用。但更严格的方法是从一开始就考虑哈密顿量的时间依赖性，重新推导主方程。Floquet-Markov主方程就是这样一种形式，对于强驱动系统有重要应用（参见例如[Gri98]）。

在这里，我们概述了如何使用Floquet和Floquet-Markov形式主义来解决QuTiP中的时间相关问题。为了介绍QuTiP中使用的术语和命名约定，我们首先简要总结了量子Floquet理论。

Floquet理论用于酉演化

具有时间依赖哈密顿量 \(H(t)\) 的薛定谔方程为

(1)\[ H(t)\Psi(t) = i\hbar\frac{\partial}{\partial t}\Psi(t),\]

其中 \(\Psi(t)\) 是波函数解。这里我们关注的是具有周期性时间依赖性的问题，即哈密顿量满足 \(H(t) = H(t+T)\)，其中 \(T\) 是周期。根据Floquet定理，存在形式为 (1) 的解。

(2)\[ \Psi_\alpha(t) = \exp(-i\epsilon_\alpha t/\hbar)\Phi_\alpha(t),\]

其中 \(\Psi_\alpha(t)\) 是 Floquet 态（即薛定谔方程的一组波函数解），\(\Phi_\alpha(t)=\Phi_\alpha(t+T)\) 是周期性的 Floquet 模式，而 \(\epsilon_\alpha\) 是 准能级。准能级在时间上是常数，但仅在 \(2\pi/T\) 的倍数范围内唯一定义（即在区间 \([0, 2\pi/T]\) 内的唯一值）。

如果我们知道Floquet模式（对于\(t \in [0,T]\)）和特定\(H(t)\)的准能量，我们可以轻松地将任何初始波函数\(\Psi(t=0)\)分解为Floquet态，并立即得到任意\(t\)的解

(3)\[ \Psi(t) = \sum_\alpha c_\alpha \Psi_\alpha(t) = \sum_\alpha c_\alpha \exp(-i\epsilon_\alpha t/\hbar)\Phi_\alpha(t),\]

其中系数 \(c_\alpha\) 由初始波函数 \(\Psi(0) = \sum_\alpha c_\alpha \Psi_\alpha(0)\) 决定。

这种形式主义对于找到给定\(H(t)\)的\(\Psi(t)\)非常有用，前提是我们能够比直接求解(1)更容易地获得Floquet模式\(\Phi_a(t)\)和准能量\(\epsilon_\alpha\)。通过将(2)代入薛定谔方程(1)，我们得到了Floquet模式和准能量的特征值方程。

(4)\[ \mathcal{H}(t)\Phi_\alpha(t) = \epsilon_\alpha\Phi_\alpha(t),\]

其中 \(\mathcal{H}(t) = H(t) - i\hbar\partial_t\)。这个特征值问题可以解析或数值求解，但在QuTiP中，我们使用另一种方法来数值求解Floquet态和准能量[参见例如Creffield等人，Phys. Rev. B 67, 165301 (2003)]。考虑时间依赖的薛定谔方程的传播子 (1)，根据定义，它满足

\[U(T+t,t)\Psi(t) = \Psi(T+t).\]

将Floquet状态从(2)插入此表达式结果中

\[U(T+t,t)\exp(-i\epsilon_\alpha t/\hbar)\Phi_\alpha(t) = \exp(-i\epsilon_\alpha(T+t)/\hbar)\Phi_\alpha(T+t),\]

或者，因为 \(\Phi_\alpha(T+t)=\Phi_\alpha(t)\),

\[U(T+t,t)\Phi_\alpha(t) = \exp(-i\epsilon_\alpha T/\hbar)\Phi_\alpha(t) = \eta_\alpha \Phi_\alpha(t),\]

这表明Floquet模式是一周期传播子的本征态。因此，我们可以通过数值计算\(U(T+t,t)\)并对其进行对角化来找到Floquet模式和准能量\(\epsilon_\alpha = -\hbar\arg(\eta_\alpha)/T\)。特别是，这种方法通过计算和对角化\(U(T,0)\)来找到\(\Phi_\alpha(0)\)非常有用。

任意时间 \(t\) 的 Floquet 模式可以通过使用波函数传播器 \(U(t,0)\Psi_\alpha(0) = \Psi_\alpha(t)\) 将 \(\Phi_\alpha(0)\) 传播到 \(\Phi_\alpha(t)\) 来找到，对于 Floquet 模式，这会产生

\[U(t,0)\Phi_\alpha(0) = \exp(-i\epsilon_\alpha t/\hbar)\Phi_\alpha(t),\]

因此 \(\Phi_\alpha(t) = \exp(i\epsilon_\alpha t/\hbar) U(t,0)\Phi_\alpha(0)\)。由于 \(\Phi_\alpha(t)\) 是周期性的，我们只需要在 \(t \in [0, T]\) 范围内评估它，并且从 \(\Phi_\alpha(t \in [0,T])\) 我们可以直接评估任意大的 \(t\) 的 \(\Phi_\alpha(t)\)、\(\Psi_\alpha(t)\) 和 \(\Psi(t)\)。

QuTiP中的Floquet形式

QuTiP 提供了一系列函数来计算 Floquet 模式和准能量、Floquet 状态分解等，给定一个时间依赖的哈密顿量。

例如，考虑一个强驱动的两能级原子的情况，由哈密顿量描述

(5)\[ H(t) = -\frac{1}{2}\Delta\sigma_x - \frac{1}{2}\epsilon_0\sigma_z + \frac{1}{2}A\sin(\omega t)\sigma_z.\]

在QuTiP中，我们可以如下定义这个哈密顿量：

>>> delta = 0.2 * 2*np.pi
>>> eps0 = 1.0 * 2*np.pi
>>> A = 2.5 * 2*np.pi
>>> omega = 1.0 * 2*np.pi
>>> H0 = - delta/2.0 * sigmax() - eps0/2.0 * sigmaz()
>>> H1 = A/2.0 * sigmaz()
>>> args = {'w': omega}
>>> H = [H0, [H1, 'sin(w * t)']]

对应于哈密顿量 (5) 的 \(t=0\) Floquet 模式可以使用 FloquetBasis 类来计算，该类封装了 Floquet 模式和准能量：

>>> T = 2*np.pi / omega
>>> floquet_basis = FloquetBasis(H, T, args)
>>> f_energies = floquet_basis.e_quasi
>>> f_energies 
array([-2.83131212,  2.83131212])
>>> f_modes_0 = floquet_basis.mode(0)
>>> f_modes_0 
[Quantum object: dims = [[2], [1]], shape = (2, 1), type = ket
Qobj data =
[[ 0.72964231+0.j      ]
 [-0.39993746+0.554682j]],
Quantum object: dims = [[2], [1]], shape = (2, 1), type = ket
Qobj data =
[[0.39993746+0.554682j]
 [0.72964231+0.j      ]]]

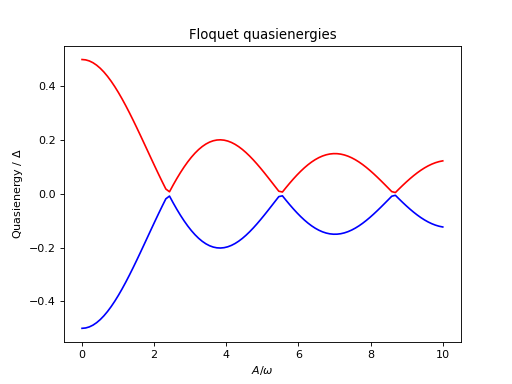
对于一些有趣的问题，仅从准能级就可以得出有趣的观察结果。例如，考虑上面介绍的驱动两能级系统的准能量作为驱动振幅的函数，在以下示例中计算并绘制。对于某些驱动振幅，准能级会交叉。由于准能量可以与长期动力学的时间尺度相关联，因此由于驱动，简并的准能量表明动力学的“冻结”（有时称为隧穿的相干破坏）。

>>> delta = 0.2 * 2 * np.pi
>>> eps0  = 0.0 * 2 * np.pi
>>> omega = 1.0 * 2 * np.pi
>>> A_vec = np.linspace(0, 10, 100) * omega
>>> T = (2 * np.pi) / omega
>>> tlist = np.linspace(0.0, 10 * T, 101)
>>> spsi0 = basis(2, 0)
>>> q_energies = np.zeros((len(A_vec), 2))
>>> H0 = delta / 2.0 * sigmaz() - eps0 / 2.0 * sigmax()
>>> args = {'w': omega}
>>> for idx, A in enumerate(A_vec): 
>>>   H1 = A / 2.0 * sigmax() 
>>>   H = [H0, [H1, lambda t, args: np.sin(args['w'] * t)]] 
>>>   floquet_basis = FloquetBasis(H, T, args)
>>>   q_energies[idx,:] = floquet_basis.e_quasi 
>>> plt.figure() 
>>> plt.plot(A_vec/omega, q_energies[:,0] / delta, 'b', A_vec/omega, q_energies[:,1] / delta, 'r') 
>>> plt.xlabel(r'$A/\omega$') 
>>> plt.ylabel(r'Quasienergy / $\Delta$') 
>>> plt.title(r'Floquet quasienergies') 
>>> plt.show() 

给定在 \(t=0\) 时的 Floquet 模式，我们使用 FloquetBasis.mode 来获取稍后时间 \(t\) 的 Floquet 模式：

>>> f_modes_t = floquet_basis.mode(2.5)
>>> f_modes_t 
[Quantum object: dims = [[2], [1]], shape = (2, 1), type = ket
Qobj data =
[[-0.89630512-0.23191946j]
 [ 0.37793106-0.00431336j]],
Quantum object: dims = [[2], [1]], shape = (2, 1), type = ket
Qobj data =
[[-0.37793106-0.00431336j]
 [-0.89630512+0.23191946j]]]

计算Floquet模式的目的是找到给定初始状态\(\left|\psi_0\right>\)的原始问题的波函数解(5)。为此，我们首先需要使用函数FloquetBasis.to_floquet_basis将初始状态分解为Floquet状态。

>>> psi0 = rand_ket(2)
>>> f_coeff = floquet_basis.to_floquet_basis(psi0)
>>> f_coeff 
[(-0.645265993068382+0.7304552549315746j),
(0.15517002114250228-0.1612116102238258j)]

并且给定初始状态在Floquet状态中的这种分解，我们可以轻松地评估波函数，这是(5)的解，在任意时间\(t\)使用函数FloquetBasis.from_floquet_basis:

>>> t = 10 * np.random.rand()
>>> psi_t = floquet_basis.from_floquet_basis(f_coeff, t)

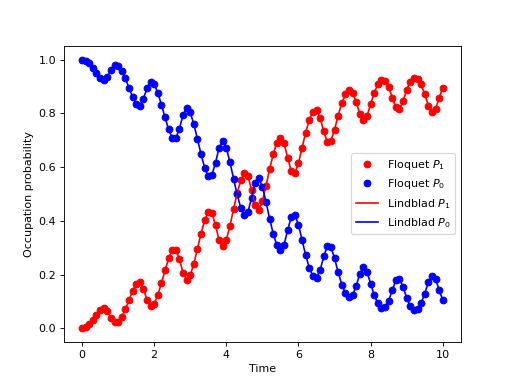
以下示例说明了如何使用上述函数来计算和绘制(5)的时间演化。

import numpy as np
from matplotlib import pyplot

import qutip

delta = 0.2 * 2*np.pi
eps0  = 1.0 * 2*np.pi
A     = 0.5 * 2*np.pi
omega = 1.0 * 2*np.pi
T      = (2*np.pi)/omega
tlist  = np.linspace(0.0, 10 * T, 101)
psi0   = qutip.basis(2, 0)

H0 = - delta/2.0 * qutip.sigmax() - eps0/2.0 * qutip.sigmaz()
H1 = A/2.0 * qutip.sigmaz()
args = {'w': omega}
H = [H0, [H1, lambda t, w: np.sin(w * t)]]

# Create the floquet system for the time-dependent hamiltonian
floquetbasis = qutip.FloquetBasis(H, T, args)

# decompose the inital state in the floquet modes
f_coeff = floquetbasis.to_floquet_basis(psi0)

# calculate the wavefunctions using the from the floquet modes coefficients
p_ex = np.zeros(len(tlist))
for n, t in enumerate(tlist):
    psi_t = floquetbasis.from_floquet_basis(f_coeff, t)
    p_ex[n] = qutip.expect(qutip.num(2), psi_t)

# For reference: calculate the same thing with mesolve
p_ex_ref = qutip.mesolve(H, psi0, tlist, e_ops=[qutip.num(2)], args=args).expect[0]

# plot the results
pyplot.plot(tlist, np.real(p_ex),     'ro', tlist, 1-np.real(p_ex),     'bo')
pyplot.plot(tlist, np.real(p_ex_ref), 'r',  tlist, 1-np.real(p_ex_ref), 'b')
pyplot.xlabel('Time')
pyplot.ylabel('Occupation probability')
pyplot.legend(("Floquet $P_1$", "Floquet $P_0$", "Lindblad $P_1$", "Lindblad $P_0$"))
pyplot.show()

预计算一个周期的Floquet模式

在评估Floquet状态或波函数在多个时间点时，预先计算驱动第一周期的Floquet模式与所需时间是非常有用的。可以传递要预先计算模式的时间列表给FloquetBasis，使用precompute=tlist，然后可以使用FloquetBasis.from_floquet_basis和FloquetBasis.to_floquet_basis来高效地检索预先计算的时间点的波函数。以下示例说明了如何使用这些函数预先计算Floquet模式，从而更高效地解决上一节中的示例：

import numpy as np
from matplotlib import pyplot
import qutip

delta = 0.0  * 2*np.pi
eps0  = 1.0 * 2*np.pi
A     = 0.25 * 2*np.pi
omega = 1.0 * 2*np.pi
T      = 2*np.pi / omega
tlist  = np.linspace(0.0, 10 * T, 101)
psi0   = qutip.basis(2,0)

H0 = - delta/2.0 * qutip.sigmax() - eps0/2.0 * qutip.sigmaz()
H1 = A/2.0 * qutip.sigmax()
args = {'w': omega}
H = [H0, [H1, lambda t, w: np.sin(w * t)]]

# find the floquet modes for the time-dependent hamiltonian
floquetbasis = qutip.FloquetBasis(H, T, args, precompute=tlist)

# decompose the inital state in the floquet modes
f_coeff = floquetbasis.to_floquet_basis(psi0)

# calculate the wavefunctions using the from the floquet modes coefficients
p_ex = np.zeros(len(tlist))
for n, t in enumerate(tlist):
    psi_t = floquetbasis.from_floquet_basis(f_coeff, t)
    p_ex[n] = qutip.expect(qutip.num(2), psi_t)

# For reference: calculate the same thing with mesolve
p_ex_ref = qutip.mesolve(H, psi0, tlist, e_ops=[qutip.num(2)], args=args).expect[0]

# plot the results
pyplot.plot(tlist, np.real(p_ex),     'ro', tlist, 1-np.real(p_ex),     'bo')
pyplot.plot(tlist, np.real(p_ex_ref), 'r',  tlist, 1-np.real(p_ex_ref), 'b')
pyplot.xlabel('Time')
pyplot.ylabel('Occupation probability')
pyplot.legend(("Floquet $P_1$", "Floquet $P_0$", "Lindblad $P_1$", "Lindblad $P_0$"))
pyplot.show()

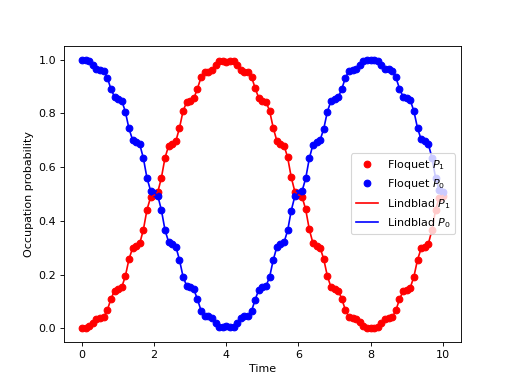
请注意，本示例中使用的参数和哈密顿量与上一节不同，因此生成的图表外观也有所不同。

为了方便起见，上述所有使用Floquet形式计算量子系统演化的步骤都被封装在函数fsesolve中。使用这个函数，我们可以像上面的例子一样得到相同的结果。

output = fsesolve(H, psi0=psi0, tlist=tlist, e_ops=[qutip.num(2)], args=args)
p_ex = output.expect[0]

耗散演化的Floquet理论

一个与其环境相互作用的驱动系统不一定能很好地用标准的Lindblad主方程来描述，因为其耗散过程可能由于驱动而随时间变化。在这种情况下，一种严格的方法是在推导主方程时考虑驱动。这可以通过许多不同的方式来完成，但一种常见的方法是在Floquet基中推导主方程。这种方法导致了所谓的Floquet-Markov主方程，详见Grifoni等人，Physics Reports 304, 299 (1998)。

为了简要概述推导过程，下面列出了在QuTiP中实现的重要内容。

Floquet模式 \(\ket{\phi_\alpha(t)}\) 指的是一类由 \(\epsilon_\alpha + k \Omega\) 定义的准能量，其中 \(k\) 是任意的。因此，两个Floquet模式之间的准能量差由以下公式给出：

\[\Delta_{\alpha \beta k} = \frac{\epsilon_\alpha - \epsilon_\beta}{\hbar} + k \Omega\]

对于任何耦合运算符 \(q\)（由用户提供），在Floquet基中的矩阵元素计算如下：

\[X_{\alpha \beta k} = \frac{1}{T} \int_0^T dt \; e^{-ik \Omega t} \bra{\phi_\alpha(t)}q\ket{\phi_\beta(t)}\]

从矩阵元素和谱密度 \(J(\omega)\) 中，定义了衰减率 \(\gamma_{\alpha \beta k}\)：

\[\gamma_{\alpha \beta k} = 2 \pi J(\Delta_{\alpha \beta k}) | X_{\alpha \beta k}|^2\]

主方程通过RWA进一步简化，这使得以下矩阵变得有用：

\[A_{\alpha \beta} = \sum_{k = -\infty}^\infty [\gamma_{\alpha \beta k} + n_{th}(|\Delta_{\alpha \beta k}|)(\gamma_{\alpha \beta k} + \gamma_{\alpha \beta -k})\]

系统的密度矩阵随后根据以下公式演化：

\[\dot{\rho}_{\alpha \alpha}(t) = \sum_\nu (A_{\alpha \nu} \rho_{\nu \nu}(t) - A_{\nu \alpha} \rho_{\alpha \alpha} (t))\]

\[\dot{\rho}_{\alpha \beta}(t) = -\frac{1}{2} \sum_\nu (A_{\nu \alpha} + A_{\nu \beta}) \rho_{\alpha \beta}(t) \qquad \alpha \neq \beta\]

QuTiP中的Floquet-Markov主方程

QuTiP函数fmmesolve实现了Floquet-Markov主方程。 它计算给定初始状态、时间依赖的哈密顿量、系统通过其耦合到环境的操作符列表以及描述环境的相应谱密度函数列表的系统的动力学。 与mesolve和mcsolve不同，fmmesolve并不用耗散率来表征环境，而是从噪声谱密度函数和瞬时哈密顿量参数中提取与环境的耦合强度（类似于Bloch-Redfield主方程求解器brmesolve）。

注意

目前，fmmesolve 只能接受单个环境耦合算子和谱密度函数。

环境的噪声谱密度函数被实现为一个Python回调函数，该函数被传递给求解器。例如：

gamma1 = 0.1
def noise_spectrum(omega):
    return (omega>0) * 0.5 * gamma1 * omega/(2*pi)

其他参数与mesolve和mcsolve类似， 并且使用相同的返回值格式Result。 以下示例扩展了上面研究的示例，并使用fmmesolve 将耗散引入计算中。

import numpy as np
from matplotlib import pyplot
import qutip

delta = 0.0  * 2*np.pi
eps0  = 1.0 * 2*np.pi
A     = 0.25 * 2*np.pi
omega = 1.0 * 2*np.pi
T      = 2*np.pi / omega
tlist  = np.linspace(0.0, 20 * T, 301)
psi0   = qutip.basis(2,0)

H0 = - delta/2.0 * qutip.sigmax() - eps0/2.0 * qutip.sigmaz()
H1 = A/2.0 * qutip.sigmax()
args = {'w': omega}
H = [H0, [H1, lambda t, w: np.sin(w * t)]]

# noise power spectrum
gamma1 = 0.1
def noise_spectrum(omega):
    return (omega>0) * 0.5 * gamma1 * omega/(2*np.pi)

# solve the floquet-markov master equation
output = qutip.fmmesolve(
    H, psi0, tlist, [qutip.sigmax()],
    spectra_cb=[noise_spectrum], T=T,
    args=args, options={"store_floquet_states": True}
)

# calculate expectation values in the computational basis
p_ex = np.zeros(tlist.shape, dtype=np.complex128)
for idx, t in enumerate(tlist):
    f_coeff_t = output.floquet_states[idx]
    psi_t = output.floquet_basis.from_floquet_basis(f_coeff_t, t)
    # Alternatively
    psi_t = output.states[idx]
    p_ex[idx] = qutip.expect(qutip.num(2), psi_t)

# For reference: calculate the same thing with mesolve
output = qutip.mesolve(
    H, psi0, tlist, [np.sqrt(gamma1) * qutip.sigmax()],
    e_ops=[qutip.num(2)], args=args
)
p_ex_ref = output.expect[0]

# plot the results
pyplot.plot(tlist, np.real(p_ex), 'r--', tlist, 1-np.real(p_ex), 'b--')
pyplot.plot(tlist, np.real(p_ex_ref), 'r', tlist, 1-np.real(p_ex_ref), 'b')
pyplot.xlabel('Time')
pyplot.ylabel('Occupation probability')
pyplot.legend(("Floquet $P_1$", "Floquet $P_0$", "Lindblad $P_1$", "Lindblad $P_0$"))
pyplot.show()

最后，fmmesolve 总是期望 e_ops 在实验室基础上指定（与其他求解器一样），我们可以使用以下方式计算期望值：

output = fmmesolve(H, psi0, tlist, [sigmax()], e_ops=[num(2)],
                   spectra_cb=[noise_spectrum], T=T, args=args)
p_ex = output.expect[0]