Lindblad主方程求解器
单一演化
封闭(纯)量子系统的动力学由薛定谔方程控制
其中 \(\Psi\) 是波函数,\(\hat H\) 是哈密顿量,\(\hbar\) 是普朗克常数。一般来说,薛定谔方程是一个偏微分方程(PDE),其中 \(\Psi\) 和 \(\hat H\) 都是空间和时间的函数。为了计算目的,将PDE展开在一组基函数中,这些基函数跨越哈密顿量的希尔伯特空间,并将方程写成矩阵和向量形式是有用的。
其中 \(\left|\psi\right>\) 是状态向量,\(H\) 是哈密顿量的矩阵表示。原则上,这个矩阵方程可以通过对角化哈密顿矩阵 \(H\) 来求解。然而,在实践中,除非希尔伯特空间的大小(矩阵 \(H\) 的维度)很小,否则很难执行这种对角化。从解析的角度来看,计算具有两个以上状态的系统的动力学是一项艰巨的任务。此外,如果我们考虑到由于与周围环境的不可避免的相互作用而导致的耗散,计算复杂性会变得更大,在所有现实情况下,我们不得不依赖于数值计算。这说明了数值计算在描述开放量子系统动力学中的重要性,以及为此任务需要高效且易于使用的工具。
薛定谔方程,它控制着封闭量子系统的时间演化,由其哈密顿量和状态向量定义。在前一节中,使用张量积和部分迹,我们展示了如何在QuTiP中构建哈密顿量和状态向量。给定一个哈密顿量,我们可以使用QuTiP求解器SESolver或函数sesolve计算任意状态向量\(\left|\psi_0\right>\)(psi0)的幺正(非耗散)时间演化。它通过使用常微分方程求解器,在时间列表times中的点上演化状态向量并评估一组运算符e_ops的期望值。
例如,计算一个初始处于上自旋状态的量子自旋-1/2系统的时间演化,隧道速率为0.1,并评估\(\sigma_z\)算符的期望值,使用以下代码
>>> H = 2*np.pi * 0.1 * sigmax()
>>> psi0 = basis(2, 0)
>>> times = np.linspace(0.0, 10.0, 20)
>>> solver = SESolver(H)
>>> result = solver.run(psi0, times, e_ops=[sigmaz()])
>>> result.expect
[array([ 1. , 0.78914057, 0.24548543, -0.40169579, -0.87947417,
-0.98636112, -0.67728018, -0.08257665, 0.54695111, 0.94581862,
0.94581574, 0.54694361, -0.08258559, -0.67728679, -0.9863626 ,
-0.87946979, -0.40168705, 0.24549517, 0.78914703, 1. ])]
请参阅下一节,了解使用mesolve进行耗散演化的示例。
该函数返回一个Result的实例,如前一节动力学模拟结果中所述。result中的属性expect是传递给e_ops参数的操作符的期望值列表。将多个操作符作为列表或字典传递给e_ops会为每个操作符生成一个期望值向量。result.e_data将期望值表示为期望输出列表的字典,而result.expect将这些值强制转换为numpy数组。
>>> solver.run(psi0, times, e_ops={"s_z": sigmaz(), "s_y": sigmay()}).e_data
{'s_z': [1.0, 0.7891405656865187, 0.24548542861367784, -0.40169578982499127,
..., 0.24549516882108563, 0.7891470300925004, 0.9999999999361128],
's_y': [0.0, -0.6142126403681064, -0.9694002807604085, -0.9157731664756708,
..., 0.9693978141534602, 0.6142043348073879, -1.1303742482923297e-05]}
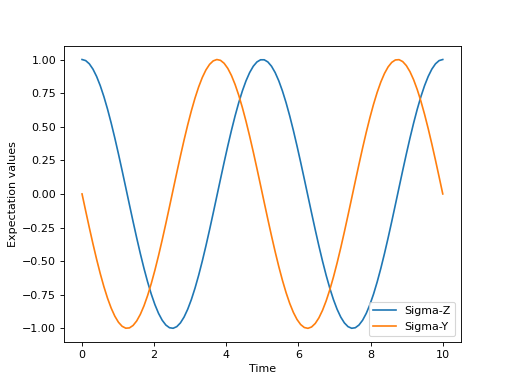
可以使用matplotlib的绘图函数轻松可视化得到的期望值:
>>> H = 2*np.pi * 0.1 * sigmax()
>>> psi0 = basis(2, 0)
>>> times = np.linspace(0.0, 10.0, 100)
>>> result = sesolve(H, psi0, times, e_ops=[sigmaz(), sigmay()])
>>> fig, ax = plt.subplots()
>>> ax.plot(result.times, result.expect[0])
>>> ax.plot(result.times, result.expect[1])
>>> ax.set_xlabel('Time')
>>> ax.set_ylabel('Expectation values')
>>> ax.legend(("Sigma-Z", "Sigma-Y"))
>>> plt.show()
如果将空的操作符列表传递给e_ops参数,sesolve和mesolve函数将返回一个Result实例,该实例包含在times中指定的时间点的状态向量列表。
>>> times = [0.0, 1.0]
>>> result = sesolve(H, psi0, times)
>>> result.states
[Quantum object: dims = [[2], [1]], shape = (2, 1), type = ket
Qobj data =
[[1.]
[0.]], Quantum object: dims = [[2], [1]], shape = (2, 1), type = ket
Qobj data =
[[0.80901699+0.j ]
[0. -0.58778526j]]]
非单一演化
虽然封闭量子系统中的状态向量的演化是确定性的,但开放量子系统本质上是随机的。环境对感兴趣的系统的影响是引起能级之间的随机跃迁,并在系统状态之间的相位差中引入不确定性。因此,开放量子系统的状态使用密度矩阵形式来描述,通过系综平均状态来描述。密度矩阵 \(\rho\) 描述了量子状态 \(\left|\psi_n\right>\) 的概率分布,在矩阵表示中 \(\rho = \sum_n p_n \left|\psi_n\right>\left<\psi_n\right|\),其中 \(p_n\) 是系统处于量子状态 \(\left|\psi_n\right>\) 的经典概率。密度矩阵 \(\rho\) 的时间演化是本部分剩余部分的主题。
林德布拉德主方程
推导系统与其环境相互作用的运动方程的标准方法是扩展系统的范围以包括环境。然后,组合的量子系统是封闭的,其演化由冯·诺伊曼方程控制。
相当于薛定谔方程 (1) 在密度矩阵形式中的表达。这里,总哈密顿量
包括原始系统的哈密顿量 \(H_{\rm sys}\),环境的哈密顿量 \(H_{\rm env}\),以及表示系统与其环境之间相互作用的项 \(H_{\rm int}\)。由于我们只对系统的动力学感兴趣,此时我们可以对公式 (2) 中的环境自由度进行部分迹运算,从而得到原始系统密度矩阵运动的主方程。这种演化的最一般迹保持且完全正的形式是约化密度矩阵 \(\rho = {\rm Tr}_{\rm env}[\rho_{\rm tot}]\) 的Lindblad主方程。
其中 \(C_n = \sqrt{\gamma_n} A_n\) 是坍缩算子,而 \(A_n\) 是环境通过 \(H_{\rm int}\) 与系统耦合的算子,\(\gamma_n\) 是对应的速率。 方程 (3) 的推导可以在多个来源中找到,这里不再重复。相反,我们强调从物理论证出发,得到方程 (3) 形式的主方程所需的近似,并因此在 QuTiP 中进行计算:
可分离性: 在 \(t=0\) 时,系统与其环境之间没有相关性,因此总密度矩阵可以写为张量积 \(\rho^I_{\rm tot}(0) = \rho^I(0) \otimes \rho^I_{\rm env}(0)\)。
玻恩近似: 需要满足以下条件:(1) 环境的状态不会因为与系统的相互作用而发生显著变化;(2) 系统和环境在整个演化过程中保持可分离性。如果相互作用较弱,并且环境比系统大得多,这些假设是合理的。总结来说,\(\rho_{\rm tot}(t) \approx \rho(t)\otimes\rho_{\rm env}\)。
马尔可夫近似 环境衰减的时间尺度 \(\tau_{\rm env}\) 远小于系统动力学的最小时间尺度 \(\tau_{\rm sys} \gg \tau_{\rm env}\)。这种近似 通常被称为“短记忆环境”,因为它要求环境相关函数在比系统更快的时间尺度上衰减。
长期近似 规定主方程中对应于跃迁频率的元素满足 \(|\omega_{ab}-\omega_{cd}| \ll 1/\tau_{\rm sys}\),即所有在相互作用图像中的快速旋转项都可以忽略。它也忽略了导致系统能级微小重整化的项。这种近似并非对所有主方程形式都是严格必要的(例如,Block-Redfield主方程),但为了达到Lindblad形式 (3),这是必需的,该形式用于
mesolve。
对于满足上述条件的系统环境,Lindblad主方程(3)控制着系统密度矩阵的时间演化,给出了系统动力学的整体平均值。为了确保这些近似不被违反,重要的是衰减率\(\gamma_n\)要小于系统哈密顿量中的最小能量分裂。因此,需要特别注意的情况包括,例如,与环境强耦合的系统,以及具有退化或接近退化能级的系统。
对于量子系统的非幺正演化,即包括诸如弛豫和退相干等非相干过程的演化,通常使用主方程。在QuTiP中,函数mesolve用于两种情况:根据薛定谔方程的演化和根据主方程的演化,尽管这两种运动方程非常不同。mesolve函数会自动确定是否足以使用薛定谔方程(如果没有给出崩溃算符)或者是否必须使用主方程(如果给出了崩溃算符)。请注意,根据薛定谔方程计算时间演化比使用主方程更容易且更快(对于大系统),因此如果可能,求解器将回退到使用薛定谔方程。
与薛定谔方程相比,主方程中的新内容是描述量子系统由于与环境相互作用而导致的耗散过程。这些环境相互作用由系统与环境耦合的算子以及描述过程强度的速率定义。
在QuTiP中,速率的平方根与描述耗散过程的算符的乘积被称为坍缩算符。坍缩算符的列表(c_ops)作为第四个参数传递给mesolve函数,以在主方程中定义耗散过程。当c_ops不为空时,mesolve函数将使用主方程而不是幺正的薛定谔方程。
使用上一节中的自旋动力学示例,我们可以通过在mesolve函数的第四个参数中添加np.sqrt(0.05) * sigmax()来轻松添加一个弛豫过程(描述自旋能量耗散到其环境中的过程)。
>>> times = np.linspace(0.0, 10.0, 100)
>>> result = mesolve(H, psi0, times, [np.sqrt(0.05) * sigmax()], e_ops=[sigmaz(), sigmay()])
>>> fig, ax = plt.subplots()
>>> ax.plot(times, result.expect[0])
>>> ax.plot(times, result.expect[1])
>>> ax.set_xlabel('Time')
>>> ax.set_ylabel('Expectation values')
>>> ax.legend(("Sigma-Z", "Sigma-Y"))
>>> plt.show()
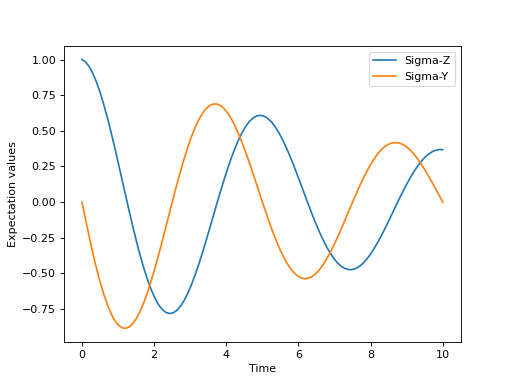
这里,0.05 是速率,运算符 \(\sigma_x\) (sigmax)
描述了耗散过程。
现在来看一个稍微复杂一点的例子:考虑一个通过偶极型相互作用与泄漏单模腔耦合的两能级原子,这种相互作用支持两个系统之间的量子相干交换。如果原子最初处于基态,而腔处于5光子福克态,则使用以下代码行计算动力学。
>>> times = np.linspace(0.0, 10.0, 200)
>>> psi0 = tensor(fock(2,0), fock(10, 5))
>>> a = tensor(qeye(2), destroy(10))
>>> sm = tensor(destroy(2), qeye(10))
>>> H = 2 * np.pi * a.dag() * a + 2 * np.pi * sm.dag() * sm + 2 * np.pi * 0.25 * (sm * a.dag() + sm.dag() * a)
>>> result = mesolve(H, psi0, times, [np.sqrt(0.1)*a], e_ops=[a.dag()*a, sm.dag()*sm])
>>> plt.figure()
>>> plt.plot(times, result.expect[0])
>>> plt.plot(times, result.expect[1])
>>> plt.xlabel('Time')
>>> plt.ylabel('Expectation values')
>>> plt.legend(("cavity photon number", "atom excitation probability"))
>>> plt.show()
