解决时间依赖哈密顿量的问题

时间依赖运算符

在之前的量子演化示例中，我们假设所考虑的系统由时间无关的哈密顿量描述。然而，许多系统在哈密顿量或描述与环境耦合的坍缩算子中具有显式的时间依赖性，有时这两个组件都可能依赖于时间。时间演化求解器如sesolve、brmesolve等都能够处理时间依赖的哈密顿量和坍缩项。QuTiP使用QobjEvo来表示时间依赖的量子算子。构建QobjEvo有三种不同的方式：

1. 基于函数的: 从返回Qobj的函数构建时间依赖的运算符:

def oper(t):
    return num(N) + (destroy(N) + create(N)) * np.sin(t)

H_t = QobjEvo(oper)

1. 基于列表：时间相关的量子算子表示为qobj和[qobj, coefficient]对的列表：

H_t = QobjEvo([num(N), [create(N), lambda t: np.sin(t)], [destroy(N), lambda t: np.sin(t)]])

3. 基于系数的：一个Qobj与一个Coefficient的乘积，由coefficient函数创建，结果为一个QobjEvo：

coeff = coefficent(lambda t: np.sin(t))
H_t = num(N) + (destroy(N) + create(N)) * coeff

这三个示例将创建相同的时间依赖算子，然而在求解器中使用基于函数的方法通常会较慢。

大多数求解器在需要操作符时接受QobjEvo：这包括哈密顿量H、崩溃操作符、期望值操作符、brmesolve的a_ops操作符等。例外是krylovsolve的哈密顿量和HEOM的浴操作符。

大多数求解器将接受任何可以转换为QobjEvo的哈密顿量格式。 以下所有内容都是等效的：

result = mesolve(H_t, ...)
result = mesolve([num(N), [destroy(N) + create(N), lambda t: np.sin(t)]], ...)
result = mesolve(oper, ...)

Collapse 操作符也接受可以转换为 QobjEvo 的对象列表。 然而，需要注意不要将 c_ops 参数的列表性质与列表格式的量子系统混淆。在以下调用中：

result = mesolve(H_t, ..., c_ops=[num(N), [destroy(N) + create(N), lambda t: np.sin(t)]])

mesolve 将会看到两个崩溃操作符： num(N) 和 [destroy(N) + create(N), lambda t: np.sin(t)]。 因此，建议将每个崩溃操作符作为 Qobj 或 QobjEvo 传递。

作为一个例子，我们将研究一个具有时间依赖哈密顿量的情况，其形式为 \(H=H_{0}+f(t)H_{1}\)，其中 \(f(t)\) 是时间依赖的驱动强度， 给定为 \(f(t)=A\exp\left[-\left( t/\sigma \right)^{2}\right]\)。 以下代码设置了这个问题

ustate = basis(3, 0)
excited = basis(3, 1)
ground = basis(3, 2)

N = 2 # Set where to truncate Fock state for cavity
sigma_ge = tensor(qeye(N), ground * excited.dag())  # |g><e|
sigma_ue = tensor(qeye(N), ustate * excited.dag())  # |u><e|
a = tensor(destroy(N), qeye(3))
ada = tensor(num(N), qeye(3))

c_ops = []  # Build collapse operators
kappa = 1.5 # Cavity decay rate
c_ops.append(np.sqrt(kappa) * a)
gamma = 6  # Atomic decay rate
c_ops.append(np.sqrt(5*gamma/9) * sigma_ue) # Use Rb branching ratio of 5/9 e->u
c_ops.append(np.sqrt(4*gamma/9) * sigma_ge) # 4/9 e->g

t = np.linspace(-15, 15, 100) # Define time vector
psi0 = tensor(basis(N, 0), ustate) # Define initial state

state_GG = tensor(basis(N, 1), ground) # Define states onto which to project
sigma_GG = state_GG * state_GG.dag()
state_UU = tensor(basis(N, 0), ustate)
sigma_UU = state_UU * state_UU.dag()

g = 5  # coupling strength
H0 = -g * (sigma_ge.dag() * a + a.dag() * sigma_ge)  # time-independent term
H1 = (sigma_ue.dag() + sigma_ue)  # time-dependent term

鉴于我们有一个单一的时间依赖哈密顿项和恒定的坍缩项，我们需要为系数\(f(t)\)指定一个Python函数。在这种情况下，可以简单地这样做

def H1_coeff(t):
    return 9 * np.exp(-(t / 5.) ** 2)

在这种情况下，返回值仅取决于时间。然而，可以向调用中添加可选参数，请参阅使用参数。指定了我们的系数函数后，我们现在可以以列表格式指定哈密顿量并调用求解器（在这种情况下是mesolve）

H = [H0, [H1, H1_coeff]]
output = mesolve(H, psi0, t, c_ops, e_ops=[ada, sigma_UU, sigma_GG])

我们可以以完全相同的方式调用蒙特卡洛求解器（如果使用默认的ntraj=500）：

output = mcsolve(H, psi0, t, c_ops, e_ops=[ada, sigma_UU, sigma_GG])

主方程求解器的输出与示例中显示的相同，然而蒙特卡罗方法的结果将明显偏离，这表明我们应该增加这个示例的轨迹数量。此外，我们还可以考虑具有时变衰减率的简单谐振子的衰减。

kappa = 0.5

def col_coeff(t, args):  # coefficient function
    return np.sqrt(kappa * np.exp(-t))

N = 10  # number of basis states
a = destroy(N)
H = a.dag() * a  # simple HO
psi0 = basis(N, 9)  # initial state
c_ops = [QobjEvo([a, col_coeff])]  # time-dependent collapse term
times = np.linspace(0, 10, 100)
output = mesolve(H, psi0, times, c_ops, e_ops=[a.dag() * a])

Qobjevo

QobjEvo 作为一个时间依赖的量子系统，其主要功能是在某个时间点创建一个 Qobj：

>>> print(H_t(np.pi / 2))
Quantum object: dims=[[2], [2]], shape=(2, 2), type='oper', isherm=True
Qobj data =
[[0. 1.]
 [1. 1.]]

QobjEvo 与 Qobj 有许多共同属性。

属性	特性	描述
维度	Q.dims	塑造张量结构。
形状	Q.shape	基础数据矩阵的维度。
类型	Q.type	对象是‘ket’、‘bra’、‘oper’还是‘super’类型？
表示	Q.superrep	如果type是'super'时使用的表示？
是常数	Q.isconstant	QobjEvo 是否依赖于时间。

QobjEvo 遵循与 Qobj 相同的数学运算规则。 它们可以与标量、Qobj 和 QobjEvo 进行加、减和乘运算。 它们还支持 dag、trans 和 conj 方法，并且可以用于张量运算和超算符变换：

H = tensor(H_t, qeye(2))
c_op = tensor(QobjEvo([destroy(N), lambda t: np.exp(-t)]), sigmax())

L = -1j * (spre(H) - spost(H.dag()))
L += spre(c_op) * spost(c_op.dag()) - 0.5 * spre(c_op.dag() * c_op) - 0.5 * spost(c_op.dag() * c_op)

或者等价地：

L = liouvillian(H, [c_op])

使用参数

到目前为止，系数仅是时间的函数。在H1_coeff的定义中，驱动幅度A和宽度sigma被硬编码为它们的数值。这对于专门的问题或我们只想运行一次的问题来说是可以的。然而，在许多情况下，我们希望使用一系列参数来研究相同的问题，而不必担心每次运行时手动更改值。QuTiP允许您通过向系数函数添加额外的参数来实现这一点，这些参数使QobjEvo。例如，我们可以添加一个args位置变量，而不是明确地写出高斯驱动项的幅度为9和宽度为5：

>>> def H1_coeff(t, args):
>>>     return args['A'] * np.exp(-(t/args['sigma'])**2)

或者，从v5开始，直接添加额外的参数：

>>> def H1_coeff(t, A, sigma):
>>>     return A * np.exp(-(t / sigma)**2)

当系数函数的第二个位置输入被命名为 args 时， 参数会以 Python 字典的形式传递，字典中包含 key: value 对。 否则，系数函数会以 coeff(t, **args) 的形式调用。 在最后一个例子中，args = {'A': a, 'sigma': b}，其中 a 和 b 分别是 振幅和宽度的两个参数。 这个 args 字典需要在创建 QobjEvo 时提供，当 使用这些函数时：

>>> system = [sigmaz(), [sigmax(), H1_coeff]]
>>> args={'A': 9, 'sigma': 5}
>>> qevo = QobjEvo(system, args=args)

但没有args，QobjEvo的创建将会失败：

>>> QobjEvo(system)
TypeError: H1_coeff() missing 2 required positional arguments: 'A' and 'sigma'

在评估QobjEvo时，可以通过args字典位置参数或特定关键字参数传递新的参数：

>>> print(qevo(1))
Quantum object: dims=[[2], [2]], shape=(2, 2), type='oper', isherm=True
Qobj data =
[[ 1.          8.64710495]
 [ 8.64710495 -1.        ]]
>>> print(qevo(1, {"A": 5, "sigma": 0.2}))
Quantum object: dims=[[2], [2]], shape=(2, 2), type='oper', isherm=True
Qobj data =
[[ 1.00000000e+00  6.94397193e-11]
 [ 6.94397193e-11 -1.00000000e+00]]
>>> print(qevo(1, A=5))
Quantum object: dims=[[2], [2]], shape=(2, 2), type='oper', isherm=True
Qobj data =
[[ 1.         4.8039472]
 [ 4.8039472 -1.       ]]

原始系数是否使用了args或特定输入并不重要。混合不同的签名是可以的。

求解器调用需要一个args输入，用于构建时间依赖系统。 如果哈密顿量或崩溃算子已经是QobjEvo，它们的参数将被覆盖。

def system(t, A, sigma):
    return H0 + H1 * (A * np.exp(-(t / sigma)**2))

mesolve(system, ..., args=args)

要更新现有时间依赖量子系统的参数，您可以将前一个对象作为带有新args的QobjEvo的输入传递：

>>> new_qevo = QobjEvo(qevo, args={"A": 5, "sigma": 0.2})
>>> new_qevo(1) == qevo(1, {"A": 5, "sigma": 0.2})
True

QobjEvo 从单一函数创建的也可以使用参数：

def oper(t, w):
    return num(N) + (destroy(N) + create(N)) * np.sin(t*w)

H_t = QobjEvo(oper, args={"w": np.pi})

当合并两个或多个QobjEvo时，每个都将保留其参数，但使用更新的参数调用它将影响所有部分：

>>> qevo1 = QobjEvo([[sigmap(), lambda t, a: a]], args={"a": 1})
>>> qevo2 = QobjEvo([[sigmam(), lambda t, a: a]], args={"a": 2})
>>> summed_evo = qevo1 + qevo2
>>> print(summed_evo(0))
Quantum object: dims=[[2], [2]], shape=(2, 2), type='oper', isherm=False
Qobj data =
[[0. 1.]
 [2. 0.]]
>>> print(summed_evo(0, a=3, b=1))
Quantum object: dims=[[2], [2]], shape=(2, 2), type='oper', isherm=True
Qobj data =
[[0. 3.]
 [3. 0.]]

系数

为了构建时间依赖的量子系统，我们经常使用一系列Qobj和 Coefficient。这些Coefficient表示相应量子对象的强度，作为时间的函数。到目前为止，我们使用函数来表示这些，但QuTiP支持多种格式：callable、strings、array。

函数系数 : 使用具有签名 f(t: double, ...) -> double 的可调用对象作为系数。 任何可以通过 f(t, args), f(t, **args) 调用的函数或方法都被接受。

def coeff(t, A, sigma):
    return A * np.exp(-(t / sigma)**2)

H = QobjEvo([H0, [H1, coeff]], args=args)

字符串系数： 使用包含简单Python表达式的字符串。 变量t，常见的数学函数如sin或exp以及args中的变量将可用。如果可用，字符串将使用cython编译，尽可能固定变量类型，允许比函数稍快的执行速度。虽然速度提升通常非常小，但在长时间演化中，会多次调用函数，这可能会累积。从版本5开始，系数的编译只进行一次，并在会话之间保存。当cython或filelock模块不可用时，代码将在python中使用exec执行，使用相同的环境。然而，这并不比使用python函数有优势。

coeff = "A * exp(-(t / sigma)**2)"

H = QobjEvo([H0, [H1, coeff]], args=args)

Here is a list of defined variables:

sin, cos, tan, asin, acos, atan, pi, sinh, cosh, tanh, asinh, acosh, atanh, exp, log, log10, erf, zerf, sqrt, real, imag, conj, abs, norm, arg, proj, np (numpy), spe (scipy.special) 和 cython_special (scipy cython 接口).

数组系数： 使用数组的样条插值。 当系数难以定义为函数或从实验数据中获得时，这很有用。 定义数组的时间必须作为tlist传递：

times = np.linspace(-sigma*5, sigma*5, 500)
coeff = A * exp(-(times / sigma)**2)

H = QobjEvo([H0, [H1, coeff]], tlist=times)

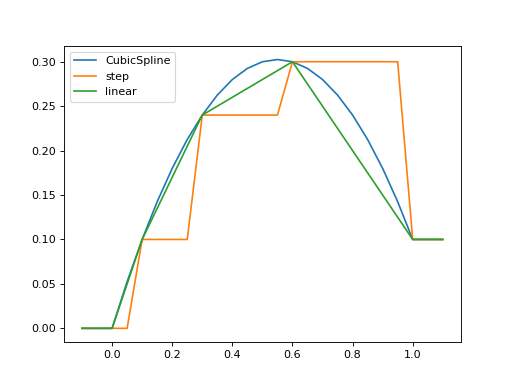
默认情况下，使用三次样条插值，但可以通过order输入控制插值的顺序： 在插值范围之外，使用第一个或最后一个值。

times = np.array([0, 0.1, 0.3, 0.6, 1.0])
coeff = times * (1.1 - times)
tlist = np.linspace(-0.1, 1.1, 25)

H = QobjEvo([qeye(1), coeff], tlist=times)
plt.plot(tlist, [H(t).norm() for t in tlist], label="CubicSpline")

H = QobjEvo([qeye(1), coeff], tlist=times, order=0)
plt.plot(tlist, [H(t).norm() for t in tlist], label="step")

H = QobjEvo([qeye(1), coeff], tlist=times, order=1)
plt.plot(tlist, [H(t).norm() for t in tlist], label="linear")

plt.legend()

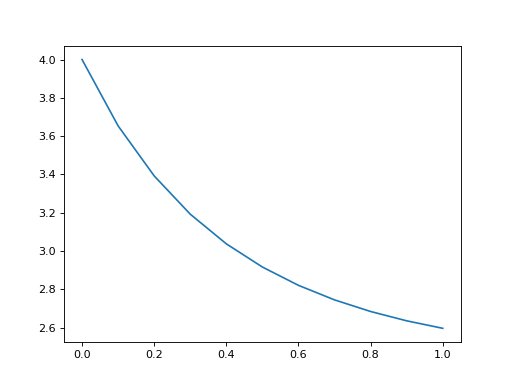
在求解器中使用数组系数时，如果时间相关的量子系统是列表格式，求解器的tlist将用作数组的时间。这通常并不理想，因为在范围的极端附近插值通常不太精确。因此，最好在求解器之前使用扩展范围创建QobjEvo：

N = 5
times = np.linspace(-0.1, 1.1, 13)
coeff = np.exp(-times)

c_ops = [QobjEvo([destroy(N), coeff], tlist=times)]
tlist = np.linspace(0, 1, 11)
data = mesolve(qeye(N), basis(N, N-1), tlist, c_ops=c_ops, e_ops=[num(N)]).expect[0]
plt.plot(tlist, data)

在QobjEvo中可以混合使用不同类型的系数。

鉴于输入风格的多种选择，首先出现的问题是选择哪个选项？ 简而言之，基于函数的方法（第一个选项）是最通用的， 允许通过用户定义的函数表达基本上任意的系数。 然而，通过自动将您的系统编译成C++代码， 基于字符串的选项（第二个选项）往往更高效且运行更快。 当然，对于较小的系统规模和演化时间，差异将很小。 最后，样条方法通常与字符串方法一样快，但一旦创建就无法修改。

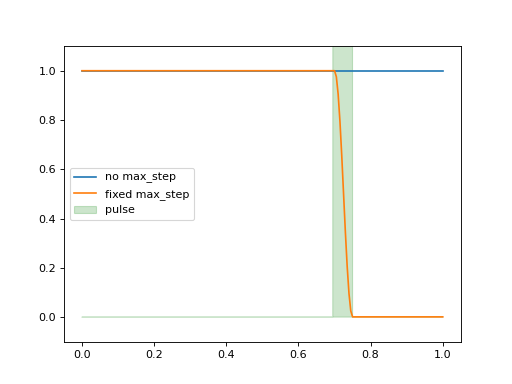
处理脉冲

在处理脉冲时需要特别小心。ODE求解器会自动选择步长，如果没有适当警告，可能会错过细小的脉冲。具有可变步长的积分方法有max_step选项，用于控制单个内部积分步长的最大值。此值应设置为小于脉冲宽度的一半，以确保不会错过它们。

例如，如果不固定最大步长，以下脉冲将被错过。

def pulse(t):
    return 10 * np.pi * (0.7 < t < 0.75)

tlist = np.linspace(0, 1, 201)
H = [sigmaz(), [sigmax(), pulse]]
psi0 = basis(2,1)

data1 = sesolve(H, psi0, tlist, e_ops=num(2)).expect[0]
data2 = sesolve(H, psi0, tlist, e_ops=num(2), options={"max_step": 0.01}).expect[0]

plt.plot(tlist, data1, label="no max_step")
plt.plot(tlist, data2, label="fixed max_step")
plt.fill_between(tlist, [pulse(t) for t in tlist], color="g", alpha=0.2, label="pulse")
plt.ylim([-0.1, 1.1])
plt.legend(loc="center left")