Note
Go to the end to download the full example code. or to run this example in your browser via Binder
时间序列预测的滞后特征#
本示例演示了如何使用Polars设计的滞后特征,通过
HistGradientBoostingRegressor 在自行车共享需求数据集上进行时间序列预测。
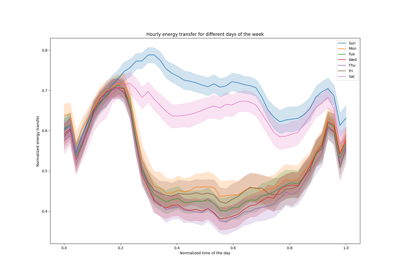
请参阅示例 时间相关特征工程 以了解该数据集的一些数据探索和周期性特征工程的演示。
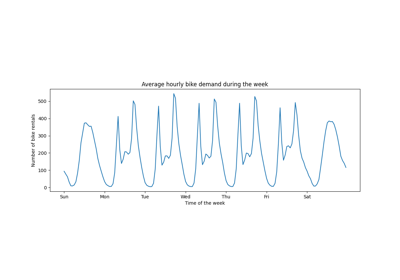
分析共享单车需求数据集#
我们首先从 OpenML 仓库加载数据为 pandas 数据框。一旦 fetch_openml 增加对 Polars 的原生支持,这将被替换为 Polars。我们转换为 Polars 进行特征工程,因为它会自动缓存在多个表达式中重用的常见子表达式(如下面的 pl.col("count").shift(1) )。更多信息请参见 https://docs.pola.rs/user-guide/lazy/optimizations/。
import numpy as np
import polars as pl
from sklearn.datasets import fetch_openml
pl.Config.set_fmt_str_lengths(20)
bike_sharing = fetch_openml(
"Bike_Sharing_Demand", version=2, as_frame=True, parser="pandas"
)
df = bike_sharing.frame
df = pl.DataFrame({col: df[col].to_numpy() for col in df.columns})
接下来,我们查看数据集的统计摘要,以便更好地理解我们正在处理的数据。
import polars.selectors as cs
summary = df.select(cs.numeric()).describe()
summary
让我们查看数据集中出现的季节 "fall" 、 "spring" 、 "summer" 和 "winter" 的计数,以确认它们是平衡的。
import matplotlib.pyplot as plt
df["season"].value_counts()
生成由Polars处理的滞后特征#
让我们考虑这样一个问题:根据过去的需求预测下一小时的需求。由于需求是一个连续变量,可以直观地使用任何回归模型。然而,我们没有通常的 (X_train, y_train) 数据集。相反,我们只有按时间顺序组织的 y_train 需求数据。
lagged_df = df.select(
"count",
*[pl.col("count").shift(i).alias(f"lagged_count_{i}h") for i in [1, 2, 3]],
lagged_count_1d=pl.col("count").shift(24),
lagged_count_1d_1h=pl.col("count").shift(24 + 1),
lagged_count_7d=pl.col("count").shift(7 * 24),
lagged_count_7d_1h=pl.col("count").shift(7 * 24 + 1),
lagged_mean_24h=pl.col("count").shift(1).rolling_mean(24),
lagged_max_24h=pl.col("count").shift(1).rolling_max(24),
lagged_min_24h=pl.col("count").shift(1).rolling_min(24),
lagged_mean_7d=pl.col("count").shift(1).rolling_mean(7 * 24),
lagged_max_7d=pl.col("count").shift(1).rolling_max(7 * 24),
lagged_min_7d=pl.col("count").shift(1).rolling_min(7 * 24),
)
lagged_df.tail(10)
请注意,前几行的值是未定义的,因为它们自身的过去是未知的。这取决于我们使用了多少滞后:
lagged_df.head(10)
我们现在可以将滞后特征分离到矩阵 X 中,并将目标变量(要预测的计数)分离到具有相同第一维度的数组 y 中。
lagged_df = lagged_df.drop_nulls()
X = lagged_df.drop("count")
y = lagged_df["count"]
print("X shape: {}\ny shape: {}".format(X.shape, y.shape))
X shape: (17210, 13)
y shape: (17210,)
朴素评估下一小时的自行车需求回归#
我们将随机拆分表格化的数据集,以训练梯度提升回归树(GBRT)模型,并使用平均绝对百分比误差(MAPE)进行评估。如果我们的模型旨在预测(即从过去数据预测未来数据),则不应使用晚于测试数据的训练数据。在时间序列机器学习中,“i.i.d”(独立同分布)假设不成立,因为数据点不是独立的,并且具有时间关系。
from sklearn.ensemble import HistGradientBoostingRegressor
from sklearn.model_selection import train_test_split
X_train, X_test, y_train, y_test = train_test_split(
X, y, test_size=0.2, random_state=42
)
model = HistGradientBoostingRegressor().fit(X_train, y_train)
查看模型的性能表现。
from sklearn.metrics import mean_absolute_percentage_error
y_pred = model.predict(X_test)
mean_absolute_percentage_error(y_test, y_pred)
np.float64(0.391498935135597)
适当的下一小时预测评估#
让我们使用适当的评估拆分策略,考虑数据集的时间结构来评估我们模型预测未来数据点的能力(避免通过读取训练集中滞后特征的值来作弊)。
from sklearn.model_selection import TimeSeriesSplit
ts_cv = TimeSeriesSplit(
n_splits=3, # to keep the notebook fast enough on common laptops
gap=48, # 2 days data gap between train and test
max_train_size=10000, # keep train sets of comparable sizes
test_size=3000, # for 2 or 3 digits of precision in scores
)
all_splits = list(ts_cv.split(X, y))
训练模型并基于MAPE评估其性能。
train_idx, test_idx = all_splits[0]
X_train, X_test = X[train_idx, :], X[test_idx, :]
y_train, y_test = y[train_idx], y[test_idx]
model = HistGradientBoostingRegressor().fit(X_train, y_train)
y_pred = model.predict(X_test)
mean_absolute_percentage_error(y_test, y_pred)
np.float64(0.44300751539296973)
通过打乱训练集和测试集来测量的泛化误差过于乐观。基于时间的分割方式进行泛化可能更能代表回归模型的真实性能。让我们通过适当的交叉验证来评估误差评估的这种变异性:
from sklearn.model_selection import cross_val_score
cv_mape_scores = -cross_val_score(
model, X, y, cv=ts_cv, scoring="neg_mean_absolute_percentage_error"
)
cv_mape_scores
array([0.44300752, 0.27772182, 0.3697178 ])
不同分割之间的变异性相当大!在实际情况下,建议使用更多的分割来更好地评估变异性。从现在开始,我们将报告平均交叉验证分数及其标准差。
print(f"CV MAPE: {cv_mape_scores.mean():.3f} ± {cv_mape_scores.std():.3f}")
CV MAPE: 0.363 ± 0.068
我们可以计算多种评估指标和损失函数的组合,结果会在稍后报告。
from collections import defaultdict
from sklearn.metrics import (
make_scorer,
mean_absolute_error,
mean_pinball_loss,
root_mean_squared_error,
)
from sklearn.model_selection import cross_validate
def consolidate_scores(cv_results, scores, metric):
if metric == "MAPE":
scores[metric].append(f"{value.mean():.2f} ± {value.std():.2f}")
else:
scores[metric].append(f"{value.mean():.1f} ± {value.std():.1f}")
return scores
scoring = {
"MAPE": make_scorer(mean_absolute_percentage_error),
"RMSE": make_scorer(root_mean_squared_error),
"MAE": make_scorer(mean_absolute_error),
"pinball_loss_05": make_scorer(mean_pinball_loss, alpha=0.05),
"pinball_loss_50": make_scorer(mean_pinball_loss, alpha=0.50),
"pinball_loss_95": make_scorer(mean_pinball_loss, alpha=0.95),
}
loss_functions = ["squared_error", "poisson", "absolute_error"]
scores = defaultdict(list)
for loss_func in loss_functions:
model = HistGradientBoostingRegressor(loss=loss_func)
cv_results = cross_validate(
model,
X,
y,
cv=ts_cv,
scoring=scoring,
n_jobs=2,
)
time = cv_results["fit_time"]
scores["loss"].append(loss_func)
scores["fit_time"].append(f"{time.mean():.2f} ± {time.std():.2f} s")
for key, value in cv_results.items():
if key.startswith("test_"):
metric = key.split("test_")[1]
scores = consolidate_scores(cv_results, scores, metric)
通过分位数回归建模预测不确定性#
与最小二乘法和泊松损失那样对 \(Y|X\) 的分布期望值进行建模不同,可以尝试估计条件分布的分位数。
\(Y|X=x_i\) 被认为是一个给定数据点 \(x_i\) 的随机变量,因为我们预计租赁数量无法从特征中100%准确预测。它可能会受到现有滞后特征未能充分捕捉的其他变量的影响。例如,未来一小时是否会下雨无法完全从过去几小时的自行车租赁数据中预测。这就是我们所说的偶然性不确定性。
分位数回归使得在不对分布形状做出强假设的情况下,可以更精细地描述该分布。
quantile_list = [0.05, 0.5, 0.95]
for quantile in quantile_list:
model = HistGradientBoostingRegressor(loss="quantile", quantile=quantile)
cv_results = cross_validate(
model,
X,
y,
cv=ts_cv,
scoring=scoring,
n_jobs=2,
)
time = cv_results["fit_time"]
scores["fit_time"].append(f"{time.mean():.2f} ± {time.std():.2f} s")
scores["loss"].append(f"quantile {int(quantile*100)}")
for key, value in cv_results.items():
if key.startswith("test_"):
metric = key.split("test_")[1]
scores = consolidate_scores(cv_results, scores, metric)
scores_df = pl.DataFrame(scores)
scores_df
让我们看看最小化每个指标的损失。
def min_arg(col):
col_split = pl.col(col).str.split(" ")
return pl.arg_sort_by(
col_split.list.get(0).cast(pl.Float64),
col_split.list.get(2).cast(pl.Float64),
).first()
scores_df.select(
pl.col("loss").get(min_arg(col_name)).alias(col_name)
for col_name in scores_df.columns
if col_name != "loss"
)
即使由于数据集的方差导致得分分布重叠, loss="squared_error" 时的平均 RMSE 仍然较低,而 loss="absolute_error" 时的平均 MAPE 也如预期般较低。对于 5 和 95 分位数的平均 Pinball Loss 也是如此。对应于 50 分位数损失的得分与通过最小化其他损失函数获得的得分重叠,MAE 也是这种情况。
对预测结果的定性观察#
我们现在可以通过可视化来观察模型在第5百分位数、中位数和第95百分位数上的表现:
all_splits = list(ts_cv.split(X, y))
train_idx, test_idx = all_splits[0]
X_train, X_test = X[train_idx, :], X[test_idx, :]
y_train, y_test = y[train_idx], y[test_idx]
max_iter = 50
gbrt_mean_poisson = HistGradientBoostingRegressor(loss="poisson", max_iter=max_iter)
gbrt_mean_poisson.fit(X_train, y_train)
mean_predictions = gbrt_mean_poisson.predict(X_test)
gbrt_median = HistGradientBoostingRegressor(
loss="quantile", quantile=0.5, max_iter=max_iter
)
gbrt_median.fit(X_train, y_train)
median_predictions = gbrt_median.predict(X_test)
gbrt_percentile_5 = HistGradientBoostingRegressor(
loss="quantile", quantile=0.05, max_iter=max_iter
)
gbrt_percentile_5.fit(X_train, y_train)
percentile_5_predictions = gbrt_percentile_5.predict(X_test)
gbrt_percentile_95 = HistGradientBoostingRegressor(
loss="quantile", quantile=0.95, max_iter=max_iter
)
gbrt_percentile_95.fit(X_train, y_train)
percentile_95_predictions = gbrt_percentile_95.predict(X_test)
我们现在可以看看回归模型所做的预测:
last_hours = slice(-96, None)
fig, ax = plt.subplots(figsize=(15, 7))
plt.title("Predictions by regression models")
ax.plot(
y_test[last_hours],
"x-",
alpha=0.2,
label="Actual demand",
color="black",
)
ax.plot(
median_predictions[last_hours],
"^-",
label="GBRT median",
)
ax.plot(
mean_predictions[last_hours],
"x-",
label="GBRT mean (Poisson)",
)
ax.fill_between(
np.arange(96),
percentile_5_predictions[last_hours],
percentile_95_predictions[last_hours],
alpha=0.3,
label="GBRT 90% interval",
)
_ = ax.legend()
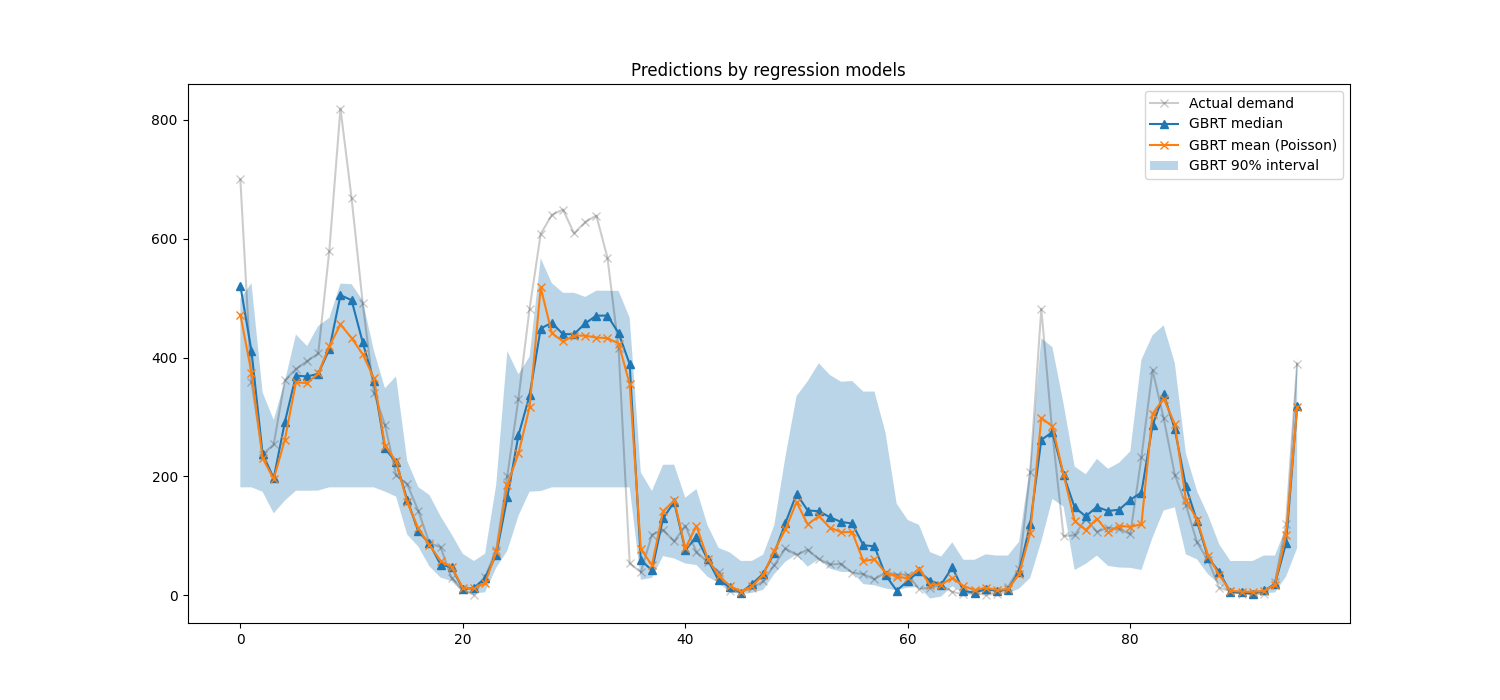
这里有趣的是注意到5%和95%百分位估计值之间的蓝色区域宽度随一天中的时间而变化:
在夜间,蓝色带状区域要窄得多:这对模型非常确定会有少量的自行车租赁。而且,这些预测似乎是正确的,因为实际需求保持在蓝色带状区域内。
在白天,蓝色带状区域要宽得多:不确定性增加,可能是因为天气的变化会有很大的影响,尤其是在周末。
我们还可以看到,在工作日,通勤模式在5%和95%的估计中仍然可见。
最后,预计有10%的时间,实际需求不在5%和95%百分位估计之间。在这个测试范围内,实际需求似乎更高,尤其是在高峰时段。这可能表明我们的95%百分位估计低估了需求高峰。这可以通过计算经验覆盖率来定量确认,如在:ref:
置信区间的校准 <calibration-section>中所做的那样。
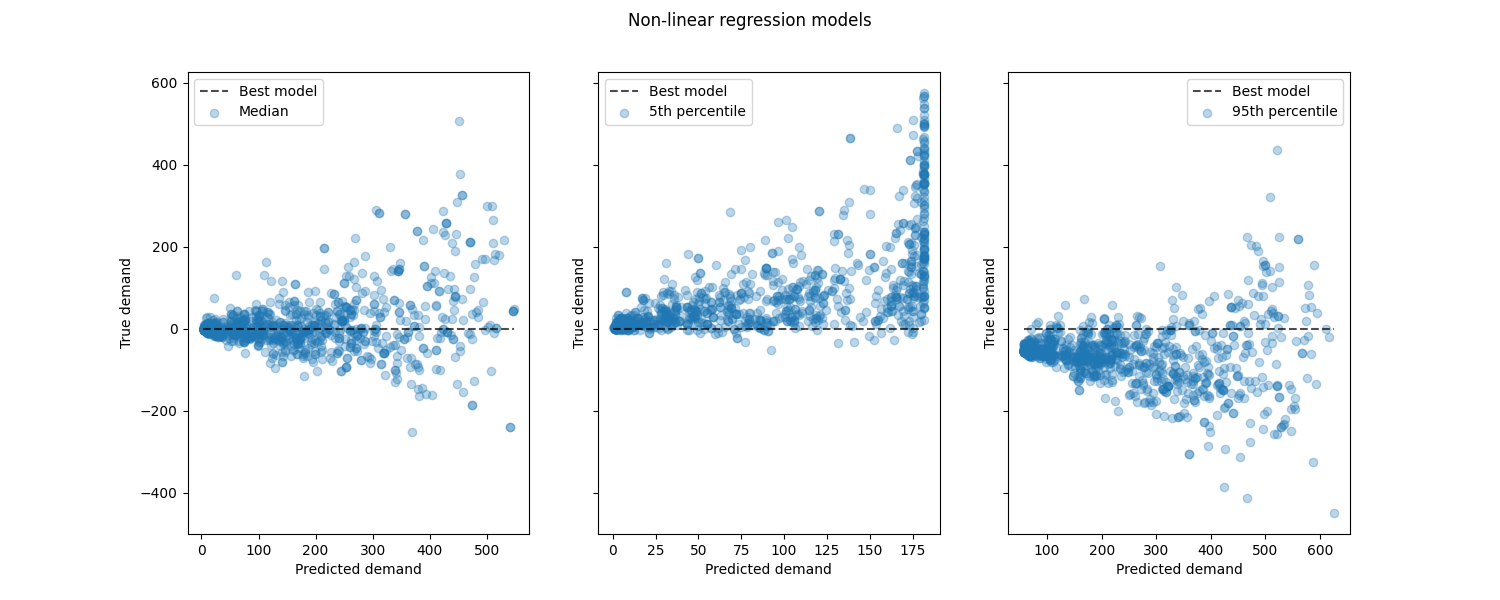
比较非线性回归模型与最佳模型的性能:
from sklearn.metrics import PredictionErrorDisplay
fig, axes = plt.subplots(ncols=3, figsize=(15, 6), sharey=True)
fig.suptitle("Non-linear regression models")
predictions = [
median_predictions,
percentile_5_predictions,
percentile_95_predictions,
]
labels = [
"Median",
"5th percentile",
"95th percentile",
]
for ax, pred, label in zip(axes, predictions, labels):
PredictionErrorDisplay.from_predictions(
y_true=y_test,
y_pred=pred,
kind="residual_vs_predicted",
scatter_kwargs={"alpha": 0.3},
ax=ax,
)
ax.set(xlabel="Predicted demand", ylabel="True demand")
ax.legend(["Best model", label])
plt.show()
结论#
通过这个例子,我们探索了使用滞后特征进行时间序列预测。我们比较了一个简单的回归(使用标准化的:class:~sklearn.model_selection.train_test_split )和一个使用:class:~sklearn.model_selection.TimeSeriesSplit 的适当时间序列评估策略。我们观察到,使用:class:~sklearn.model_selection.train_test_split 训练的模型,由于默认的 shuffle 值设置为 True ,产生了过于乐观的平均绝对百分比误差(MAPE)。基于时间分割的结果更好地代表了我们的时间序列回归模型的性能。我们还通过分位数回归分析了模型的预测不确定性。基于第5和第95百分位数的预测使用 loss="quantile" 为我们提供了时间序列回归模型预测不确定性的定量估计。不确定性估计也可以使用 MAPIE 进行,该方法基于最近的保形预测方法工作实现,同时估计了随机不确定性和认知不确定性。此外, sktime 提供的功能可以用于通过递归时间序列预测扩展scikit-learn估计器,从而实现未来值的动态预测。
Total running time of the script: (0 minutes 10.177 seconds)
Related examples