Note
Go to the end to download the full example code. or to run this example in your browser via Binder
概率校准曲线#
在进行分类时,人们通常不仅希望预测类别标签,还希望预测相关的概率。这个概率提供了对预测的一种置信度。本示例演示了如何使用校准曲线(也称为可靠性图)来可视化预测概率的校准程度。还将演示如何对未校准的分类器进行校准。
# 数据集
# -------
#
# 我们将使用一个包含100,000个样本和20个特征的合成二元分类数据集。在这20个特征中,只有2个是信息性的,10个是冗余的(信息性特征的随机组合),剩下的8个是无信息性的(随机数)。在这100,000个样本中,将使用1,000个样本进行模型拟合,其余的用于测试。
from sklearn.datasets import make_classification
from sklearn.model_selection import train_test_split
X, y = make_classification(
n_samples=100_000, n_features=20, n_informative=2, n_redundant=10, random_state=42
)
X_train, X_test, y_train, y_test = train_test_split(
X, y, test_size=0.99, random_state=42
)
校准曲线#
高斯朴素贝叶斯
首先,我们将比较:
LogisticRegression(用作基线,因为通常情况下,适当正则化的逻辑回归由于使用了对数损失,默认情况下是良好校准的)未校准的
GaussianNB经过等值和Sigmoid校准的
GaussianNB(参见 用户指南 )
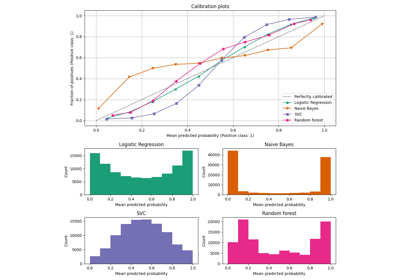
下图显示了所有4种条件的校准曲线,x轴表示每个区间的平均预测概率,y轴表示每个区间的正类比例。
import matplotlib.pyplot as plt
from matplotlib.gridspec import GridSpec
from sklearn.calibration import CalibratedClassifierCV, CalibrationDisplay
from sklearn.linear_model import LogisticRegression
from sklearn.naive_bayes import GaussianNB
lr = LogisticRegression(C=1.0)
gnb = GaussianNB()
gnb_isotonic = CalibratedClassifierCV(gnb, cv=2, method="isotonic")
gnb_sigmoid = CalibratedClassifierCV(gnb, cv=2, method="sigmoid")
clf_list = [
(lr, "Logistic"),
(gnb, "Naive Bayes"),
(gnb_isotonic, "Naive Bayes + Isotonic"),
(gnb_sigmoid, "Naive Bayes + Sigmoid"),
]
fig = plt.figure(figsize=(10, 10))
gs = GridSpec(4, 2)
colors = plt.get_cmap("Dark2")
ax_calibration_curve = fig.add_subplot(gs[:2, :2])
calibration_displays = {}
for i, (clf, name) in enumerate(clf_list):
clf.fit(X_train, y_train)
display = CalibrationDisplay.from_estimator(
clf,
X_test,
y_test,
n_bins=10,
name=name,
ax=ax_calibration_curve,
color=colors(i),
)
calibration_displays[name] = display
ax_calibration_curve.grid()
ax_calibration_curve.set_title("Calibration plots (Naive Bayes)")
# 添加直方图
grid_positions = [(2, 0), (2, 1), (3, 0), (3, 1)]
for i, (_, name) in enumerate(clf_list):
row, col = grid_positions[i]
ax = fig.add_subplot(gs[row, col])
ax.hist(
calibration_displays[name].y_prob,
range=(0, 1),
bins=10,
label=name,
color=colors(i),
)
ax.set(title=name, xlabel="Mean predicted probability", ylabel="Count")
plt.tight_layout()
plt.show()

未经校准的 GaussianNB 由于冗余特征违反了特征独立性假设,导致分类器过于自信,这通常表现为典型的转置S形曲线。因此,校准 GaussianNB 的概率可以通过 等渗回归 来解决这个问题,如几乎对角线的校准曲线所示。Sigmoid regression 也能略微改善校准效果,尽管不如非参数的等值回归强。这可以归因于我们有足够的校准数据,可以利用非参数模型的更大灵活性。
下面我们将进行定量分析,考虑几种分类指标:Brier 分数损失 、对数损失 、precision, recall, F1 score 和 ROC AUC 。
from collections import defaultdict
import pandas as pd
from sklearn.metrics import (
brier_score_loss,
f1_score,
log_loss,
precision_score,
recall_score,
roc_auc_score,
)
scores = defaultdict(list)
for i, (clf, name) in enumerate(clf_list):
clf.fit(X_train, y_train)
y_prob = clf.predict_proba(X_test)
y_pred = clf.predict(X_test)
scores["Classifier"].append(name)
for metric in [brier_score_loss, log_loss, roc_auc_score]:
score_name = metric.__name__.replace("_", " ").replace("score", "").capitalize()
scores[score_name].append(metric(y_test, y_prob[:, 1]))
for metric in [precision_score, recall_score, f1_score]:
score_name = metric.__name__.replace("_", " ").replace("score", "").capitalize()
scores[score_name].append(metric(y_test, y_pred))
score_df = pd.DataFrame(scores).set_index("Classifier")
score_df.round(decimals=3)
score_df
请注意,尽管校准提高了 Brier 分数损失 (由校准项和细化项组成的度量)和 对数损失 ,但它并不会显著改变预测准确性指标(精确度、召回率和 F1 分数)。这是因为校准不应显著改变决策阈值位置(图中 x = 0.5 处)的预测概率。然而,校准应使预测概率更准确,从而在不确定性下做出分配决策时更有用。此外,ROC AUC 不应有任何变化,因为校准是单调变换。实际上,没有任何排序指标会受到校准的影响。
线性支持向量分类器#
接下来,我们将比较:
LogisticRegression(基线)未校准的
LinearSVC。由于 SVC 默认不输出概率,我们通过应用最小-最大缩放将 decision_function 的输出简单地缩放到 [0, 1]。
import numpy as np
from sklearn.svm import LinearSVC
class NaivelyCalibratedLinearSVC(LinearSVC):
"""线性支持向量分类器(LinearSVC)带有 `predict_proba` 方法,该方法简单地缩放二分类的 `decision_function` 输出。"""
def fit(self, X, y):
super().fit(X, y)
df = self.decision_function(X)
self.df_min_ = df.min()
self.df_max_ = df.max()
def predict_proba(self, X):
"""将 `decision_function` 的输出进行 Min-max 归一化到 [0, 1]。"""
df = self.decision_function(X)
calibrated_df = (df - self.df_min_) / (self.df_max_ - self.df_min_)
proba_pos_class = np.clip(calibrated_df, 0, 1)
proba_neg_class = 1 - proba_pos_class
proba = np.c_[proba_neg_class, proba_pos_class]
return proba
lr = LogisticRegression(C=1.0)
svc = NaivelyCalibratedLinearSVC(max_iter=10_000)
svc_isotonic = CalibratedClassifierCV(svc, cv=2, method="isotonic")
svc_sigmoid = CalibratedClassifierCV(svc, cv=2, method="sigmoid")
clf_list = [
(lr, "Logistic"),
(svc, "SVC"),
(svc_isotonic, "SVC + Isotonic"),
(svc_sigmoid, "SVC + Sigmoid"),
]
fig = plt.figure(figsize=(10, 10))
gs = GridSpec(4, 2)
ax_calibration_curve = fig.add_subplot(gs[:2, :2])
calibration_displays = {}
for i, (clf, name) in enumerate(clf_list):
clf.fit(X_train, y_train)
display = CalibrationDisplay.from_estimator(
clf,
X_test,
y_test,
n_bins=10,
name=name,
ax=ax_calibration_curve,
color=colors(i),
)
calibration_displays[name] = display
ax_calibration_curve.grid()
ax_calibration_curve.set_title("Calibration plots (SVC)")
# 添加直方图
grid_positions = [(2, 0), (2, 1), (3, 0), (3, 1)]
for i, (_, name) in enumerate(clf_list):
row, col = grid_positions[i]
ax = fig.add_subplot(gs[row, col])
ax.hist(
calibration_displays[name].y_prob,
range=(0, 1),
bins=10,
label=name,
color=colors(i),
)
ax.set(title=name, xlabel="Mean predicted probability", ylabel="Count")
plt.tight_layout()
plt.show()

LinearSVC 表现出与 GaussianNB 相反的行为;校准曲线呈现出 S 形,这对于一个信心不足的分类器来说是典型的。在 LinearSVC 的情况下,这是由铰链损失的边缘属性引起的,它关注的是接近决策边界(支持向量)的样本。远离决策边界的样本不会影响铰链损失。因此,LinearSVC 不会尝试在高置信度区域分离样本是有道理的。这导致了在 0 和 1 附近较平坦的校准曲线,并在 Niculescu-Mizil & Caruana [1] 的各种数据集中得到了实证证明。
两种校准方法(S型和等温)都可以解决这个问题,并产生类似的结果。
和之前一样,我们展示了 Brier 分数损失 、对数损失 、precision, recall, F1 score 和 ROC AUC 。
scores = defaultdict(list)
for i, (clf, name) in enumerate(clf_list):
clf.fit(X_train, y_train)
y_prob = clf.predict_proba(X_test)
y_pred = clf.predict(X_test)
scores["Classifier"].append(name)
for metric in [brier_score_loss, log_loss, roc_auc_score]:
score_name = metric.__name__.replace("_", " ").replace("score", "").capitalize()
scores[score_name].append(metric(y_test, y_prob[:, 1]))
for metric in [precision_score, recall_score, f1_score]:
score_name = metric.__name__.replace("_", " ").replace("score", "").capitalize()
scores[score_name].append(metric(y_test, y_pred))
score_df = pd.DataFrame(scores).set_index("Classifier")
score_df.round(decimals=3)
score_df
与上面的 GaussianNB 类似,校准提高了 Brier 分数损失 和 对数损失 ,但对预测准确性指标(精度、召回率和 F1 分数)的影响不大。
Summary#
参数化的Sigmoid校准可以处理基分类器的校准曲线为Sigmoid的情况(例如,LinearSVC ),但不能处理其为转置Sigmoid的情况(例如,GaussianNB )。非参数的Isotonic校准可以处理这两种情况,但可能需要更多的数据来产生良好的结果。
References#
<https://dl.acm.org/doi/pdf/10.1145/1102351.1102430>`_ , A. Niculescu-Mizil 和 R. Caruana, ICML 2005
Total running time of the script: (0 minutes 1.095 seconds)
Related examples