Note
Go to the end to download the full example code. or to run this example in your browser via Binder
使用网格搜索进行模型的统计比较#
本示例说明了如何统计比较使用 GridSearchCV 训练和评估的模型的性能。
我们将从模拟月亮形状的数据开始(其中类之间的理想分离是非线性的),并添加适度的噪声。数据点将属于两个可能的类之一,这两个类将由两个特征来预测。我们将为每个类模拟50个样本:
import matplotlib.pyplot as plt
import seaborn as sns
from sklearn.datasets import make_moons
X, y = make_moons(noise=0.352, random_state=1, n_samples=100)
sns.scatterplot(
x=X[:, 0], y=X[:, 1], hue=y, marker="o", s=25, edgecolor="k", legend=False
).set_title("Data")
plt.show()

我们将比较在 kernel 参数上有所不同的 SVC 估计器的性能,以决定哪种超参数选择能最好地预测我们的模拟数据。我们将使用 RepeatedStratifiedKFold 来评估模型的性能,重复 10 次 10 折分层交叉验证,每次重复使用不同的随机数据。性能将使用 roc_auc_score 进行评估。
from sklearn.model_selection import GridSearchCV, RepeatedStratifiedKFold
from sklearn.svm import SVC
param_grid = [
{"kernel": ["linear"]},
{"kernel": ["poly"], "degree": [2, 3]},
{"kernel": ["rbf"]},
]
svc = SVC(random_state=0)
cv = RepeatedStratifiedKFold(n_splits=10, n_repeats=10, random_state=0)
search = GridSearchCV(estimator=svc, param_grid=param_grid, scoring="roc_auc", cv=cv)
search.fit(X, y)
我们现在可以查看搜索结果,按其 mean_test_score 排序:
import pandas as pd
results_df = pd.DataFrame(search.cv_results_)
results_df = results_df.sort_values(by=["rank_test_score"])
results_df = results_df.set_index(
results_df["params"].apply(lambda x: "_".join(str(val) for val in x.values()))
).rename_axis("kernel")
results_df[["params", "rank_test_score", "mean_test_score", "std_test_score"]]
我们可以看到,使用 'rbf' 核的估计器表现最好,其次是 'linear' 。使用 'poly' 核的两个估计器表现较差,其中使用二次多项式的估计器表现远低于所有其他模型。
通常,分析到此就结束了,但这只是故事的一半。GridSearchCV 的输出并未提供模型之间差异的确定性信息。我们不知道这些差异是否具有**统计**显著性。为了评估这一点,我们需要进行统计检验。具体来说,为了对比两个模型的性能,我们应该统计比较它们的AUC分数。由于我们进行了10次10折交叉验证,每个模型有100个样本(AUC分数)。
然而,这些模型的评分并不是独立的:所有模型都在相同的100个分区上进行评估,这增加了模型性能之间的相关性。由于某些数据分区可能会使所有模型的类别区分变得特别容易或困难,模型评分将会共同变化。
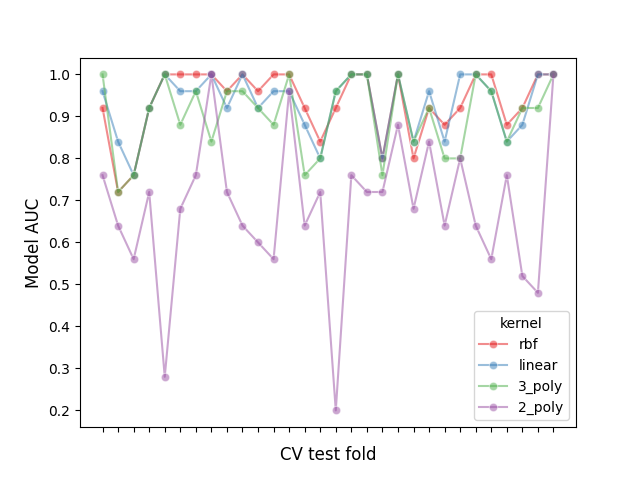
让我们通过绘制每个折叠中所有模型的性能图,并计算跨折叠的模型之间的相关性来检查这种分区效应:
# 创建按性能排序的模型评分数据框
model_scores = results_df.filter(regex=r"split\d*_test_score")
# 绘制30个关于交叉验证折叠和AUC分数之间依赖关系的示例
fig, ax = plt.subplots()
sns.lineplot(
data=model_scores.transpose().iloc[:30],
dashes=False,
palette="Set1",
marker="o",
alpha=0.5,
ax=ax,
)
ax.set_xlabel("CV test fold", size=12, labelpad=10)
ax.set_ylabel("Model AUC", size=12)
ax.tick_params(bottom=True, labelbottom=False)
plt.show()
# 打印各折叠间AUC分数的相关性
print(f"Correlation of models:\n {model_scores.transpose().corr()}")
Correlation of models:
kernel rbf linear 3_poly 2_poly
kernel
rbf 1.000000 0.882561 0.783392 0.351390
linear 0.882561 1.000000 0.746492 0.298688
3_poly 0.783392 0.746492 1.000000 0.355440
2_poly 0.351390 0.298688 0.355440 1.000000
我们可以观察到模型的性能高度依赖于折叠。
因此,如果我们假设样本之间是独立的,我们将在统计测试中低估计算出的方差,从而增加假阳性错误的数量(即在模型之间不存在显著差异时检测到显著差异)[1]_。
已经为这些情况开发了几种方差校正的统计检验。在这个例子中,我们将展示如何在两种不同的统计框架下(即所谓的Nadeau和Bengio校正t检验)实现其中之一:频率主义和贝叶斯主义。
比较两个模型:频率论方法#
我们可以先问:“第一个模型是否显著优于第二个模型(按 mean_test_score 排名)?”
为了使用频率学方法回答这个问题,我们可以运行配对t检验并计算p值。这在预测文献中也被称为Diebold-Mariano检验 [5]。为了应对前一节中描述的“样本非独立性问题”,已经开发了许多这种t检验的变体。我们将使用一种被证明在保持低假阳性和假阴性率的同时,获得最高可重复性评分(即在对同一数据集的不同随机分区进行评估时,模型性能的相似程度)的检验方法:Nadeau和Bengio修正的t检验 [2],该方法使用10次重复的10折交叉验证 [3]。
这个修正后的配对t检验计算如下:
t=frac{frac{1}{k cdot r}sum_{i=1}^{k}sum_{j=1}^{r}x_{ij}} {sqrt{(frac{1}{k cdot r}+frac{n_{test}}{n_{train}})hat{sigma}^2}}
其中 \(k\) 是折数,\(r\) 是交叉验证中的重复次数,\(x\) 是模型性能的差异,\(n_{test}\) 是用于测试的样本数量,\(n_{train}\) 是用于训练的样本数量,\(\hat{\sigma}^2\) 表示观察到的差异的方差。
让我们实现一个修正的右尾配对t检验,以评估第一个模型的性能是否显著优于第二个模型。我们的原假设是第二个模型的性能至少与第一个模型一样好。
import numpy as np
from scipy.stats import t
def corrected_std(differences, n_train, n_test):
"""修正标准差使用Nadeau和Bengio的方法。
Parameters
----------
differences : ndarray,形状为 (n_samples,)
包含两个模型评分指标差异的向量。
n_train : int
训练集中的样本数量。
n_test : int
测试集中的样本数量。
返回
-------
corrected_std : float
差异集的方差修正标准差。
"""
# kr 是 k 乘以 r,r 次重复的 k 折交叉验证,
# kr 等于模型被评估的次数
kr = len(differences)
corrected_var = np.var(differences, ddof=1) * (1 / kr + n_test / n_train)
corrected_std = np.sqrt(corrected_var)
return corrected_std
def compute_corrected_ttest(differences, df, n_train, n_test):
"""计算右尾配对t检验,并校正方差。
Parameters
----------
differences : 形状为 (n_samples,) 的类数组
包含两个模型评分指标差异的向量。
df : int
自由度。
n_train : int
训练集中的样本数量。
n_test : int
测试集中的样本数量。
Returns
-------
t_stat : float
校正方差后的t统计量。
p_val : float
校正方差后的p值。
"""
mean = np.mean(differences)
std = corrected_std(differences, n_train, n_test)
t_stat = mean / std
p_val = t.sf(np.abs(t_stat), df) # right-tailed t-test
return t_stat, p_val
model_1_scores = model_scores.iloc[0].values # scores of the best model
model_2_scores = model_scores.iloc[1].values # scores of the second-best model
differences = model_1_scores - model_2_scores
n = differences.shape[0] # number of test sets
df = n - 1
n_train = len(list(cv.split(X, y))[0][0])
n_test = len(list(cv.split(X, y))[0][1])
t_stat, p_val = compute_corrected_ttest(differences, df, n_train, n_test)
print(f"Corrected t-value: {t_stat:.3f}\nCorrected p-value: {p_val:.3f}")
Corrected t-value: 0.750
Corrected p-value: 0.227
我们可以将校正后的t值和p值与未校正的进行比较:
Uncorrected t-value: 2.611
Uncorrected p-value: 0.005
使用常规显著性水平α=0.05,我们观察到未经校正的t检验得出结论,第一个模型显著优于第二个模型。
相比之下,使用修正后的方法,我们未能检测到这一差异。
然而,在后一种情况下,频率学派的方法并不允许我们得出第一个模型和第二个模型具有相同性能的结论。如果我们想做出这种断言,我们需要使用贝叶斯方法。
比较两个模型:贝叶斯方法#
我们可以使用贝叶斯估计来计算第一个模型优于第二个模型的概率。贝叶斯估计将输出一个分布,随后是两个模型性能差异的均值 \(\mu\) 。
为了获得后验分布,我们需要定义一个先验分布,该分布在查看数据之前建模我们对均值分布的信念,并将其乘以似然函数,该函数计算在给定均值可能取值的情况下,我们观察到的差异的可能性。
贝叶斯估计可以通过多种形式来回答我们的问题,但在这个例子中,我们将实现Benavoli及其同事[4]_建议的方法。
一种使用闭式表达式定义后验的方法是选择一个与似然函数共轭的先验。Benavoli及其同事[4]表明,在比较两个分类器的性能时,我们可以将先验建模为正态-伽马分布(均值和方差均未知),与正态似然函数共轭,从而将后验表达为正态分布。从这个正态后验中边缘化方差后,我们可以将均值参数的后验定义为学生t分布。具体来说:
St(mu;n-1,overline{x},(frac{1}{n}+frac{n_{test}}{n_{train}}) hat{sigma}^2)
其中 \(n\) 是样本总数, \(\overline{x}\) 表示分数的平均差, \(n_{test}\) 是用于测试的样本数, \(n_{train}\) 是用于训练的样本数, \(\hat{\sigma}^2\) 表示观测差异的方差。
请注意,我们在贝叶斯方法中也使用了Nadeau和Bengio校正的方差。
让我们计算并绘制后验分布:
让我们绘制后验分布:
x = np.linspace(t_post.ppf(0.001), t_post.ppf(0.999), 100)
plt.plot(x, t_post.pdf(x))
plt.xticks(np.arange(-0.04, 0.06, 0.01))
plt.fill_between(x, t_post.pdf(x), 0, facecolor="blue", alpha=0.2)
plt.ylabel("Probability density")
plt.xlabel(r"Mean difference ($\mu$)")
plt.title("Posterior distribution")
plt.show()

我们可以通过计算后验分布曲线从零到无穷大的面积来计算第一个模型优于第二个模型的概率。同样,我们也可以通过计算曲线从负无穷大到零的面积来计算第二个模型优于第一个模型的概率。
better_prob = 1 - t_post.cdf(0)
print(
f"Probability of {model_scores.index[0]} being more accurate than "
f"{model_scores.index[1]}: {better_prob:.3f}"
)
print(
f"Probability of {model_scores.index[1]} being more accurate than "
f"{model_scores.index[0]}: {1 - better_prob:.3f}"
)
Probability of rbf being more accurate than linear: 0.773
Probability of linear being more accurate than rbf: 0.227
与频率派方法相反,我们可以计算一个模型优于另一个模型的概率。
请注意,我们获得的结果与频率学派方法中的结果相似。鉴于我们选择的先验分布,我们实际上在执行相同的计算,但我们可以做出不同的断言。
实际等效区域#
有时我们感兴趣的是确定我们的模型具有等效性能的概率,其中“等效”是以实际方式定义的。一种简单的方法 [4] 是在估计器的准确率相差不到1%时将其定义为实际等效。但我们也可以根据我们试图解决的问题来定义这种实际等效性。例如,准确率相差5%意味着销售额增加$1000,我们认为任何超过这个数量的差异对我们的业务都是重要的。
在这个例子中,我们将实际等效区间(ROPE)定义为 \([-0.01, 0.01]\) 。也就是说,如果两个模型在性能上相差不到1%,我们将认为它们在实际应用中是等效的。
为了计算分类器在实际等效情况下的概率,我们计算ROPE区间后验分布曲线下的面积:
rope_interval = [-0.01, 0.01]
rope_prob = t_post.cdf(rope_interval[1]) - t_post.cdf(rope_interval[0])
print(
f"Probability of {model_scores.index[0]} and {model_scores.index[1]} "
f"being practically equivalent: {rope_prob:.3f}"
)
Probability of rbf and linear being practically equivalent: 0.432
我们可以绘制后验分布在ROPE区间上的分布情况:
x_rope = np.linspace(rope_interval[0], rope_interval[1], 100)
plt.plot(x, t_post.pdf(x))
plt.xticks(np.arange(-0.04, 0.06, 0.01))
plt.vlines([-0.01, 0.01], ymin=0, ymax=(np.max(t_post.pdf(x)) + 1))
plt.fill_between(x_rope, t_post.pdf(x_rope), 0, facecolor="blue", alpha=0.2)
plt.ylabel("Probability density")
plt.xlabel(r"Mean difference ($\mu$)")
plt.title("Posterior distribution under the ROPE")
plt.show()
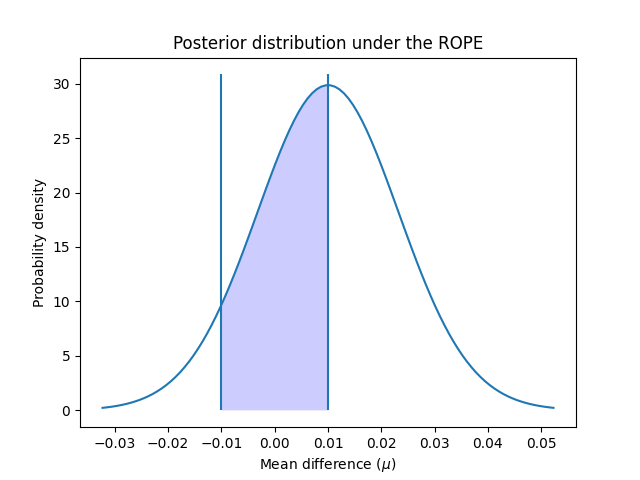
根据文献[4]的建议,我们可以使用与频率学派方法相同的标准进一步解释这些概率:落在ROPE内的概率是否大于95%(alpha值为5%)?在这种情况下,我们可以得出结论,两个模型在实际意义上是等效的。
贝叶斯估计方法还允许我们计算对差异估计的不确定性。这可以使用可信区间来计算。对于给定的概率,它们显示了估计量(在我们的例子中是性能均值差异)可以取的值范围。 例如,50%的可信区间 [x, y] 告诉我们,模型之间性能的真实(均值)差异在 x 和 y 之间的概率为 50%。
让我们使用50%、75%和95%来确定我们数据的可信区间:
cred_intervals = []
intervals = [0.5, 0.75, 0.95]
for interval in intervals:
cred_interval = list(t_post.interval(interval))
cred_intervals.append([interval, cred_interval[0], cred_interval[1]])
cred_int_df = pd.DataFrame(
cred_intervals, columns=["interval", "lower value", "upper value"]
).set_index("interval")
cred_int_df
如表所示,模型之间真实均值差异在0.000977到0.019023之间的概率为50%,在-0.005422到0.025422之间的概率为70%,在-0.016445到0.036445之间的概率为95%。
成对比较所有模型:频率论方法#
我们也可能对比较所有使用 GridSearchCV 评估的模型的性能感兴趣。在这种情况下,我们将多次运行统计测试,这会导致 多重比较问题 。
有很多方法可以解决这个问题,但一种标准方法是应用 Bonferroni校正 。Bonferroni校正可以通过将p值乘以我们正在测试的比较次数来计算。
让我们使用修正后的t检验来比较模型的性能:
from itertools import combinations
from math import factorial
n_comparisons = factorial(len(model_scores)) / (
factorial(2) * factorial(len(model_scores) - 2)
)
pairwise_t_test = []
for model_i, model_k in combinations(range(len(model_scores)), 2):
model_i_scores = model_scores.iloc[model_i].values
model_k_scores = model_scores.iloc[model_k].values
differences = model_i_scores - model_k_scores
t_stat, p_val = compute_corrected_ttest(differences, df, n_train, n_test)
p_val *= n_comparisons # implement Bonferroni correction
# Bonferroni 可能输出大于 1 的 p 值
p_val = 1 if p_val > 1 else p_val
pairwise_t_test.append(
[model_scores.index[model_i], model_scores.index[model_k], t_stat, p_val]
)
pairwise_comp_df = pd.DataFrame(
pairwise_t_test, columns=["model_1", "model_2", "t_stat", "p_val"]
).round(3)
pairwise_comp_df
我们观察到,在校正多重比较后,唯一显著不同于其他模型的是 '2_poly' 。由 GridSearchCV 排名第一的模型 'rbf' ,与 'linear' 或 '3_poly' 并无显著差异。
成对比较所有模型:贝叶斯方法#
在使用贝叶斯估计比较多个模型时,我们不需要进行多重比较校正(原因见[4]_)。
我们可以像在第一部分中一样进行成对比较:
pairwise_bayesian = []
for model_i, model_k in combinations(range(len(model_scores)), 2):
model_i_scores = model_scores.iloc[model_i].values
model_k_scores = model_scores.iloc[model_k].values
differences = model_i_scores - model_k_scores
t_post = t(
df, loc=np.mean(differences), scale=corrected_std(differences, n_train, n_test)
)
worse_prob = t_post.cdf(rope_interval[0])
better_prob = 1 - t_post.cdf(rope_interval[1])
rope_prob = t_post.cdf(rope_interval[1]) - t_post.cdf(rope_interval[0])
pairwise_bayesian.append([worse_prob, better_prob, rope_prob])
pairwise_bayesian_df = pd.DataFrame(
pairwise_bayesian, columns=["worse_prob", "better_prob", "rope_prob"]
).round(3)
pairwise_comp_df = pairwise_comp_df.join(pairwise_bayesian_df)
pairwise_comp_df
使用贝叶斯方法,我们可以计算出一个模型比另一个模型表现更好、更差或几乎相同的概率。
结果显示,模型在 GridSearchCV 中排名第一的 'rbf' ,有大约 6.8% 的可能性比 'linear' 差,有 1.8% 的可能性比 '3_poly' 差。 'rbf' 和 'linear' 有 43% 的概率在实际效果上相当,而 'rbf' 和 '3_poly' 有 10% 的概率相当。
同样地,与使用频率论方法得出的结论类似,所有模型都有100%的概率优于 '2_poly' ,且没有任何模型与其表现几乎相同。
家庭作业要点#
性能指标的微小差异很可能只是偶然现象,而不是因为一个模型系统性地比另一个模型预测得更好。如本例所示,统计数据可以告诉你这种情况的可能性有多大。
在统计比较通过GridSearchCV评估的两个模型的性能时,有必要修正计算的方差,因为模型的得分不是相互独立的,可能会被低估。
使用(方差修正的)配对t检验的频率学方法可以告诉我们一个模型的性能是否比另一个模型好,并且这种确定性高于偶然性。
贝叶斯方法可以提供一个模型比另一个模型更好、更差或几乎相等的概率。它还可以告诉我们,知道模型的真实差异落在某个值范围内的置信度有多高。
如果对多个模型进行统计比较,在使用频率学方法时需要进行多重比较校正。
参考文献
Total running time of the script: (0 minutes 0.658 seconds)
Related examples