Note
Go to the end to download the full example code. or to run this example in your browser via Binder
使用不同SVM核函数绘制分类边界#
此示例展示了在二元二维分类问题中,不同的 SVC (支持向量分类器)核函数如何影响分类边界。
SVC旨在通过最大化每个类别最外层数据点之间的间隔,找到有效分离训练数据中类别的超平面。这是通过找到最佳权重向量 \(w\) 来实现的,该向量定义了决策边界超平面,并最小化由 hinge_loss 函数测量的误分类样本的铰链损失之和。默认情况下,使用参数 C=1 进行正则化,这允许一定程度的误分类容忍度。
如果数据在原始特征空间中不是线性可分的,可以设置非线性核参数。根据核函数的不同,过程涉及添加新特征或转换现有特征以丰富并可能为数据添加意义。当设置了 "linear" 以外的核函数时,SVC应用 核技巧 _,该技巧使用核函数计算数据点对之间的相似性,而无需显式转换整个数据集。核技巧通过仅考虑所有数据点对之间的关系,超越了对整个数据集进行矩阵转换的必要性。核函数使用点积将两个向量(每对观测值)映射到它们的相似性。
然后可以使用核函数计算超平面,就像数据集表示在更高维空间中一样。使用核函数而不是显式矩阵转换提高了性能,因为核函数的时间复杂度为 \(O({n}^2)\) ,而矩阵转换的复杂度取决于所应用的具体转换。
在此示例中,我们比较了支持向量机最常见的核类型:线性核( "linear" )、多项式核( "poly" )、径向基函数核( "rbf" )和S型核( "sigmoid" )。
# 代码来源:Gaël Varoquaux
# SPDX-License-Identifier:BSD-3-Clause
创建数据集#
我们创建了一个包含16个样本和两个类别的二维分类数据集。我们用与其各自目标相匹配的颜色绘制样本。
import matplotlib.pyplot as plt
import numpy as np
X = np.array(
[
[0.4, -0.7],
[-1.5, -1.0],
[-1.4, -0.9],
[-1.3, -1.2],
[-1.1, -0.2],
[-1.2, -0.4],
[-0.5, 1.2],
[-1.5, 2.1],
[1.0, 1.0],
[1.3, 0.8],
[1.2, 0.5],
[0.2, -2.0],
[0.5, -2.4],
[0.2, -2.3],
[0.0, -2.7],
[1.3, 2.1],
]
)
y = np.array([0, 0, 0, 0, 0, 0, 0, 0, 1, 1, 1, 1, 1, 1, 1, 1])
# 绘图设置
fig, ax = plt.subplots(figsize=(4, 3))
x_min, x_max, y_min, y_max = -3, 3, -3, 3
ax.set(xlim=(x_min, x_max), ylim=(y_min, y_max))
# 按颜色绘制样本并添加图例
scatter = ax.scatter(X[:, 0], X[:, 1], s=150, c=y, label=y, edgecolors="k")
ax.legend(*scatter.legend_elements(), loc="upper right", title="Classes")
ax.set_title("Samples in two-dimensional feature space")
_ = plt.show()
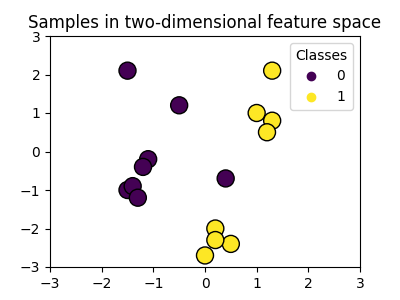
我们可以看到,这些样本无法通过一条直线清晰地分开。
训练SVC模型并绘制决策边界#
我们定义了一个函数,该函数拟合一个:class:~sklearn.svm.SVC 分类器,允许将 kernel 参数作为输入,然后使用:class:~sklearn.inspection.DecisionBoundaryDisplay 绘制模型学习到的决策边界。
请注意,为了简化起见,在此示例中, C 参数设置为其默认值 ( C=1 ),并且 gamma 参数在所有核函数中都设置为 gamma=2 ,尽管对于线性核函数它会被自动忽略。在实际的分类任务中,如果性能很重要,强烈建议进行参数调优(例如使用 GridSearchCV )以捕捉数据中的不同结构。
将 response_method="predict" 设置在 DecisionBoundaryDisplay 中时,会根据预测类别对区域进行着色。使用 response_method="decision_function" 还可以绘制决策边界及其两侧的边缘。最后,通过训练好的 SVC 的 support_vectors_ 属性来识别训练期间使用的支持向量(它们总是位于边缘上),并将其绘制出来。
from sklearn import svm
from sklearn.inspection import DecisionBoundaryDisplay
def plot_training_data_with_decision_boundary(
kernel, ax=None, long_title=True, support_vectors=True
):
# 训练支持向量机分类器
clf = svm.SVC(kernel=kernel, gamma=2).fit(X, y)
# 绘图设置
if ax is None:
_, ax = plt.subplots(figsize=(4, 3))
x_min, x_max, y_min, y_max = -3, 3, -3, 3
ax.set(xlim=(x_min, x_max), ylim=(y_min, y_max))
# 绘制决策边界和边距
common_params = {"estimator": clf, "X": X, "ax": ax}
DecisionBoundaryDisplay.from_estimator(
**common_params,
response_method="predict",
plot_method="pcolormesh",
alpha=0.3,
)
DecisionBoundaryDisplay.from_estimator(
**common_params,
response_method="decision_function",
plot_method="contour",
levels=[-1, 0, 1],
colors=["k", "k", "k"],
linestyles=["--", "-", "--"],
)
if support_vectors:
# 在作为支持向量的样本周围绘制更大的圆圈
ax.scatter(
clf.support_vectors_[:, 0],
clf.support_vectors_[:, 1],
s=150,
facecolors="none",
edgecolors="k",
)
# 按颜色绘制样本并添加图例
ax.scatter(X[:, 0], X[:, 1], c=y, s=30, edgecolors="k")
ax.legend(*scatter.legend_elements(), loc="upper right", title="Classes")
if long_title:
ax.set_title(f" Decision boundaries of {kernel} kernel in SVC")
else:
ax.set_title(kernel)
if ax is None:
plt.show()
线性核#
线性核是输入样本的点积:
然后将其应用于数据集中任意两个数据点(样本)的组合。两点的点积决定了两点之间的
cosine_similarity 。值越高,点越相似。
plot_training_data_with_decision_boundary("linear")
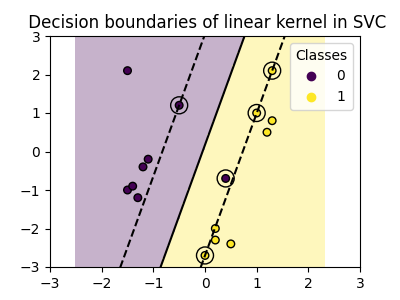
使用线性核训练 SVC 会导致未变换的特征空间,其中超平面和边界是直线。由于线性核的表达能力不足,训练的类别不能完美地捕捉训练数据。
多项式核#
多项式核改变了相似性的概念。核函数定义为:
K(mathbf{x}_1, mathbf{x}_2) = (gamma cdot mathbf{x}_1^topmathbf{x}_2 + r)^d
其中 \({d}\) 是多项式的次数( degree ),\({\gamma}\) ( gamma )控制每个训练样本对决策边界的影响,\({r}\) 是偏置项( coef0 ),用于将数据上移或下移。这里,我们使用核函数中多项式次数的默认值( degree=3 )。当 coef0=0 (默认值)时,数据仅被转换,但不会增加额外的维度。使用多项式核等价于创建 PolynomialFeatures ,然后在转换后的数据上拟合一个线性核的 SVC ,尽管这种替代方法对于大多数数据集来说在计算上是昂贵的。
plot_training_data_with_decision_boundary("poly")
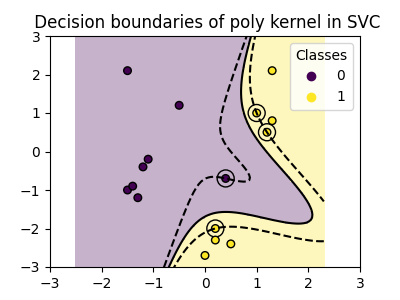
多项式核函数 gamma=2 能很好地适应训练数据,使得超平面两侧的边界相应地弯曲。
径向基函数(RBF)核#
径向基函数(RBF)核,也称为高斯核,是scikit-learn中支持向量机的默认核。它在无限维度中测量两个数据点之间的相似性,然后通过多数投票进行分类。核函数定义为:
K(mathbf{x}_1, mathbf{x}_2) = expleft(-gamma cdot {|mathbf{x}_1 - mathbf{x}_2|^2}right)
其中 \({\gamma}\) ( gamma ) 控制每个训练样本对决策边界的影响。
两点之间的欧几里得距离越大 \(\|\mathbf{x}_1 - \mathbf{x}_2\|^2\) 核函数就越接近于零。这意味着距离较远的两点更有可能是不相似的。
plot_training_data_with_decision_boundary("rbf")
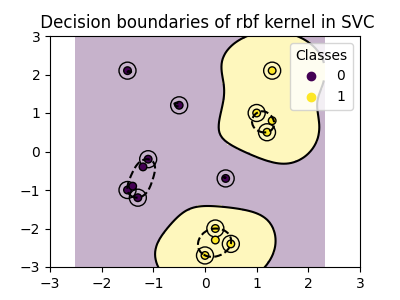
在图中我们可以看到决策边界如何趋向于收缩在彼此接近的数据点周围。
Sigmoid 核函数#
Sigmoid 核函数定义为:
K(mathbf{x}_1, mathbf{x}_2) = tanh(gamma cdot mathbf{x}_1^topmathbf{x}_2 + r)
其中核系数 \({\gamma}\) ( gamma )控制每个单独训练样本对决策边界的影响,而 \({r}\) 是偏置项( coef0 ),用于将数据上移或下移。
在S型核中,两个数据点之间的相似性是使用双曲正切函数(\(\tanh\) )计算的。核函数对两个点(\(\mathbf{x}_1\) 和:math:mathbf{x}_2 )的点积进行缩放并可能进行平移。
plot_training_data_with_decision_boundary("sigmoid")
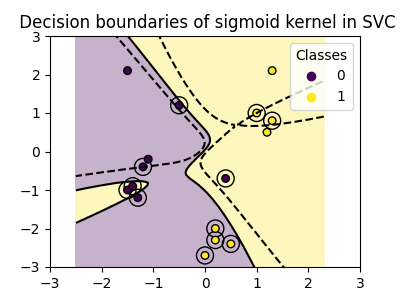
我们可以看到,使用S型核函数得到的决策边界呈现出弯曲和不规则的形状。决策边界试图通过拟合一个S型曲线来分隔类别,导致了一个复杂的边界,这可能无法很好地推广到未见过的数据。从这个例子中可以明显看出,S型核函数在处理呈现S型形状的数据时有非常具体的用例。在这个例子中,仔细的微调可能会找到更具普遍性的决策边界。由于其特异性,S型核函数在实践中不如其他核函数常用。
结论#
在这个示例中,我们可视化了使用提供的数据集训练的决策边界。这些图表直观地展示了不同的核函数如何利用训练数据来确定分类边界。
超平面和边界虽然是间接计算的,但可以想象为变换后的特征空间中的平面。然而,在图中,它们是相对于原始特征空间表示的,这导致多项式、RBF和Sigmoid核的决策边界呈现曲线。
请注意,这些图表并不评估各个核的准确性或质量。它们旨在提供对不同核如何使用训练数据的直观理解。
为了进行全面评估,建议使用诸如 GridSearchCV 等技术对 SVC 参数进行微调,以捕捉数据中的潜在结构。
XOR 数据集#
一个经典的非线性可分数据集示例是 XOR 模式。这里我们展示了不同的核函数在这种数据集上的表现。
xx, yy = np.meshgrid(np.linspace(-3, 3, 500), np.linspace(-3, 3, 500))
np.random.seed(0)
X = np.random.randn(300, 2)
y = np.logical_xor(X[:, 0] > 0, X[:, 1] > 0)
_, ax = plt.subplots(2, 2, figsize=(8, 8))
args = dict(long_title=False, support_vectors=False)
plot_training_data_with_decision_boundary("linear", ax[0, 0], **args)
plot_training_data_with_decision_boundary("poly", ax[0, 1], **args)
plot_training_data_with_decision_boundary("rbf", ax[1, 0], **args)
plot_training_data_with_decision_boundary("sigmoid", ax[1, 1], **args)
plt.show()
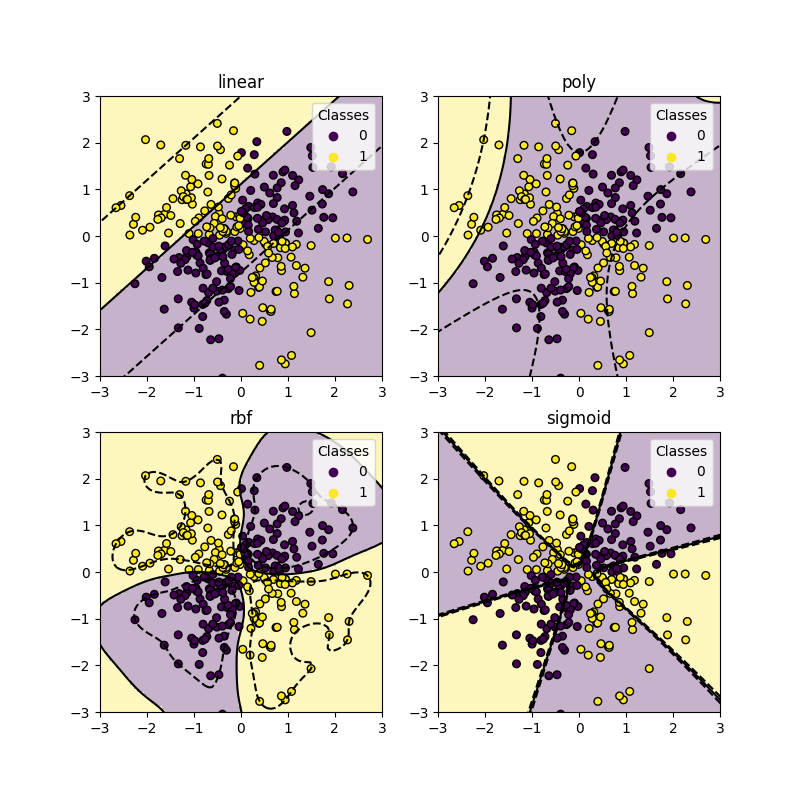
正如你从上面的图表中所看到的,只有 rbf 核能够为上述数据集找到一个合理的决策边界。
Total running time of the script: (0 minutes 0.622 seconds)
Related examples