Note

Go to the end to download the full example code. or to run this example in your browser via Binder

使用轮廓分析选择KMeans聚类的簇数#

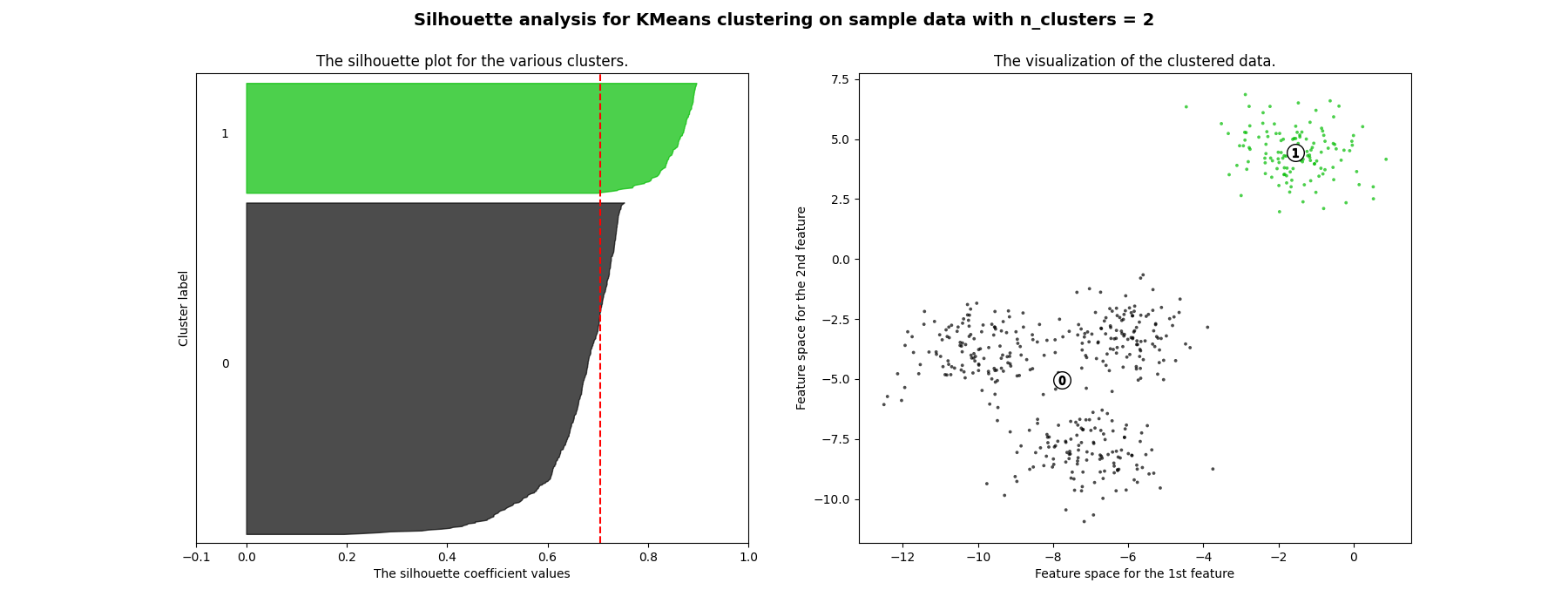
轮廓分析可用于研究生成的簇之间的分离距离。轮廓图显示了一个度量，表示一个簇中的每个点与相邻簇中的点有多接近，从而提供了一种直观评估簇数等参数的方法。该度量的范围是[-1, 1]。

轮廓系数（即这些值）接近+1表示样本远离相邻簇。值为0表示样本位于两个相邻簇之间的决策边界上或非常接近决策边界，负值表示这些样本可能被分配到了错误的簇。

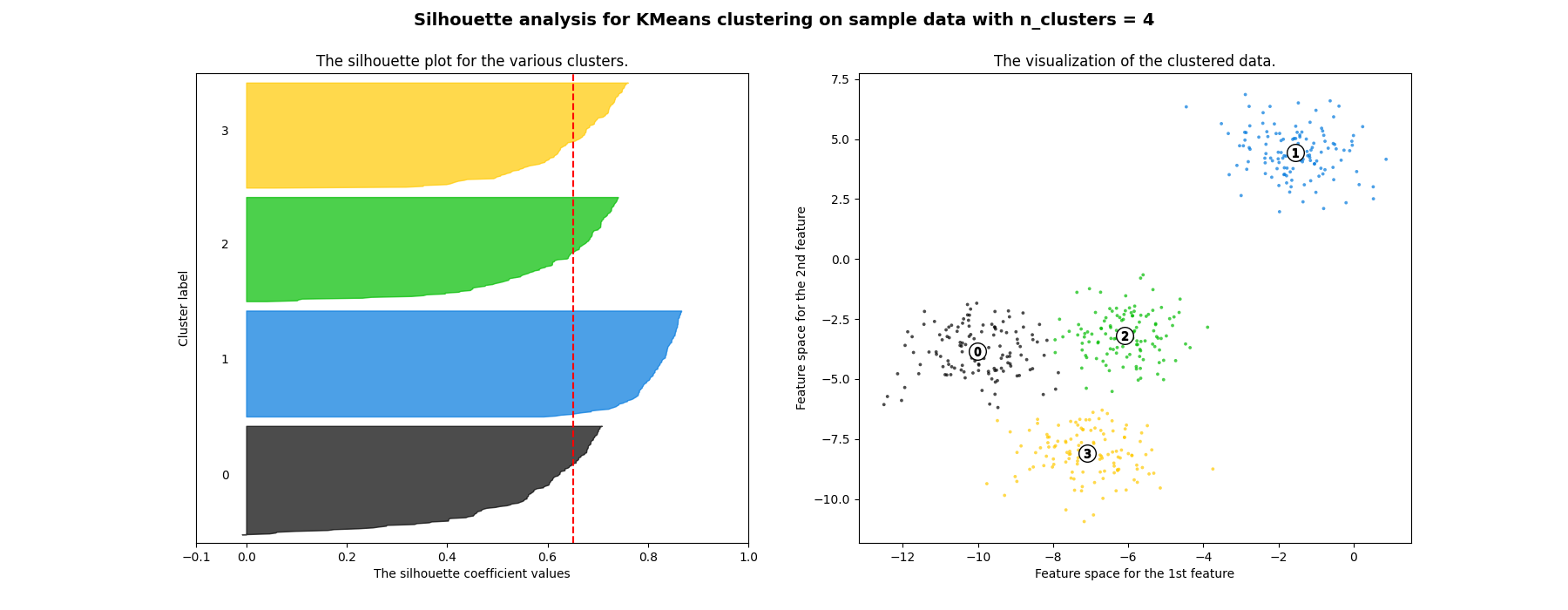
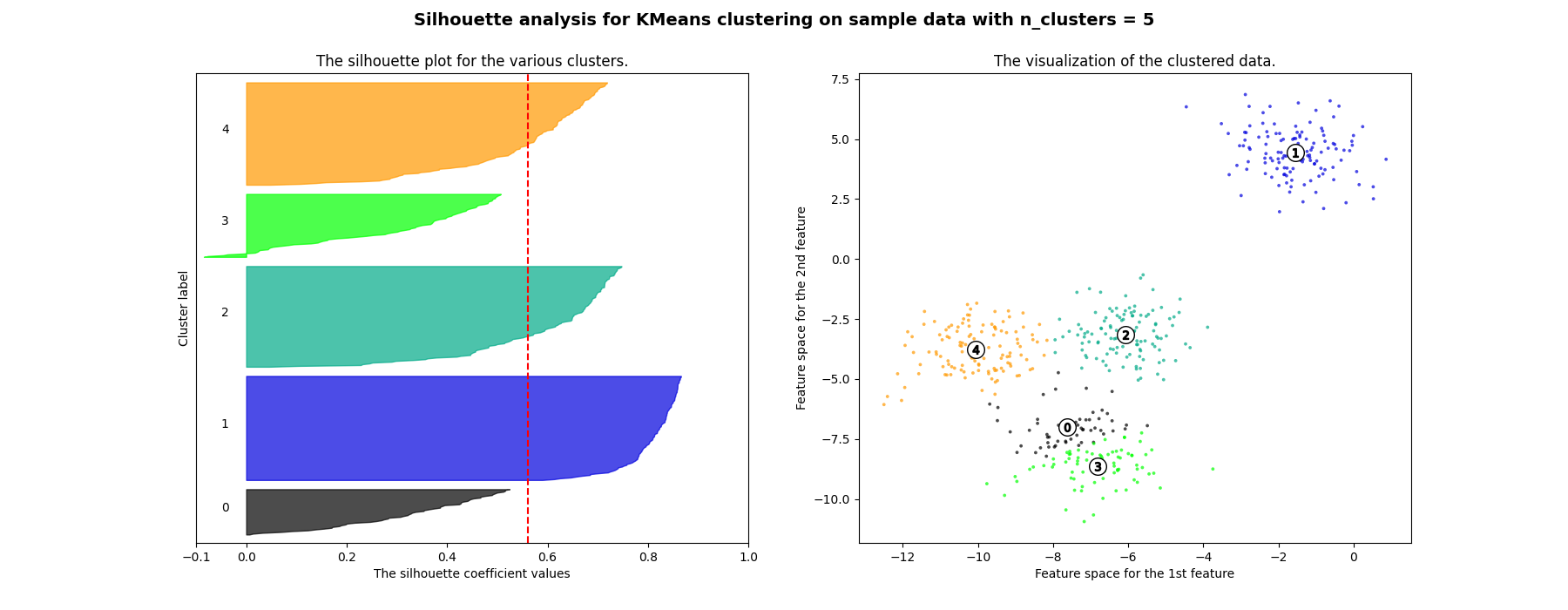
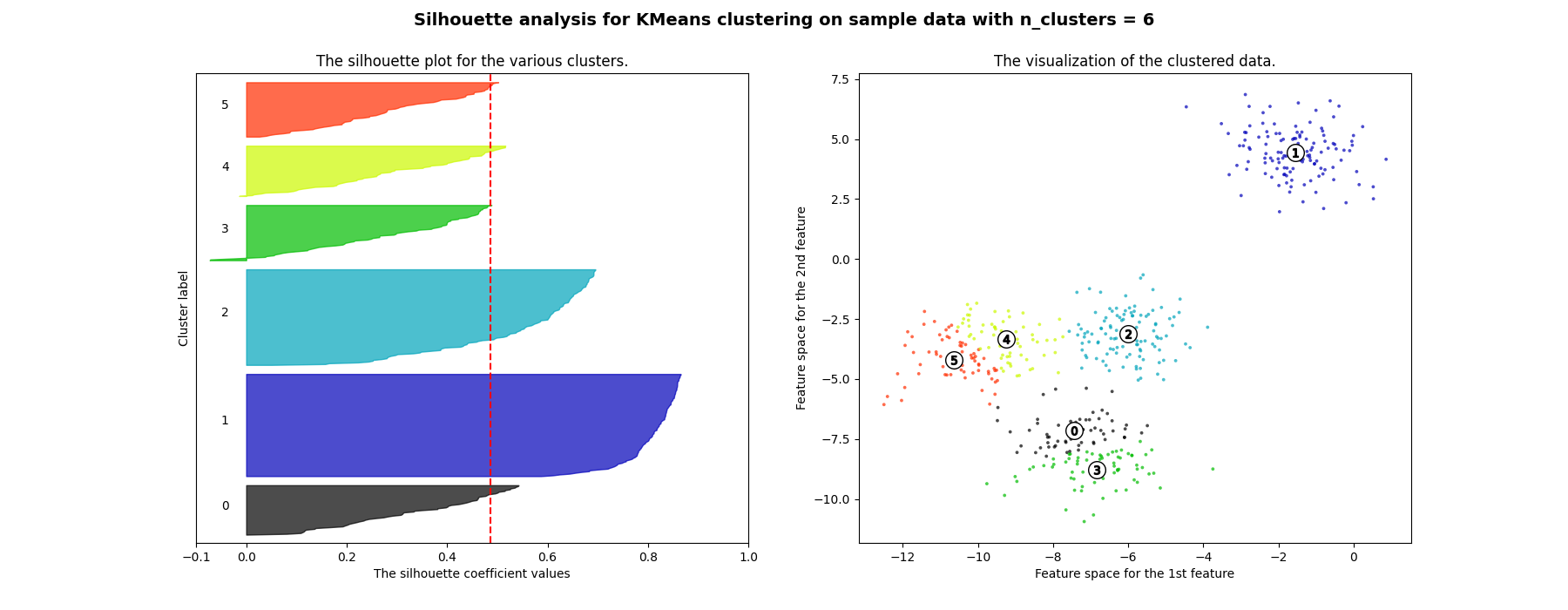
在此示例中，轮廓分析用于选择 n_clusters 的最佳值。轮廓图显示，由于存在低于平均轮廓得分的簇以及轮廓图大小的巨大波动， n_clusters 值为3、5和6对于给定数据来说是一个糟糕的选择。轮廓分析在2和4之间的选择上更为模棱两可。

此外，从轮廓图的厚度可以直观地看到簇的大小。当 n_clusters 等于2时，簇0的轮廓图由于将3个子簇分组为一个大簇而更大。然而，当 n_clusters 等于4时，所有图的厚度大致相同，因此大小也相似，这也可以从右侧标记的散点图中验证。

For n_clusters = 2 The average silhouette_score is : 0.7049787496083262
For n_clusters = 3 The average silhouette_score is : 0.5882004012129721
For n_clusters = 4 The average silhouette_score is : 0.6505186632729437
For n_clusters = 5 The average silhouette_score is : 0.561464362648773
For n_clusters = 6 The average silhouette_score is : 0.4857596147013469

import matplotlib.cm as cm
import matplotlib.pyplot as plt
import numpy as np

from sklearn.cluster import KMeans
from sklearn.datasets import make_blobs
from sklearn.metrics import silhouette_samples, silhouette_score

# 生成样本数据来自 make_blobs
# 这种特定设置有一个独特的簇和三个靠得很近的簇。
X, y = make_blobs(
    n_samples=500,
    n_features=2,
    centers=4,
    cluster_std=1,
    center_box=(-10.0, 10.0),
    shuffle=True,
    random_state=1,
)  # For reproducibility

range_n_clusters = [2, 3, 4, 5, 6]

for n_clusters in range_n_clusters:
    # 创建一个包含1行2列的子图
    fig, (ax1, ax2) = plt.subplots(1, 2)
    fig.set_size_inches(18, 7)

    # 第一个子图是轮廓图
    # 轮廓系数的范围可以是 -1 到 1，但在这个例子中，所有值都在 [-0.1, 1] 之间
    ax1.set_xlim([-0.1, 1])
    # (n_clusters+1)*10 是为了在各个簇的轮廓图之间插入空白，以便清晰地将它们分开。
    ax1.set_ylim([0, len(X) + (n_clusters + 1) * 10])

    # 初始化聚类器时，设置 n_clusters 值，并使用随机生成器种子 10 以确保结果可重复。
    clusterer = KMeans(n_clusters=n_clusters, random_state=10)
    cluster_labels = clusterer.fit_predict(X)

    # 轮廓系数（silhouette_score）为所有样本提供了一个平均值。这提供了对形成的聚类的密度和分离度的一个视角。
    silhouette_avg = silhouette_score(X, cluster_labels)
    print(
        "For n_clusters =",
        n_clusters,
        "The average silhouette_score is :",
        silhouette_avg,
    )

    # 计算每个样本的轮廓系数
    sample_silhouette_values = silhouette_samples(X, cluster_labels)

    y_lower = 10
    for i in range(n_clusters):
        # 汇总属于第 i 个簇的样本的轮廓系数，并对它们进行排序。
        ith_cluster_silhouette_values = sample_silhouette_values[cluster_labels == i]

        ith_cluster_silhouette_values.sort()

        size_cluster_i = ith_cluster_silhouette_values.shape[0]
        y_upper = y_lower + size_cluster_i

        color = cm.nipy_spectral(float(i) / n_clusters)
        ax1.fill_betweenx(
            np.arange(y_lower, y_upper),
            0,
            ith_cluster_silhouette_values,
            facecolor=color,
            edgecolor=color,
            alpha=0.7,
        )

        # 在轮廓图的中间标注其簇编号
        ax1.text(-0.05, y_lower + 0.5 * size_cluster_i, str(i))

        # 计算下一个图的新的 y_lower
        y_lower = y_upper + 10  # 10 for the 0 samples

    ax1.set_title("The silhouette plot for the various clusters.")
    ax1.set_xlabel("The silhouette coefficient values")
    ax1.set_ylabel("Cluster label")

    # 所有值的平均轮廓分数的垂直线
    ax1.axvline(x=silhouette_avg, color="red", linestyle="--")

    ax1.set_yticks([])  # Clear the yaxis labels / ticks
    ax1.set_xticks([-0.1, 0, 0.2, 0.4, 0.6, 0.8, 1])

    # 第二个图显示了实际形成的簇群
    colors = cm.nipy_spectral(cluster_labels.astype(float) / n_clusters)
    ax2.scatter(
        X[:, 0], X[:, 1], marker=".", s=30, lw=0, alpha=0.7, c=colors, edgecolor="k"
    )

    # 标记簇群
    centers = clusterer.cluster_centers_
    # 在聚类中心绘制白色圆圈
    ax2.scatter(
        centers[:, 0],
        centers[:, 1],
        marker="o",
        c="white",
        alpha=1,
        s=200,
        edgecolor="k",
    )

    for i, c in enumerate(centers):
        ax2.scatter(c[0], c[1], marker="$%d$" % i, alpha=1, s=50, edgecolor="k")

    ax2.set_title("The visualization of the clustered data.")
    ax2.set_xlabel("Feature space for the 1st feature")
    ax2.set_ylabel("Feature space for the 2nd feature")

    plt.suptitle(
        "Silhouette analysis for KMeans clustering on sample data with n_clusters = %d"
        % n_clusters,
        fontsize=14,
        fontweight="bold",
    )

plt.show()