Note
Go to the end to download the full example code. or to run this example in your browser via Binder
收缩协方差估计:LedoitWolf vs OAS 和最大似然#
在进行协方差估计时,通常的方法是使用最大似然估计器,例如
EmpiricalCovariance 。它是无偏的,即当给定大量观测值时,它会收敛到真实的(总体)协方差。然而,正则化它也可能是有益的,以减少其方差;这反过来会引入一些偏差。本示例说明了在
收缩协方差 估计器中使用的简单正则化。特别是,它重点介绍了如何设置正则化的量,即如何选择偏差-方差权衡。
生成示例数据#
import numpy as np
n_features, n_samples = 40, 20
np.random.seed(42)
base_X_train = np.random.normal(size=(n_samples, n_features))
base_X_test = np.random.normal(size=(n_samples, n_features))
# 颜色样本
coloring_matrix = np.random.normal(size=(n_features, n_features))
X_train = np.dot(base_X_train, coloring_matrix)
X_test = np.dot(base_X_test, coloring_matrix)
计算测试数据的似然度#
from scipy import linalg
from sklearn.covariance import ShrunkCovariance, empirical_covariance, log_likelihood
# 跨越一系列可能的收缩系数值
shrinkages = np.logspace(-2, 0, 30)
negative_logliks = [
-ShrunkCovariance(shrinkage=s).fit(X_train).score(X_test) for s in shrinkages
]
# 在真实环境中,我们无法访问的真实模型下
real_cov = np.dot(coloring_matrix.T, coloring_matrix)
emp_cov = empirical_covariance(X_train)
loglik_real = -log_likelihood(emp_cov, linalg.inv(real_cov))
比较设置正则化参数的不同方法#
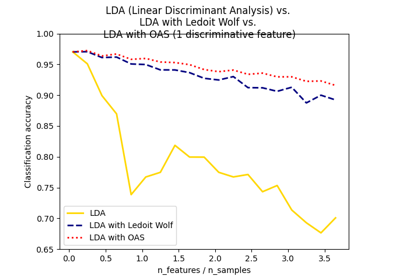
这里我们比较了三种方法:
通过在三个折叠上交叉验证似然,根据潜在收缩参数的网格设置参数。
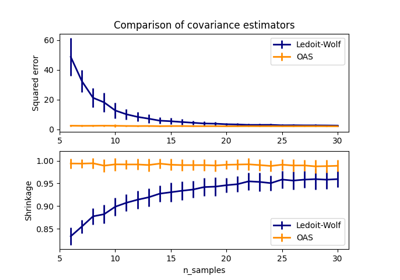
Ledoit 和 Wolf 提出的一个封闭公式,用于计算渐近最优正则化参数(最小化均方误差准则),从而得出
LedoitWolf协方差估计。Ledoit-Wolf 收缩的改进版,由 Chen 等人提出的
OAS。在假设数据为高斯分布的情况下,其收敛性显著更好,特别是对于小样本。
from sklearn.covariance import OAS, LedoitWolf
from sklearn.model_selection import GridSearchCV
# 网格搜索最优收缩系数
tuned_parameters = [{"shrinkage": shrinkages}]
cv = GridSearchCV(ShrunkCovariance(), tuned_parameters)
cv.fit(X_train)
# Ledoit-Wolf 最优收缩系数估计
lw = LedoitWolf()
loglik_lw = lw.fit(X_train).score(X_test)
# OAS 系数估计
oa = OAS()
loglik_oa = oa.fit(X_train).score(X_test)
绘制结果#
为了量化估计误差,我们绘制了在不同收缩参数值下未见数据的似然性图。我们还展示了通过交叉验证、LedoitWolf 和 OAS 估计方法所做的选择。
import matplotlib.pyplot as plt
fig = plt.figure()
plt.title("Regularized covariance: likelihood and shrinkage coefficient")
plt.xlabel("Regularization parameter: shrinkage coefficient")
plt.ylabel("Error: negative log-likelihood on test data")
# 范围收缩曲线
plt.loglog(shrinkages, negative_logliks, label="Negative log-likelihood")
plt.plot(plt.xlim(), 2 * [loglik_real], "--r", label="Real covariance likelihood")
# adjust view
lik_max = np.amax(negative_logliks)
lik_min = np.amin(negative_logliks)
ymin = lik_min - 6.0 * np.log((plt.ylim()[1] - plt.ylim()[0]))
ymax = lik_max + 10.0 * np.log(lik_max - lik_min)
xmin = shrinkages[0]
xmax = shrinkages[-1]
# LW 可能性
plt.vlines(
lw.shrinkage_,
ymin,
-loglik_lw,
color="magenta",
linewidth=3,
label="Ledoit-Wolf estimate",
)
# OAS 可能性
plt.vlines(
oa.shrinkage_, ymin, -loglik_oa, color="purple", linewidth=3, label="OAS estimate"
)
# 最佳CV估计器似然
plt.vlines(
cv.best_estimator_.shrinkage,
ymin,
-cv.best_estimator_.score(X_test),
color="cyan",
linewidth=3,
label="Cross-validation best estimate",
)
plt.ylim(ymin, ymax)
plt.xlim(xmin, xmax)
plt.legend()
plt.show()
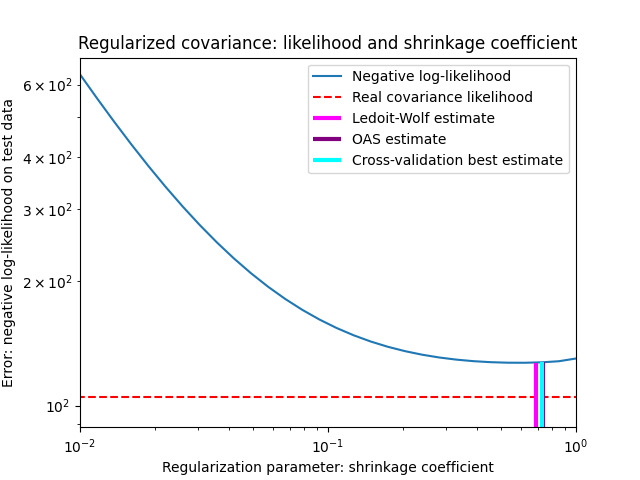
最大似然估计对应于无收缩,因此表现较差。Ledoit-Wolf估计表现非常好,因为它接近最优且计算成本不高。在这个例子中,OAS估计稍微差一些。有趣的是,这两种方法都优于交叉验证,而交叉验证的计算成本显著更高。
Total running time of the script: (0 minutes 0.186 seconds)
Related examples