Note

Go to the end to download the full example code. or to run this example in your browser via Binder

使用k-means聚类文本文档#

这是一个展示如何使用scikit-learn API通过 词袋模型 来按主题聚类文档的示例。

展示了两种算法，即 KMeans 及其更具可扩展性的变体 MiniBatchKMeans 。此外，还使用潜在语义分析来降低维度并发现数据中的潜在模式。

此示例使用了两种不同的文本向量化器：TfidfVectorizer 和 HashingVectorizer 。有关向量化器的更多信息及其处理时间的比较，请参见示例笔记本 特征哈希器和字典向量化器比较 。

对于通过监督学习方法进行的文档分析，请参见示例脚本 使用稀疏特征对文本文档进行分类 。

# 作者：scikit-learn 开发者
# SPDX许可证标识符：BSD-3-Clause

加载文本数据#

我们从 The 20 newsgroups text dataset 加载数据，该数据集包含大约 18,000 篇关于 20 个主题的新闻组帖子。为了说明目的并减少计算成本，我们仅选择了 4 个主题的子集，大约包含 3,400 篇文档。请参阅示例 使用稀疏特征对文本文档进行分类 以了解这些主题的重叠情况。

请注意，默认情况下，文本样本包含一些消息元数据，例如“headers”、“footers”（签名）和对其他帖子引用的“quotes”。我们使用 fetch_20newsgroups 的 remove 参数来去除这些特征，从而使聚类问题更加合理。

import numpy as np

from sklearn.datasets import fetch_20newsgroups

categories = [
    "alt.atheism",
    "talk.religion.misc",
    "comp.graphics",
    "sci.space",
]

dataset = fetch_20newsgroups(
    remove=("headers", "footers", "quotes"),
    subset="all",
    categories=categories,
    shuffle=True,
    random_state=42,
)

labels = dataset.target
unique_labels, category_sizes = np.unique(labels, return_counts=True)
true_k = unique_labels.shape[0]

print(f"{len(dataset.data)} documents - {true_k} categories")

3387 documents - 4 categories

量化聚类结果的质量#

在本节中，我们定义了一个函数，使用多种指标对不同的聚类管道进行评分。

聚类算法本质上是无监督学习方法。然而，由于我们恰好拥有这个特定数据集的类别标签，因此可以使用利用这种“监督”真实信息的评估指标来量化生成簇的质量。此类指标的示例如下：

  • 同质性，量化集群中仅包含单个类别成员的程度；

  • 完整性，量化给定类别的成员有多少被分配到相同的簇中；

  • V-measure，完整性和同质性的调和平均值；

  • 兰德指数，衡量数据点对根据聚类算法结果和真实类别分配的一致分组频率；

  • 调整兰德指数，一种经过机会调整的兰德指数，使得随机聚类分配的期望ARI为0.0。

如果不知道真实标签，只能使用模型结果进行评估。在这种情况下，轮廓系数非常有用。有关如何执行此操作的示例，请参见 使用轮廓分析选择KMeans聚类的簇数 。

如需更多参考，请参见 clustering_evaluation .

from collections import defaultdict
from time import time

from sklearn import metrics

evaluations = []
evaluations_std = []


def fit_and_evaluate(km, X, name=None, n_runs=5):
    name = km.__class__.__name__ if name is None else name

    train_times = []
    scores = defaultdict(list)
    for seed in range(n_runs):
        km.set_params(random_state=seed)
        t0 = time()
        km.fit(X)
        train_times.append(time() - t0)
        scores["Homogeneity"].append(metrics.homogeneity_score(labels, km.labels_))
        scores["Completeness"].append(metrics.completeness_score(labels, km.labels_))
        scores["V-measure"].append(metrics.v_measure_score(labels, km.labels_))
        scores["Adjusted Rand-Index"].append(
            metrics.adjusted_rand_score(labels, km.labels_)
        )
        scores["Silhouette Coefficient"].append(
            metrics.silhouette_score(X, km.labels_, sample_size=2000)
        )
    train_times = np.asarray(train_times)

    print(f"clustering done in {train_times.mean():.2f} ± {train_times.std():.2f} s ")
    evaluation = {
        "estimator": name,
        "train_time": train_times.mean(),
    }
    evaluation_std = {
        "estimator": name,
        "train_time": train_times.std(),
    }
    for score_name, score_values in scores.items():
        mean_score, std_score = np.mean(score_values), np.std(score_values)
        print(f"{score_name}: {mean_score:.3f} ± {std_score:.3f}")
        evaluation[score_name] = mean_score
        evaluation_std[score_name] = std_score
    evaluations.append(evaluation)
    evaluations_std.append(evaluation_std)

K-means 聚类文本特征#

在这个例子中使用了两种特征提取方法：

  • TfidfVectorizer 使用内存中的词汇表（一个 Python 字典）将最常见的单词映射到特征索引，从而计算单词出现频率（稀疏）矩阵。然后使用在整个语料库中按特征收集的逆文档频率（IDF）向量重新加权单词频率。

  • HashingVectorizer 将词语出现次数哈希到一个固定的维度空间，可能会发生冲突。然后将词频向量归一化，使每个向量的 l2 范数等于 1（投影到欧几里得单位球面），这对于 k-means 在高维空间中工作似乎很重要。

此外，可以使用降维对提取的特征进行后处理。我们将在下文中探讨这些选择对聚类质量的影响。

使用TfidfVectorizer进行特征提取#

我们首先使用字典向量化器以及由:class:~sklearn.feature_extraction.text.TfidfVectorizer 提供的IDF归一化对估计器进行基准测试。

from sklearn.feature_extraction.text import TfidfVectorizer

vectorizer = TfidfVectorizer(
    max_df=0.5,
    min_df=5,
    stop_words="english",
)
t0 = time()
X_tfidf = vectorizer.fit_transform(dataset.data)

print(f"vectorization done in {time() - t0:.3f} s")
print(f"n_samples: {X_tfidf.shape[0]}, n_features: {X_tfidf.shape[1]}")

vectorization done in 0.223 s
n_samples: 3387, n_features: 7929

在忽略出现在超过50%文档中的词项（由 max_df=0.5 设置）和在至少5个文档中未出现的词项（由 min_df=5 设置）后，得到的唯一词项数 n_features 大约是8,000。我们还可以通过非零条目占总元素的比例来量化 X_tfidf 矩阵的稀疏性。

print(f"{X_tfidf.nnz / np.prod(X_tfidf.shape):.3f}")

0.007

我们发现 X_tfidf 矩阵中约有 0.7% 的条目是非零的。

使用k-means对稀疏数据进行聚类#

由于 KMeans 和 MiniBatchKMeans 都优化非凸目标函数，它们的聚类结果不能保证对于给定的随机初始化是最优的。更进一步地，对于使用词袋方法向量化的稀疏高维数据（如文本），k-means 可能会在极其孤立的数据点上初始化质心。这些数据点可能会始终保持为它们自己的质心。

以下代码说明了在某些情况下，取决于随机初始化，前述现象如何导致高度不平衡的聚类：

from sklearn.cluster import KMeans

for seed in range(5):
    kmeans = KMeans(
        n_clusters=true_k,
        max_iter=100,
        n_init=1,
        random_state=seed,
    ).fit(X_tfidf)
    cluster_ids, cluster_sizes = np.unique(kmeans.labels_, return_counts=True)
    print(f"Number of elements assigned to each cluster: {cluster_sizes}")
print()
print(
    "True number of documents in each category according to the class labels: "
    f"{category_sizes}"
)

Number of elements assigned to each cluster: [ 481  675 1785  446]
Number of elements assigned to each cluster: [ 575  619  485 1708]
Number of elements assigned to each cluster: [   1    1    1 3384]
Number of elements assigned to each cluster: [1887  311  332  857]
Number of elements assigned to each cluster: [ 291  673 1771  652]

True number of documents in each category according to the class labels: [799 973 987 628]

为了避免这个问题，一种可能性是增加具有独立随机初始化的运行次数 n_init 。在这种情况下，选择具有最佳惯性（k-means 的目标函数）的聚类。

kmeans = KMeans(
    n_clusters=true_k,
    max_iter=100,
    n_init=5,
)

fit_and_evaluate(kmeans, X_tfidf, name="KMeans\non tf-idf vectors")

clustering done in 0.27 ± 0.08 s
Homogeneity: 0.353 ± 0.010
Completeness: 0.404 ± 0.006
V-measure: 0.377 ± 0.008
Adjusted Rand-Index: 0.235 ± 0.056
Silhouette Coefficient: 0.007 ± 0.001

所有这些聚类评估指标的最大值为1.0（对于完美的聚类结果）。值越高越好。接近0.0的调整兰德指数值对应于随机标记。从上面的分数可以看出，聚类分配确实远高于随机水平，但整体质量肯定可以提高。

请注意，类标签可能无法准确反映文档主题，因此使用标签的指标不一定是评估聚类管道质量的最佳方法。

使用 LSA 进行降维#

n_init=1 仍然可以使用，只要首先减少向量化空间的维度以使 k-means 更加稳定。为此，我们使用 TruncatedSVD ，它适用于词频/TF-IDF 矩阵。由于 SVD 结果未归一化，我们重新进行归一化以改进 KMeans 的结果。使用 SVD 降低 TF-IDF 文档向量的维度在信息检索和文本挖掘文献中通常被称为 潜在语义分析 (LSA)。

from sklearn.decomposition import TruncatedSVD
from sklearn.pipeline import make_pipeline
from sklearn.preprocessing import Normalizer

lsa = make_pipeline(TruncatedSVD(n_components=100), Normalizer(copy=False))
t0 = time()
X_lsa = lsa.fit_transform(X_tfidf)
explained_variance = lsa[0].explained_variance_ratio_.sum()

print(f"LSA done in {time() - t0:.3f} s")
print(f"Explained variance of the SVD step: {explained_variance * 100:.1f}%")

LSA done in 0.249 s
Explained variance of the SVD step: 18.4%

使用单次初始化意味着 KMeans 和 MiniBatchKMeans 的处理时间将会减少。

kmeans = KMeans(
    n_clusters=true_k,
    max_iter=100,
    n_init=1,
)

fit_and_evaluate(kmeans, X_lsa, name="KMeans\nwith LSA on tf-idf vectors")

clustering done in 0.05 ± 0.01 s
Homogeneity: 0.404 ± 0.009
Completeness: 0.440 ± 0.016
V-measure: 0.421 ± 0.010
Adjusted Rand-Index: 0.322 ± 0.022
Silhouette Coefficient: 0.032 ± 0.002

我们可以观察到，对文档的LSA表示进行聚类的速度显著更快（既因为 n_init=1 ，也因为LSA特征空间的维度要小得多）。此外，所有的聚类评估指标都有所改善。我们使用:class:~sklearn.cluster.MiniBatchKMeans 重复实验。

from sklearn.cluster import MiniBatchKMeans

minibatch_kmeans = MiniBatchKMeans(
    n_clusters=true_k,
    n_init=1,
    init_size=1000,
    batch_size=1000,
)

fit_and_evaluate(
    minibatch_kmeans,
    X_lsa,
    name="MiniBatchKMeans\nwith LSA on tf-idf vectors",
)

clustering done in 0.08 ± 0.01 s
Homogeneity: 0.268 ± 0.110
Completeness: 0.339 ± 0.051
V-measure: 0.294 ± 0.089
Adjusted Rand-Index: 0.204 ± 0.128
Silhouette Coefficient: 0.023 ± 0.005

每个聚类的主要术语#

由于 TfidfVectorizer 可以被反转，我们可以识别出聚类中心，这为每个聚类中最具影响力的词提供了直观的理解。请参阅示例脚本 使用稀疏特征对文本文档进行分类 ，以比较每个目标类别中最具预测性的词。

original_space_centroids = lsa[0].inverse_transform(kmeans.cluster_centers_)
order_centroids = original_space_centroids.argsort()[ :, ::-1]
terms = vectorizer.get_feature_names_out()

for i in range(true_k):
    print(f"Cluster {i}: ", end="")
    for ind in order_centroids[i, :10]:
        print(f"{terms[ind]} ", end="")
    print()

Cluster 0: god people don think just say know like does believe
Cluster 1: space launch orbit like earth shuttle moon nasa just cost
Cluster 2: thanks files file know format program advance help gif hi
Cluster 3: graphics edu image computer software code mail 3d use data

哈希向量化器#

另一种向量化方法是使用 HashingVectorizer 实例，该实例不提供 IDF 加权，因为这是一个无状态模型（fit 方法不起作用）。当需要 IDF 加权时，可以通过将 HashingVectorizer 的输出传递给 TfidfTransformer 实例来添加。在这种情况下，我们还将 LSA 添加到管道中，以减少哈希向量空间的维度和稀疏性。

from sklearn.feature_extraction.text import HashingVectorizer, TfidfTransformer

lsa_vectorizer = make_pipeline(
    HashingVectorizer(stop_words="english", n_features=50_000),
    TfidfTransformer(),
    TruncatedSVD(n_components=100, random_state=0),
    Normalizer(copy=False),
)

t0 = time()
X_hashed_lsa = lsa_vectorizer.fit_transform(dataset.data)
print(f"vectorization done in {time() - t0:.3f} s")

vectorization done in 1.032 s

可以观察到，LSA 步骤需要相对较长的时间来拟合，尤其是使用哈希向量时。原因是哈希空间通常很大（在此示例中设置为 n_features=50_000 ）。可以尝试降低特征数量，但代价是具有哈希冲突的特征比例会更大，如示例笔记本 特征哈希器和字典向量化器比较 所示。

我们现在在这个哈希-LSA-降维后的数据上拟合并评估 kmeans 和 minibatch_kmeans 实例：

fit_and_evaluate(kmeans, X_hashed_lsa, name="KMeans\nwith LSA on hashed vectors")

clustering done in 0.07 ± 0.03 s
Homogeneity: 0.398 ± 0.009
Completeness: 0.447 ± 0.015
V-measure: 0.421 ± 0.011
Adjusted Rand-Index: 0.324 ± 0.012
Silhouette Coefficient: 0.030 ± 0.002

fit_and_evaluate(
    minibatch_kmeans,
    X_hashed_lsa,
    name="MiniBatchKMeans\nwith LSA on hashed vectors",
)

clustering done in 0.07 ± 0.01 s
Homogeneity: 0.344 ± 0.057
Completeness: 0.366 ± 0.061
V-measure: 0.354 ± 0.059
Adjusted Rand-Index: 0.303 ± 0.054
Silhouette Coefficient: 0.029 ± 0.002

两种方法都能产生良好的结果，类似于在传统的LSA向量（不使用哈希）上运行相同的模型。

聚类评估摘要#

import matplotlib.pyplot as plt
import pandas as pd

fig, (ax0, ax1) = plt.subplots(ncols=2, figsize=(16, 6), sharey=True)

df = pd.DataFrame(evaluations[::-1]).set_index("estimator")
df_std = pd.DataFrame(evaluations_std[::-1]).set_index("estimator")

df.drop(
    ["train_time"],
    axis="columns",
).plot.barh(ax=ax0, xerr=df_std)
ax0.set_xlabel("Clustering scores")
ax0.set_ylabel("")

df["train_time"].plot.barh(ax=ax1, xerr=df_std["train_time"])
ax1.set_xlabel("Clustering time (s)")
plt.tight_layout()
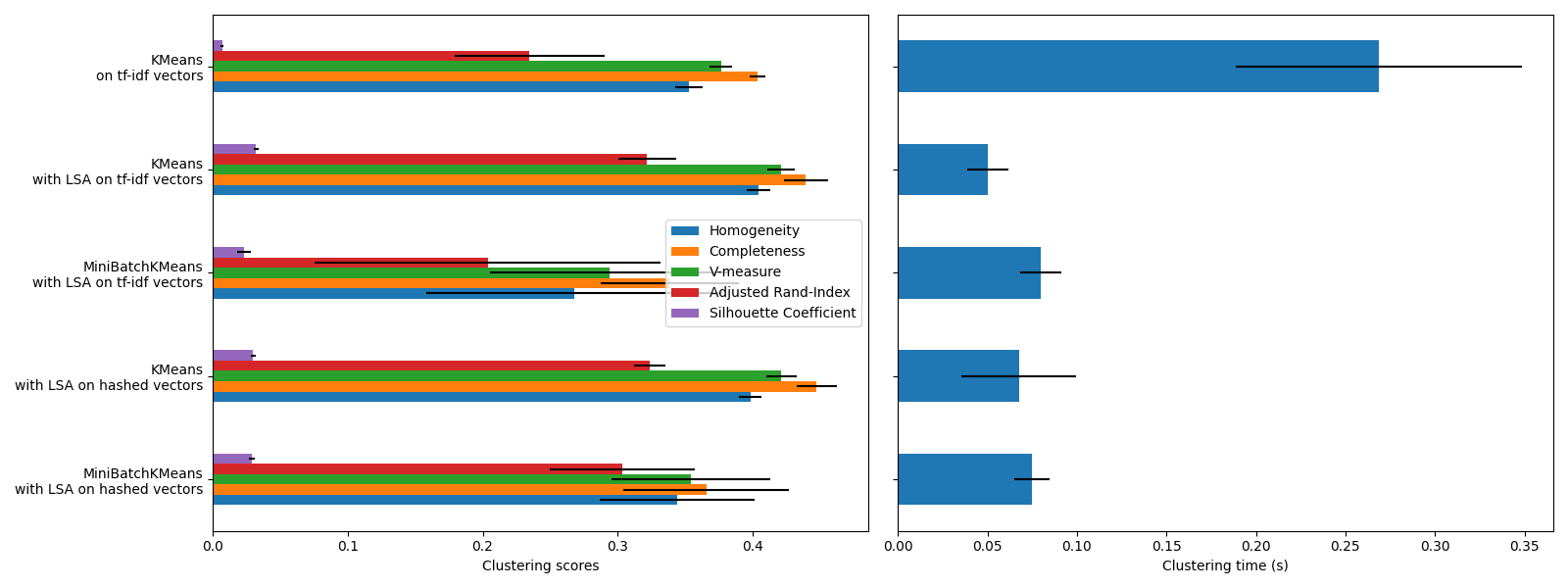
plot document clustering

KMeans 和 MiniBatchKMeans 在处理高维数据集（如文本数据）时会遭遇所谓的“维度诅咒 <https://en.wikipedia.org/wiki/Curse_of_dimensionality> `_ 现象。这就是为什么使用 LSA 后整体得分会提高的原因。使用 LSA 降维后的数据还可以提高稳定性并减少聚类时间，但请记住，LSA 步骤本身需要很长时间，尤其是对于哈希向量。

轮廓系数的定义在0到1之间。在所有情况下，我们得到的值都接近0（即使在使用LSA后有所改善），因为它的定义需要测量距离，这与其他评估指标（如V-measure和调整兰德指数）不同，后者仅基于聚类分配而不是距离。请注意，严格来说，不应在不同维度的空间之间比较轮廓系数，因为它们暗示了不同的距离概念。

同质性、完整性以及 v-measure 指标在随机标记方面不会产生基线：这意味着根据样本数量、聚类数量和真实类别，完全随机的标记不会总是产生相同的值。特别是，随机标记不会产生零分，尤其是在聚类数量较多时。当样本数量超过一千且聚类数量少于 10 时，这个问题可以忽略不计，这也是当前示例的情况。对于较小的样本量或较多的聚类数量，使用调整后的指数（如调整兰德指数，ARI）会更安全。请参阅示例 :ref:` sphx_glr_auto_examples_cluster_plot_adjusted_for_chance_measures.py `了解随机标记效果的演示。

误差条的大小表明，对于这个相对较小的数据集，:class:` ~sklearn.cluster.MiniBatchKMeans 比 :class: ~sklearn.cluster.KMeans`稳定性更差。当样本数量大得多时，使用它会更有趣，但与传统的k-means算法相比，可能会在聚类质量上有小幅下降。

Total running time of the script: (0 minutes 6.728 seconds)

Launch binder

Download Jupyter notebook: plot_document_clustering.ipynb

Download Python source code: plot_document_clustering.py

Download zipped: plot_document_clustering.zip

Related examples

手写数字数据上的K-Means聚类演示

手写数字数据上的K-Means聚类演示

K-Means 和 MiniBatchKMeans 聚类算法的比较

K-Means 和 MiniBatchKMeans 聚类算法的比较

k-means 初始化影响的经验评估

k-means 初始化影响的经验评估

使用谱协同聚类算法对文档进行双聚类

使用谱协同聚类算法对文档进行双聚类

Gallery generated by Sphinx-Gallery

On this page
Show Source