Note

Go to the end to download the full example code. or to run this example in your browser via Binder

分类器校准比较#

校准良好的分类器是概率分类器，其输出的 predict_proba 可以直接解释为置信水平。例如，一个校准良好的（二元）分类器应当对样本进行分类，使得对于其给出 predict_proba 值接近 0.8 的样本，约 80% 实际上属于正类。

在这个例子中，我们将比较四种不同模型的校准情况：逻辑回归、高斯朴素贝叶斯、Random Forest Classifier 和 Linear SVM 。

作者：scikit-learn 开发者 SPDX-License-Identifier: BSD-3-Clause

Dataset#

我们将使用一个包含100,000个样本和20个特征的合成二元分类数据集。在这20个特征中，只有2个是信息性的，2个是冗余的（信息性特征的随机组合），其余16个是无信息性的（随机数）。

在100,000个样本中，100个将用于模型拟合，其余的用于测试。请注意，这种划分相当不寻常：其目的是为可能容易过拟合的模型获得稳定的校准曲线估计。在实际操作中，应该使用更平衡的划分进行交叉验证，但这会使本示例的代码更难以理解。

from sklearn.datasets import make_classification
from sklearn.model_selection import train_test_split

X, y = make_classification(
    n_samples=100_000, n_features=20, n_informative=2, n_redundant=2, random_state=42
)

train_samples = 100  # Samples used for training the models
X_train, X_test, y_train, y_test = train_test_split(
    X,
    y,
    shuffle=False,
    test_size=100_000 - train_samples,
)

校准曲线#

下面，我们使用小型训练数据集训练四个模型中的每一个，然后使用测试数据集的预测概率绘制校准曲线（也称为可靠性图）。校准曲线是通过对预测概率进行分箱，然后将每个箱中的平均预测概率与观察到的频率（“正样本比例”）进行绘图来创建的。在校准曲线下方，我们绘制一个直方图，显示预测概率的分布，更具体地说，是每个预测概率箱中的样本数量。

import numpy as np

from sklearn.svm import LinearSVC


class NaivelyCalibratedLinearSVC(LinearSVC):
    """带有 `predict_proba` 方法的 LinearSVC，简单地缩放 `decision_function` 输出。"""

    def fit(self, X, y):
        super().fit(X, y)
        df = self.decision_function(X)
        self.df_min_ = df.min()
        self.df_max_ = df.max()

    def predict_proba(self, X):
        """将 `decision_function` 的输出按最小-最大比例缩放到 [0,1]。"""
        df = self.decision_function(X)
        calibrated_df = (df - self.df_min_) / (self.df_max_ - self.df_min_)
        proba_pos_class = np.clip(calibrated_df, 0, 1)
        proba_neg_class = 1 - proba_pos_class
        proba = np.c_[proba_neg_class, proba_pos_class]
        return proba

from sklearn.calibration import CalibrationDisplay
from sklearn.ensemble import RandomForestClassifier
from sklearn.linear_model import LogisticRegressionCV
from sklearn.naive_bayes import GaussianNB

# 定义在研究中要比较的分类器。
#
# 请注意，我们使用了一种可以自动调整其正则化参数的逻辑回归模型变体。
#
# 为了公平比较，我们应该对所有分类器进行超参数搜索，但为了保持示例代码简洁和快速执行，我们在这里不进行超参数搜索。
lr = LogisticRegressionCV(
    Cs=np.logspace(-6, 6, 101), cv=10, scoring="neg_log_loss", max_iter=1_000
)
gnb = GaussianNB()
svc = NaivelyCalibratedLinearSVC(C=1.0)
rfc = RandomForestClassifier(random_state=42)

clf_list = [
    (lr, "Logistic Regression"),
    (gnb, "Naive Bayes"),
    (svc, "SVC"),
    (rfc, "Random forest"),
]

import matplotlib.pyplot as plt
from matplotlib.gridspec import GridSpec

fig = plt.figure(figsize=(10, 10))
gs = GridSpec(4, 2)
colors = plt.get_cmap("Dark2")

ax_calibration_curve = fig.add_subplot(gs[:2, :2])
calibration_displays = {}
markers = ["^", "v", "s", "o"]
for i, (clf, name) in enumerate(clf_list):
    clf.fit(X_train, y_train)
    display = CalibrationDisplay.from_estimator(
        clf,
        X_test,
        y_test,
        n_bins=10,
        name=name,
        ax=ax_calibration_curve,
        color=colors(i),
        marker=markers[i],
    )
    calibration_displays[name] = display

ax_calibration_curve.grid()
ax_calibration_curve.set_title("Calibration plots")

# 添加直方图
grid_positions = [(2, 0), (2, 1), (3, 0), (3, 1)]
for i, (_, name) in enumerate(clf_list):
    row, col = grid_positions[i]
    ax = fig.add_subplot(gs[row, col])

    ax.hist(
        calibration_displays[name].y_prob,
        range=(0, 1),
        bins=10,
        label=name,
        color=colors(i),
    )
    ax.set(title=name, xlabel="Mean predicted probability", ylabel="Count")

plt.tight_layout()
plt.show()

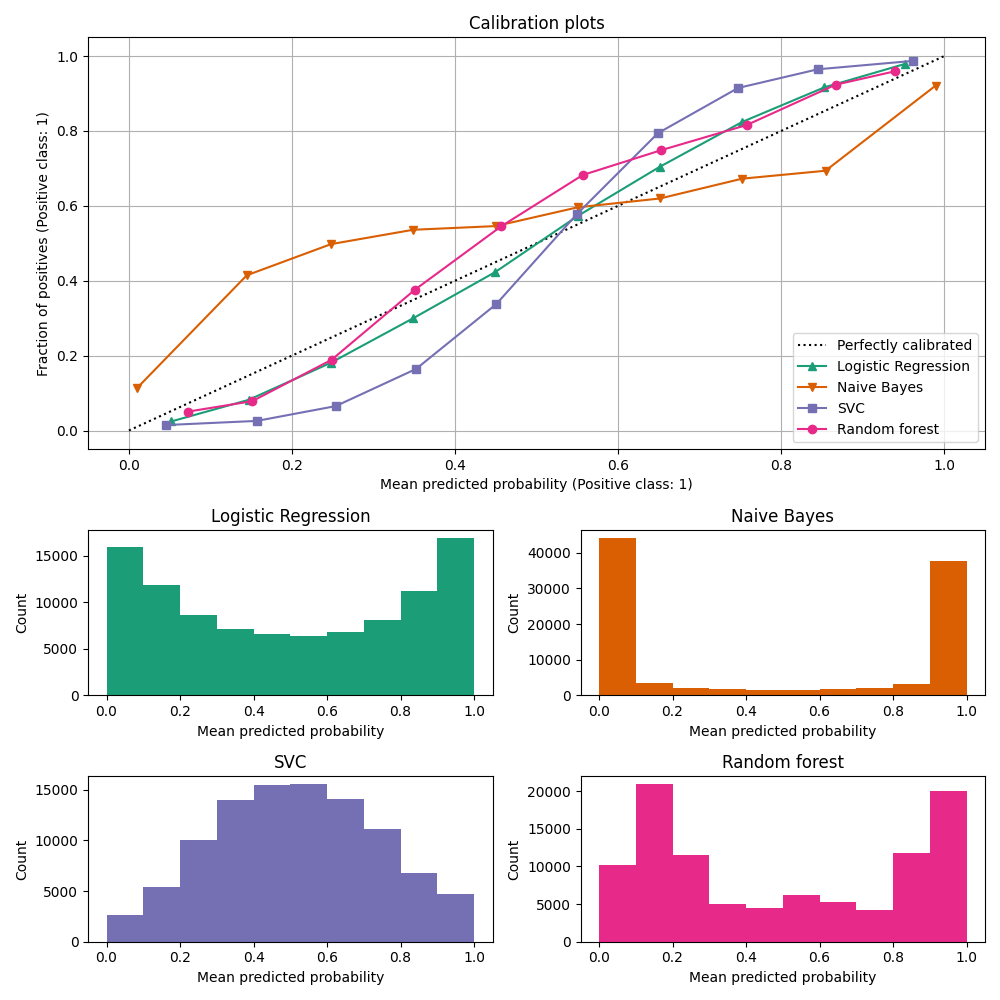
Calibration plots, Logistic Regression, Naive Bayes, SVC, Random forest

结果分析#

LogisticRegressionCV 尽管训练集规模较小，仍能返回相当准确的预测结果：在四个模型中，其可靠性曲线最接近对角线。

逻辑回归通过最小化对数损失进行训练，对数损失是一种严格的适当评分规则：在无限训练数据的情况下，严格的适当评分规则会被预测真实条件概率的模型最小化。因此，该（假设的）模型将会完全校准。然而，仅使用适当的评分规则作为训练目标并不足以保证模型本身良好校准：即使有一个非常大的训练集，如果正则化过强，或者输入特征的选择和预处理使得该模型错误指定（例如，如果数据集的真实决策边界是输入特征的高度非线性函数），逻辑回归仍可能校准不佳。

在这个例子中，训练集被故意保持得非常小。在这种情况下，优化对数损失仍然可能导致模型校准不佳，因为过拟合。为了缓解这一问题，LogisticRegressionCV 类被配置为通过内部交叉验证调整 C 正则化参数，以最小化对数损失，从而在小训练集设置中找到该模型的最佳折衷方案。

由于训练集规模有限且无法保证良好的规范性，我们观察到逻辑回归模型的校准曲线接近但不完全在对角线上。该模型的校准曲线形状可以解释为略微不够自信：预测概率相比于正样本的真实比例稍微过于接近0.5。

其他方法输出的概率校准效果都不如这个好：

GaussianNB 倾向于在这个特定数据集上将概率推向0或1（见直方图）（过度自信）。这主要是因为朴素贝叶斯方程仅在特征条件独立的假设成立时才能提供正确的概率估计 [2]。然而，特征可能是相关的，而在这个数据集中确实如此，其中包含的两个特征是通过信息特征的随机线性组合生成的。这些相关特征实际上被“计算了两次”，导致预测概率被推向0和1 [3]。但是请注意，更改用于生成数据集的种子可能会导致朴素贝叶斯估计器的结果有很大差异。
LinearSVC 不是一个天然的概率分类器。为了将其预测解释为概率，我们在上面定义的 NaivelyCalibratedLinearSVC 包装类中，通过应用最小-最大缩放将 decision_function 的输出天真地缩放到 [0, 1]。在此数据上，该估计器显示出典型的 S 型校准曲线：大于 0.5 的预测对应于具有更大有效正类比例的样本（在对角线上方），而小于 0.5 的预测对应于更低的正类比例（在对角线下方）。这种不自信的预测是最大边距方法的典型特征 [1]。
RandomForestClassifier 的预测直方图在大约 0.2 和 0.9 概率处显示出峰值，而接近 0 或 1 的概率则非常罕见。对此的解释见 [1]：

“诸如 bagging 和随机森林等方法通过对一组基础模型的预测进行平均，可能难以在接近 0 和 1 的地方做出预测，因为基础模型的方差会使应该接近零或一的预测偏离这些值。由于预测被限制在 [0, 1] 区间内，方差引起的错误在接近零和一时往往是单方面的。例如，如果一个模型应该为某个案例预测 p = 0，那么 bagging 唯一能实现这一点的方法是所有 bagged 树都预测为零。如果我们向 bagging 所平均的树中添加噪声，这些噪声会导致一些树为该案例预测大于 0 的值，从而将 bagged 集成的平均预测值从 0 移开。我们在随机森林中最强烈地观察到这一效应，因为随机森林训练的基础级树由于特征子集化而具有相对较高的方差。” 这种效应可能会使随机森林信心不足。尽管存在这种可能的偏差，请注意树本身是通过最小化 Gini 或 Entropy 标准来拟合的，这两者都会导致分裂最小化适当的评分规则：分别是 Brier 分数或对数损失。有关更多详细信息，请参见用户指南。这可以解释为什么该模型在这个特定示例数据集上显示出足够好的校准曲线。实际上，随机森林模型并不比逻辑回归模型显著更缺乏信心。

请随意使用不同的随机种子和其他数据集生成参数重新运行此示例，以查看校准图的不同表现。一般来说，逻辑回归和随机森林往往是校准最好的分类器，而SVC通常会显示典型的低置信度失校准。朴素贝叶斯模型也常常校准较差，但其校准曲线的总体形状可能会因数据集的不同而有很大差异。

请注意，对于某些数据集种子，即使按照上述方法调整正则化参数，所有模型的校准效果仍然很差。当训练集规模过小时或模型严重设定错误时，这种情况是不可避免的。

References#

<https://dl.acm.org/doi/pdf/10.1145/1102351.1102430>`_ , A. Niculescu-Mizil 和 R. Caruana, ICML 2005

<https://www.ics.uci.edu/~pazzani/Publications/mlc96-pedro.pdf>`_ Domingos, P., & Pazzani, M., 第13届国际机器学习会议论文集. 1996.

<https://citeseerx.ist.psu.edu/doc_view/pid/4f67a122ec3723f08ad5cbefecad119b432b3304>`_ Zadrozny, Bianca, 和 Charles Elkan. Icml. 第1卷. 2001.

Total running time of the script: (0 minutes 1.140 seconds)

Related examples

概率校准曲线

归纳聚类

__sklearn_is_fitted__ 作为开发者 API

离散数据结构上的高斯过程

Gallery generated by Sphinx-Gallery