TemporalNorm

%load_ext autoreload
%autoreload 2

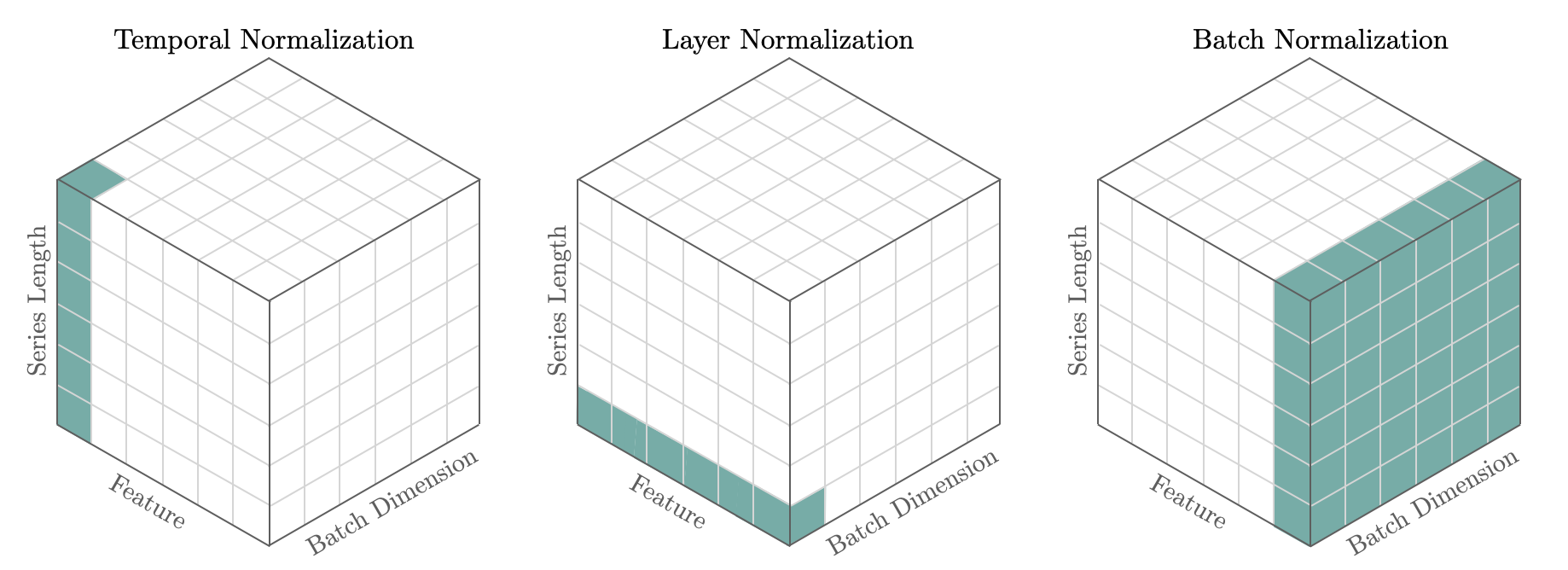
时间归一化在神经预测任务中被证明是非常重要的，因为它使网络的非线性得以充分表达。预测缩放方法特别关注时间维度，因为大多数方差存在于此，这与其他深度学习技术不同，例如 BatchNorm 在批次和时间维度上进行归一化，以及 LayerNorm 在特征维度上进行归一化。目前我们支持以下技术：std、median、norm、norm1、invariant、revin。

参考文献

• Kin G. Olivares, David Luo, Cristian Challu, Stefania La Vattiata, Max Mergenthaler, Artur Dubrawski (2023). “HINT: 分层混合网络用于一致性概率预测”. 神经信息处理系统，已提交。工作论文版本可在arxiv上获得。
• Taesung Kim 和 Jinhee Kim 和 Yunwon Tae 和 Cheonbok Park 和 Jang-Ho Choi 和 Jaegul Choo. “可逆实例归一化用于应对分布变化的准确时间序列预测”. ICLR 2022.
• David Salinas, Valentin Flunkert, Jan Gasthaus, Tim Januschowski (2020). “DeepAR: 使用自回归递归网络进行概率预测”. 国际预测期刊.

图 1. 时间归一化（左）、层归一化（中）和批归一化（右）的示意图。绿色条目显示了用于计算归一化统计量的组成部分。

import torch
import torch.nn as nn

from nbdev.showdoc import show_doc
import matplotlib.pyplot as plt

plt.rcParams["axes.grid"]=True
plt.rcParams['font.family'] = 'serif'
plt.rcParams["figure.figsize"] = (4,2)

1. 辅助函数

def masked_median(x, mask, dim=-1, keepdim=True):
    """ Masked Median

    Compute the median of tensor `x` along dim, ignoring values where 
    `mask` is False. `x` and `mask` need to be broadcastable.

    **Parameters:**<br>
    `x`: torch.Tensor to compute median of along `dim` dimension.<br>
    `mask`: torch Tensor bool with same shape as `x`, where `x` is valid and False
            where `x` should be masked. Mask should not be all False in any column of
            dimension dim to avoid NaNs from zero division.<br>
    `dim` (int, optional): Dimension to take median of. Defaults to -1.<br>
    `keepdim` (bool, optional): Keep dimension of `x` or not. Defaults to True.<br>

    **Returns:**<br>
    `x_median`: torch.Tensor with normalized values.
    """
    x_nan = x.masked_fill(mask<1, float("nan"))
    x_median, _ = x_nan.nanmedian(dim=dim, keepdim=keepdim)
    x_median = torch.nan_to_num(x_median, nan=0.0)
    return x_median

def masked_mean(x, mask, dim=-1, keepdim=True):
    """ Masked  Mean

    Compute the mean of tensor `x` along dimension, ignoring values where 
    `mask` is False. `x` and `mask` need to be broadcastable.

    **Parameters:**<br>
    `x`: torch.Tensor to compute mean of along `dim` dimension.<br>
    `mask`: torch Tensor bool with same shape as `x`, where `x` is valid and False
            where `x` should be masked. Mask should not be all False in any column of
            dimension dim to avoid NaNs from zero division.<br>
    `dim` (int, optional): Dimension to take mean of. Defaults to -1.<br>
    `keepdim` (bool, optional): Keep dimension of `x` or not. Defaults to True.<br>

    **Returns:**<br>
    `x_mean`: torch.Tensor with normalized values.
    """
    x_nan = x.masked_fill(mask<1, float("nan"))
    x_mean = x_nan.nanmean(dim=dim, keepdim=keepdim)
    x_mean = torch.nan_to_num(x_mean, nan=0.0)
    return x_mean

show_doc(masked_median, title_level=3)

show_doc(masked_mean, title_level=3)

2. 标量器

def minmax_statistics(x, mask, eps=1e-6, dim=-1):
    """ MinMax Scaler

    Standardizes temporal features by ensuring its range dweels between
    [0,1] range. This transformation is often used as an alternative 
    to the standard scaler. The scaled features are obtained as:

    $$
    \mathbf{z} = (\mathbf{x}_{[B,T,C]}-\mathrm{min}({\mathbf{x}})_{[B,1,C]})/
        (\mathrm{max}({\mathbf{x}})_{[B,1,C]}- \mathrm{min}({\mathbf{x}})_{[B,1,C]})
    $$

    **Parameters:**<br>
    `x`: torch.Tensor input tensor.<br>
    `mask`: torch Tensor bool, same dimension as `x`, indicates where `x` is valid and False
            where `x` should be masked. Mask should not be all False in any column of
            dimension dim to avoid NaNs from zero division.<br>
    `eps` (float, optional): Small value to avoid division by zero. Defaults to 1e-6.<br>
    `dim` (int, optional): Dimension over to compute min and max. Defaults to -1.<br>

    **Returns:**<br>
    `z`: torch.Tensor same shape as `x`, except scaled.
    """
    mask = mask.clone()
    mask[mask==0] = torch.inf
    mask[mask==1] = 0
    x_max = torch.max(torch.nan_to_num(x-mask,nan=-torch.inf), dim=dim, keepdim=True)[0]
    x_min = torch.min(torch.nan_to_num(x+mask,nan=torch.inf), dim=dim, keepdim=True)[0]
    x_max = x_max.type(x.dtype)
    x_min = x_min.type(x.dtype)

    # x_range 并防止除以零
    x_range = x_max - x_min
    x_range[x_range==0] = 1.0
    x_range = x_range + eps
    return x_min, x_range

def minmax_scaler(x, x_min, x_range):
    return (x - x_min) / x_range

def inv_minmax_scaler(z, x_min, x_range):
    return z * x_range + x_min

show_doc(minmax_statistics, title_level=3)

def minmax1_statistics(x, mask, eps=1e-6, dim=-1):
    """ MinMax1 Scaler

    Standardizes temporal features by ensuring its range dweels between
    [-1,1] range. This transformation is often used as an alternative 
    to the standard scaler or classic Min Max Scaler. 
    The scaled features are obtained as:

    $$\mathbf{z} = 2 (\mathbf{x}_{[B,T,C]}-\mathrm{min}({\mathbf{x}})_{[B,1,C]})/ (\mathrm{max}({\mathbf{x}})_{[B,1,C]}- \mathrm{min}({\mathbf{x}})_{[B,1,C]})-1$$

    **Parameters:**<br>
    `x`: torch.Tensor input tensor.<br>
    `mask`: torch Tensor bool, same dimension as `x`, indicates where `x` is valid and False
            where `x` should be masked. Mask should not be all False in any column of
            dimension dim to avoid NaNs from zero division.<br>
    `eps` (float, optional): Small value to avoid division by zero. Defaults to 1e-6.<br>
    `dim` (int, optional): Dimension over to compute min and max. Defaults to -1.<br>

    **Returns:**<br>
    `z`: torch.Tensor same shape as `x`, except scaled.
    """
    # 掩码值（设置为 -inf 或 +inf）
    mask = mask.clone()
    mask[mask==0] = torch.inf
    mask[mask==1] = 0
    x_max = torch.max(torch.nan_to_num(x-mask,nan=-torch.inf), dim=dim, keepdim=True)[0]
    x_min = torch.min(torch.nan_to_num(x+mask,nan=torch.inf), dim=dim, keepdim=True)[0]
    x_max = x_max.type(x.dtype)
    x_min = x_min.type(x.dtype)
    
    # x_range 并防止除以零
    x_range = x_max - x_min
    x_range[x_range==0] = 1.0
    x_range = x_range + eps
    return x_min, x_range

def minmax1_scaler(x, x_min, x_range):
    x = (x - x_min) / x_range
    z = x * (2) - 1
    return z

def inv_minmax1_scaler(z, x_min, x_range):
    z = (z + 1) / 2
    return z * x_range + x_min

show_doc(minmax1_statistics, title_level=3)

def std_statistics(x, mask, dim=-1, eps=1e-6):
    """ Standard Scaler

    Standardizes features by removing the mean and scaling
    to unit variance along the `dim` dimension. 

    For example, for `base_windows` models, the scaled features are obtained as (with dim=1):

    $$\mathbf{z} = (\mathbf{x}_{[B,T,C]}-\\bar{\mathbf{x}}_{[B,1,C]})/\hat{\sigma}_{[B,1,C]}$$

    **Parameters:**<br>
    `x`: torch.Tensor.<br>
    `mask`: torch Tensor bool, same dimension as `x`, indicates where `x` is valid and False
            where `x` should be masked. Mask should not be all False in any column of
            dimension dim to avoid NaNs from zero division.<br>
    `eps` (float, optional): Small value to avoid division by zero. Defaults to 1e-6.<br>
    `dim` (int, optional): Dimension over to compute mean and std. Defaults to -1.<br>

    **Returns:**<br>
    `z`: torch.Tensor same shape as `x`, except scaled.
    """
    x_means = masked_mean(x=x, mask=mask, dim=dim)
    x_stds = torch.sqrt(masked_mean(x=(x-x_means)**2, mask=mask, dim=dim))

    # 防止除以零
    x_stds[x_stds==0] = 1.0
    x_stds = x_stds + eps
    return x_means, x_stds

def std_scaler(x, x_means, x_stds):
    return (x - x_means) / x_stds

def inv_std_scaler(z, x_mean, x_std):
    return (z * x_std) + x_mean

show_doc(std_statistics, title_level=3)

def robust_statistics(x, mask, dim=-1, eps=1e-6):
    """ Robust Median Scaler

    Standardizes features by removing the median and scaling
    with the mean absolute deviation (mad) a robust estimator of variance.
    This scaler is particularly useful with noisy data where outliers can 
    heavily influence the sample mean / variance in a negative way.
    In these scenarios the median and amd give better results.
    
    For example, for `base_windows` models, the scaled features are obtained as (with dim=1):

    $$\mathbf{z} = (\mathbf{x}_{[B,T,C]}-\\textrm{median}(\mathbf{x})_{[B,1,C]})/\\textrm{mad}(\mathbf{x})_{[B,1,C]}$$
        
    $$\\textrm{mad}(\mathbf{x}) = \\frac{1}{N} \sum_{}|\mathbf{x} - \mathrm{median}(x)|$$

    **Parameters:**<br>
    `x`: torch.Tensor input tensor.<br>
    `mask`: torch Tensor bool, same dimension as `x`, indicates where `x` is valid and False
            where `x` should be masked. Mask should not be all False in any column of
            dimension dim to avoid NaNs from zero division.<br>
    `eps` (float, optional): Small value to avoid division by zero. Defaults to 1e-6.<br>
    `dim` (int, optional): Dimension over to compute median and mad. Defaults to -1.<br>

    **Returns:**<br>
    `z`: torch.Tensor same shape as `x`, except scaled.
    """
    x_median = masked_median(x=x, mask=mask, dim=dim)
    x_mad = masked_median(x=torch.abs(x-x_median), mask=mask, dim=dim)

    # 保护x_mad=0的值
    # 假设正态分布且mad与std之间存在关系
    x_means = masked_mean(x=x, mask=mask, dim=dim)
    x_stds = torch.sqrt(masked_mean(x=(x-x_means)**2, mask=mask, dim=dim))  
    x_mad_aux = x_stds * 0.6744897501960817
    x_mad = x_mad * (x_mad>0) + x_mad_aux * (x_mad==0)
    
    # 防止除以零
    x_mad[x_mad==0] = 1.0
    x_mad = x_mad + eps
    return x_median, x_mad

def robust_scaler(x, x_median, x_mad):
    return (x - x_median) / x_mad

def inv_robust_scaler(z, x_median, x_mad):
    return z * x_mad + x_median

show_doc(robust_statistics, title_level=3)

def invariant_statistics(x, mask, dim=-1, eps=1e-6):
    """ Invariant Median Scaler

    Standardizes features by removing the median and scaling
    with the mean absolute deviation (mad) a robust estimator of variance.
    Aditionally it complements the transformation with the arcsinh transformation.

    For example, for `base_windows` models, the scaled features are obtained as (with dim=1):

    $$\mathbf{z} = (\mathbf{x}_{[B,T,C]}-\\textrm{median}(\mathbf{x})_{[B,1,C]})/\\textrm{mad}(\mathbf{x})_{[B,1,C]}$$

    $$\mathbf{z} = \\textrm{arcsinh}(\mathbf{z})$$

    **Parameters:**<br>
    `x`: torch.Tensor input tensor.<br>
    `mask`: torch Tensor bool, same dimension as `x`, indicates where `x` is valid and False
            where `x` should be masked. Mask should not be all False in any column of
            dimension dim to avoid NaNs from zero division.<br>
    `eps` (float, optional): Small value to avoid division by zero. Defaults to 1e-6.<br>
    `dim` (int, optional): Dimension over to compute median and mad. Defaults to -1.<br>

    **Returns:**<br>
    `z`: torch.Tensor same shape as `x`, except scaled.
    """
    x_median = masked_median(x=x, mask=mask, dim=dim)
    x_mad = masked_median(x=torch.abs(x-x_median), mask=mask, dim=dim)

    # 保护x_mad=0的值
    # 假设正态分布且mad与std之间存在关系
    x_means = masked_mean(x=x, mask=mask, dim=dim)
    x_stds = torch.sqrt(masked_mean(x=(x-x_means)**2, mask=mask, dim=dim))        
    x_mad_aux = x_stds * 0.6744897501960817
    x_mad = x_mad * (x_mad>0) + x_mad_aux * (x_mad==0)

    # 防止除以零
    x_mad[x_mad==0] = 1.0
    x_mad = x_mad + eps
    return x_median, x_mad

def invariant_scaler(x, x_median, x_mad):
    return torch.arcsinh((x - x_median) / x_mad)

def inv_invariant_scaler(z, x_median, x_mad):
    return torch.sinh(z) * x_mad + x_median

show_doc(invariant_statistics, title_level=3)

def identity_statistics(x, mask, dim=-1, eps=1e-6):
    """ Identity Scaler

    A placeholder identity scaler, that is argument insensitive.

    **Parameters:**<br>
    `x`: torch.Tensor input tensor.<br>
    `mask`: torch Tensor bool, same dimension as `x`, indicates where `x` is valid and False
            where `x` should be masked. Mask should not be all False in any column of
            dimension dim to avoid NaNs from zero division.<br>
    `eps` (float, optional): Small value to avoid division by zero. Defaults to 1e-6.<br>
    `dim` (int, optional): Dimension over to compute median and mad. Defaults to -1.<br>

    **Returns:**<br>
    `x`: original torch.Tensor `x`.
    """
    # 折叠维度
    shape = list(x.shape)
    shape[dim] = 1

    x_shift = torch.zeros(shape, device=x.device)
    x_scale = torch.ones(shape, device=x.device)

    return x_shift, x_scale

def identity_scaler(x, x_shift, x_scale):
    return x

def inv_identity_scaler(z, x_shift, x_scale):
    return z

show_doc(identity_statistics, title_level=3)

3. 时间归一化模块

class TemporalNorm(nn.Module):
    """ Temporal Normalization

    Standardization of the features is a common requirement for many 
    machine learning estimators, and it is commonly achieved by removing 
    the level and scaling its variance. The `TemporalNorm` module applies 
    temporal normalization over the batch of inputs as defined by the type of scaler.

    $$\mathbf{z}_{[B,T,C]} = \\textrm{Scaler}(\mathbf{x}_{[B,T,C]})$$

    If `scaler_type` is `revin` learnable normalization parameters are added on top of
    the usual normalization technique, the parameters are learned through scale decouple
    global skip connections. The technique is available for point and probabilistic outputs.

    $$\mathbf{\hat{z}}_{[B,T,C]} = \\boldsymbol{\hat{\\gamma}}_{[1,1,C]} \mathbf{z}_{[B,T,C]} +\\boldsymbol{\hat{\\beta}}_{[1,1,C]}$$

    **Parameters:**<br>
    `scaler_type`: str, defines the type of scaler used by TemporalNorm. Available [`identity`, `standard`, `robust`, `minmax`, `minmax1`, `invariant`, `revin`].<br>
    `dim` (int, optional): Dimension over to compute scale and shift. Defaults to -1.<br>
    `eps` (float, optional): Small value to avoid division by zero. Defaults to 1e-6.<br>
    `num_features`: int=None, for RevIN-like learnable affine parameters initialization.<br>

    **References**<br>
    - [Kin G. Olivares, David Luo, Cristian Challu, Stefania La Vattiata, Max Mergenthaler, Artur Dubrawski (2023). "HINT: Hierarchical Mixture Networks For Coherent Probabilistic Forecasting". Neural Information Processing Systems, submitted. Working Paper version available at arxiv.](https://arxiv.org/abs/2305.07089)<br>
    """
    def __init__(self, scaler_type='robust', dim=-1, eps=1e-6, num_features=None):
        super().__init__()
        compute_statistics = {None: identity_statistics,
                              'identity': identity_statistics,
                              'standard': std_statistics,
                              'revin': std_statistics,
                              'robust': robust_statistics,
                              'minmax': minmax_statistics,
                              'minmax1': minmax1_statistics,
                              'invariant': invariant_statistics,}
        scalers = {None: identity_scaler,
                   'identity': identity_scaler,
                   'standard': std_scaler,
                   'revin': std_scaler,
                   'robust': robust_scaler,
                   'minmax': minmax_scaler,
                   'minmax1': minmax1_scaler,
                   'invariant':invariant_scaler,}
        inverse_scalers = {None: inv_identity_scaler,
                    'identity': inv_identity_scaler,
                    'standard': inv_std_scaler,
                    'revin': inv_std_scaler,
                    'robust': inv_robust_scaler,
                    'minmax': inv_minmax_scaler,
                    'minmax1': inv_minmax1_scaler,
                    'invariant': inv_invariant_scaler,}
        assert (scaler_type in scalers.keys()), f'{scaler_type} not defined'
        if (scaler_type=='revin') and (num_features is None):
            raise Exception('You must pass num_features for ReVIN scaler.')

        self.compute_statistics = compute_statistics[scaler_type]
        self.scaler = scalers[scaler_type]
        self.inverse_scaler = inverse_scalers[scaler_type]
        self.scaler_type = scaler_type
        self.dim = dim
        self.eps = eps

        if (scaler_type=='revin'):
            self._init_params(num_features=num_features)

    def _init_params(self, num_features):
        # 初始化RevIN缩放器参数以进行广播：
        if self.dim==1: # [B,T,C]  [1,1,C]
            self.revin_bias = nn.Parameter(torch.zeros(1,1,num_features))
            self.revin_weight = nn.Parameter(torch.ones(1,1,num_features))
        elif self.dim==-1: # [B,C,T]  [1,C,1]
            self.revin_bias = nn.Parameter(torch.zeros(1,num_features,1))
            self.revin_weight = nn.Parameter(torch.ones(1,num_features,1))

    #@torch.no_grad()
    def transform(self, x, mask):
        """ Center and scale the data.

        **Parameters:**<br>
        `x`: torch.Tensor shape [batch, time, channels].<br>
        `mask`: torch Tensor bool, shape  [batch, time] where `x` is valid and False
                where `x` should be masked. Mask should not be all False in any column of
                dimension dim to avoid NaNs from zero division.<br>

        **Returns:**<br>
        `z`: torch.Tensor same shape as `x`, except scaled.
        """
        x_shift, x_scale = self.compute_statistics(x=x, mask=mask, dim=self.dim, eps=self.eps)
        self.x_shift = x_shift
        self.x_scale = x_scale

        # 原版Revin执行此操作
        # z = self.revin_weight * z
        # z = z + 自.revin_bias
        # 然而，这仅适用于点预测，不适用于
        # distribution's scale decouple technique.
        if self.scaler_type=='revin':
            self.x_shift = self.x_shift + self.revin_bias
            self.x_scale = self.x_scale * (torch.relu(self.revin_weight) + self.eps)

        z = self.scaler(x, x_shift, x_scale)
        return z

    #@torch.no_grad()
    def inverse_transform(self, z, x_shift=None, x_scale=None):
        """ Scale back the data to the original representation.

        **Parameters:**<br>
        `z`: torch.Tensor shape [batch, time, channels], scaled.<br>

        **Returns:**<br>
        `x`: torch.Tensor original data.
        """

        if x_shift is None:
            x_shift = self.x_shift
        if x_scale is None:
            x_scale = self.x_scale

        # 原版Revin执行此操作
        # z = z - self.revin_bias
        # z = (z / (self.revin_weight + self.eps))
        # 然而，这仅适用于点预测，不适用于
        # distribution's scale decouple technique.

        x = self.inverse_scaler(z, x_shift, x_scale)
        return x

    def forward(self, x):
        # 梯度是从BaseWindows/BaseRecurrent前向传播中获得的。
        pass

show_doc(TemporalNorm, name='TemporalNorm', title_level=3)

show_doc(TemporalNorm.transform, title_level=3)

show_doc(TemporalNorm.inverse_transform, title_level=3)

示例

import numpy as np

# 声明合成批次以标准化
x1 = 10**0 * np.arange(36)[:, None]
x2 = 10**1 * np.arange(36)[:, None]

np_x = np.concatenate([x1, x2], axis=1)
np_x = np.repeat(np_x[None, :,:], repeats=2, axis=0)
np_x[0,:,:] = np_x[0,:,:] + 100

np_mask = np.ones(np_x.shape)
np_mask[:, -12:, :] = 0

print(f'x.shape [batch, time, features]={np_x.shape}')
print(f'mask.shape [batch, time, features]={np_mask.shape}')

# 验证标量
x = 1.0*torch.tensor(np_x)
mask = torch.tensor(np_mask)
scaler = TemporalNorm(scaler_type='standard', dim=1)
x_scaled = scaler.transform(x=x, mask=mask)
x_recovered = scaler.inverse_transform(x_scaled)

plt.plot(x[0,:,0], label='x1', color='#78ACA8')
plt.plot(x[0,:,1], label='x2',  color='#E3A39A')
plt.title('Before TemporalNorm')
plt.xlabel('Time')
plt.legend()
plt.show()

plt.plot(x_scaled[0,:,0], label='x1', color='#78ACA8')
plt.plot(x_scaled[0,:,1]+0.1, label='x2+0.1', color='#E3A39A')
plt.title(f'TemporalNorm \'{scaler.scaler_type}\' ')
plt.xlabel('Time')
plt.legend()
plt.show()

plt.plot(x_recovered[0,:,0], label='x1', color='#78ACA8')
plt.plot(x_recovered[0,:,1], label='x2', color='#E3A39A')
plt.title('Recovered')
plt.xlabel('Time')
plt.legend()
plt.show()

# 验证标量
for scaler_type in [None, 'identity', 'standard', 'robust', 'minmax', 'minmax1', 'invariant', 'revin']:
    x = 1.0*torch.tensor(np_x)
    mask = torch.tensor(np_mask)
    scaler = TemporalNorm(scaler_type=scaler_type, dim=1, num_features=np_x.shape[-1])
    x_scaled = scaler.transform(x=x, mask=mask)
    x_recovered = scaler.inverse_transform(x_scaled)
    assert torch.allclose(x, x_recovered, atol=1e-3), f'Recovered data is not the same as original with {scaler_type}'

import pandas as pd

from neuralforecast import NeuralForecast
from neuralforecast.models import NHITS
from neuralforecast.utils import AirPassengersDF as Y_df

# 掩码预测过滤的单元测试
model = NHITS(h=12,
              input_size=12*2,
              max_steps=1,
              windows_batch_size=None, 
              n_freq_downsample=[1,1,1],
              scaler_type='minmax')

nf = NeuralForecast(models=[model], freq='M')
nf.fit(df=Y_df)
Y_hat = nf.predict(df=Y_df)
assert pd.isnull(Y_hat).sum().sum() == 0, 'Predictions should not have NaNs'

from neuralforecast import NeuralForecast
from neuralforecast.models import NHITS, RNN
from neuralforecast.losses.pytorch import DistributionLoss, HuberLoss, GMM, MAE
from neuralforecast.tsdataset import TimeSeriesDataset
from neuralforecast.utils import AirPassengers, AirPassengersPanel, AirPassengersStatic

# Unit test for ReVIN, and its compatibility with distribution's scale decouple
Y_df = AirPassengersPanel
# del Y_df['trend']

# Instantiate BaseWindow model and test revin dynamic dimensionality with hist_exog_list
model = NHITS(h=12,
              input_size=24,
              loss=GMM(n_components=10, level=[90]),
              hist_exog_list=['y_[lag12]'],
              max_steps=1,
              early_stop_patience_steps=10,
              val_check_steps=50,
              scaler_type='revin',
              learning_rate=1e-3)
nf = NeuralForecast(models=[model], freq='MS')
Y_hat_df = nf.cross_validation(df=Y_df, val_size=12, n_windows=1)

# Instantiate BaseWindow model and test revin dynamic dimensionality with hist_exog_list
model = NHITS(h=12,
              input_size=24,
              loss=HuberLoss(),
              hist_exog_list=['trend', 'y_[lag12]'],
              max_steps=1,
              early_stop_patience_steps=10,
              val_check_steps=50,
              scaler_type='revin',
              learning_rate=1e-3)
nf = NeuralForecast(models=[model], freq='MS')
Y_hat_df = nf.cross_validation(df=Y_df, val_size=12, n_windows=1)

# Instantiate BaseRecurrent model and test revin dynamic dimensionality with hist_exog_list
model = RNN(h=12,
              input_size=24,
              loss=GMM(n_components=10, level=[90]),
              hist_exog_list=['trend', 'y_[lag12]'],
              max_steps=1,
              early_stop_patience_steps=10,
              val_check_steps=50,
              scaler_type='revin',
              learning_rate=1e-3)
nf = NeuralForecast(models=[model], freq='MS')
Y_hat_df = nf.cross_validation(df=Y_df, val_size=12, n_windows=1)

# Instantiate BaseRecurrent model and test revin dynamic dimensionality with hist_exog_list
model = RNN(h=12,
              input_size=24,
              loss=HuberLoss(),
              hist_exog_list=['trend'],
              max_steps=1,
              early_stop_patience_steps=10,
              val_check_steps=50,
              scaler_type='revin',
              learning_rate=1e-3)
nf = NeuralForecast(models=[model], freq='MS')
Y_hat_df = nf.cross_validation(df=Y_df, val_size=12, n_windows=1)

Give us a ⭐ on Github