NumPy 评估

%load_ext autoreload
%autoreload 2

NeuralForecast 包含一组旨在模型评估过程中使用的 NumPy 损失函数。

最重要的训练信号是预测误差，它是观察值 \(y_{\tau}\) 和预测值 \(\hat{y}_{\tau}\) 之间的差异，在时间 \(y_{\tau}\)：

\[e_{\tau} = y_{\tau}-\hat{y}_{\tau} \qquad \qquad \tau \in \{t+1,\dots,t+H \}\]

训练损失总结了不同评估指标下的预测误差。

from typing import Optional, Union

import numpy as np

from IPython.display import Image
from nbdev.showdoc import show_doc

WIDTH = 600
HEIGHT = 300

def _divide_no_nan(a: np.ndarray, b: np.ndarray) -> np.ndarray:
    """
    处理除以零的辅助功能
    """
    div = a / b
    div[div != div] = 0.0
    div[div == float('inf')] = 0.0
    return div

def _metric_protections(y: np.ndarray, y_hat: np.ndarray, 
                        weights: Optional[np.ndarray]) -> None:
    assert (weights is None) or (np.sum(weights) > 0), 'Sum of weights cannot be 0'
    assert (weights is None) or (weights.shape == y.shape),\
        f'Wrong weight dimension weights.shape {weights.shape}, y.shape {y.shape}'

1. 规模依赖错误

这些指标与数据处于相同的尺度上。

平均绝对误差

def mae(y: np.ndarray, y_hat: np.ndarray,
        weights: Optional[np.ndarray] = None,
        axis: Optional[int] = None) -> Union[float, np.ndarray]:
    """Mean Absolute Error

    Calculates Mean Absolute Error between
    `y` and `y_hat`. MAE measures the relative prediction
    accuracy of a forecasting method by calculating the
    deviation of the prediction and the true
    value at a given time and averages these devations
    over the length of the series.

    $$ \mathrm{MAE}(\\mathbf{y}_{\\tau}, \\mathbf{\hat{y}}_{\\tau}) = \\frac{1}{H} \\sum^{t+H}_{\\tau=t+1} |y_{\\tau} - \hat{y}_{\\tau}| $$

    **Parameters:**<br>
    `y`: numpy array, Actual values.<br>
    `y_hat`: numpy array, Predicted values.<br>
    `mask`: numpy array, Specifies date stamps per serie to consider in loss.<br>

    **Returns:**<br>
    `mae`: numpy array, (single value).    
    """
    _metric_protections(y, y_hat, weights)
    
    delta_y = np.abs(y - y_hat)
    if weights is not None:
        mae = np.average(delta_y[~np.isnan(delta_y)], 
                         weights=weights[~np.isnan(delta_y)],
                         axis=axis)
    else:
        mae = np.nanmean(delta_y, axis=axis)
        
    return mae

show_doc(mae, title_level=3)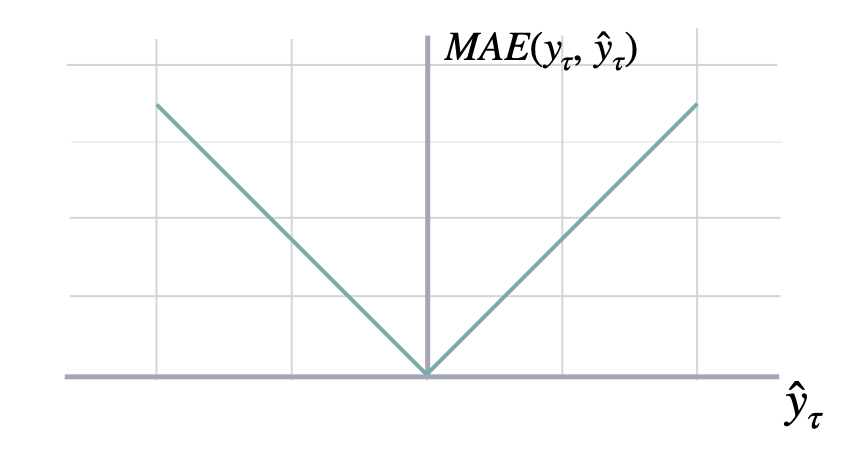

均方误差

def mse(y: np.ndarray, y_hat: np.ndarray, 
        weights: Optional[np.ndarray] = None,
        axis: Optional[int] = None) -> Union[float, np.ndarray]:
    """  Mean Squared Error

    Calculates Mean Squared Error between
    `y` and `y_hat`. MSE measures the relative prediction
    accuracy of a forecasting method by calculating the 
    squared deviation of the prediction and the true
    value at a given time, and averages these devations
    over the length of the series.

    $$ \mathrm{MSE}(\\mathbf{y}_{\\tau}, \\mathbf{\hat{y}}_{\\tau}) = \\frac{1}{H} \\sum^{t+H}_{\\tau=t+1} (y_{\\tau} - \hat{y}_{\\tau})^{2} $$

    **Parameters:**<br>
    `y`: numpy array, Actual values.<br>
    `y_hat`: numpy array, Predicted values.<br>
    `mask`: numpy array, Specifies date stamps per serie to consider in loss.<br>

    **Returns:**<br>
    `mse`: numpy array, (single value).
    """
    _metric_protections(y, y_hat, weights)

    delta_y = np.square(y - y_hat)
    if weights is not None:
        mse = np.average(delta_y[~np.isnan(delta_y)],
                         weights=weights[~np.isnan(delta_y)],
                         axis=axis)
    else:
        mse = np.nanmean(delta_y, axis=axis)

    return mse

show_doc(mse, title_level=3)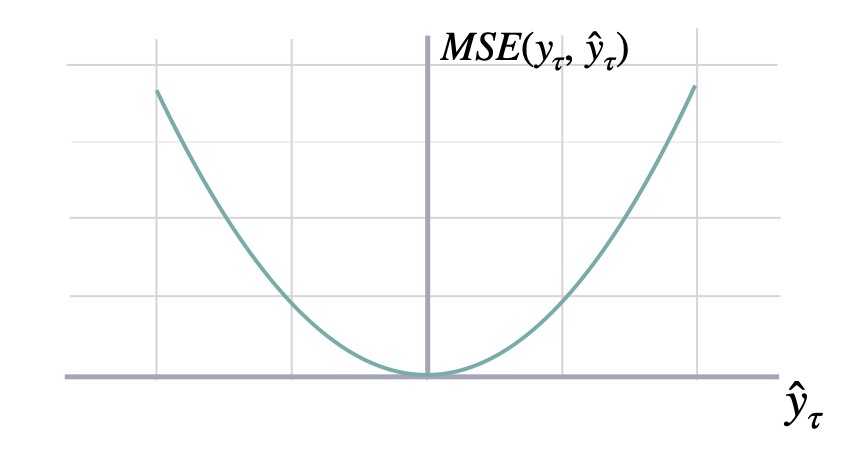

均方根误差

def rmse(y: np.ndarray, y_hat: np.ndarray,
         weights: Optional[np.ndarray] = None,
         axis: Optional[int] = None) -> Union[float, np.ndarray]:
    """ Root Mean Squared Error

    Calculates Root Mean Squared Error between
    `y` and `y_hat`. RMSE measures the relative prediction
    accuracy of a forecasting method by calculating the squared deviation
    of the prediction and the observed value at a given time and
    averages these devations over the length of the series.
    Finally the RMSE will be in the same scale
    as the original time series so its comparison with other
    series is possible only if they share a common scale.
    RMSE has a direct connection to the L2 norm.

    $$ \mathrm{RMSE}(\\mathbf{y}_{\\tau}, \\mathbf{\hat{y}}_{\\tau}) = \\sqrt{\\frac{1}{H} \\sum^{t+H}_{\\tau=t+1} (y_{\\tau} - \hat{y}_{\\tau})^{2}} $$

    **Parameters:**<br>
    `y`: numpy array, Actual values.<br>
    `y_hat`: numpy array, Predicted values.<br>
    `mask`: numpy array, Specifies date stamps per serie to consider in loss.<br>

    **Returns:**<br>
    `rmse`: numpy array, (single value).
    """
    return np.sqrt(mse(y, y_hat, weights, axis))

show_doc(rmse, title_level=3)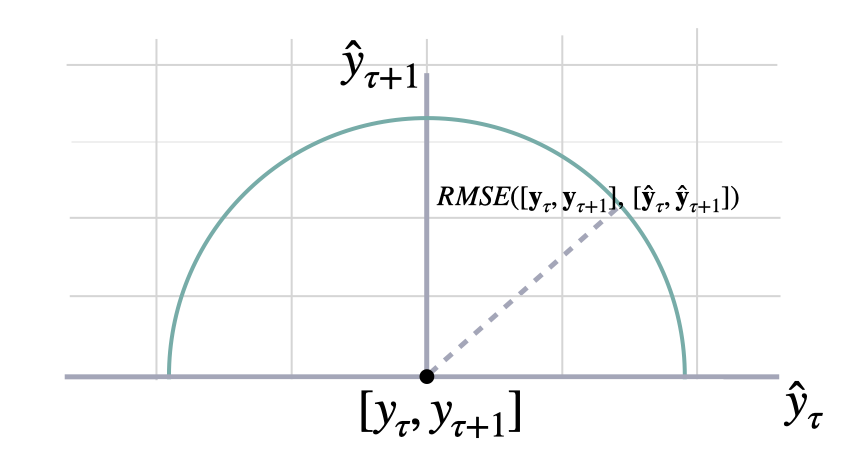

2. 百分比误差

这些指标是无单位的，适合于系列之间的比较。

平均绝对百分比误差

def mape(y: np.ndarray, y_hat: np.ndarray, 
         weights: Optional[np.ndarray] = None,
         axis: Optional[int] = None) -> Union[float, np.ndarray]:
    """ Mean Absolute Percentage Error

    Calculates Mean Absolute Percentage Error  between
    `y` and `y_hat`. MAPE measures the relative prediction
    accuracy of a forecasting method by calculating the percentual deviation
    of the prediction and the observed value at a given time and
    averages these devations over the length of the series.
    The closer to zero an observed value is, the higher penalty MAPE loss
    assigns to the corresponding error.

    $$ \mathrm{MAPE}(\\mathbf{y}_{\\tau}, \\mathbf{\hat{y}}_{\\tau}) = \\frac{1}{H} \\sum^{t+H}_{\\tau=t+1} \\frac{|y_{\\tau}-\hat{y}_{\\tau}|}{|y_{\\tau}|} $$

    **Parameters:**<br>
    `y`: numpy array, Actual values.<br>
    `y_hat`: numpy array, Predicted values.<br>
    `mask`: numpy array, Specifies date stamps per serie to consider in loss.<br>

    **Returns:**<br>
    `mape`: numpy array, (single value).
    """
    _metric_protections(y, y_hat, weights)
        
    delta_y = np.abs(y - y_hat)
    scale = np.abs(y)
    mape = _divide_no_nan(delta_y, scale)
    mape = np.average(mape, weights=weights, axis=axis)
    
    return mape

show_doc(mape, title_level=3)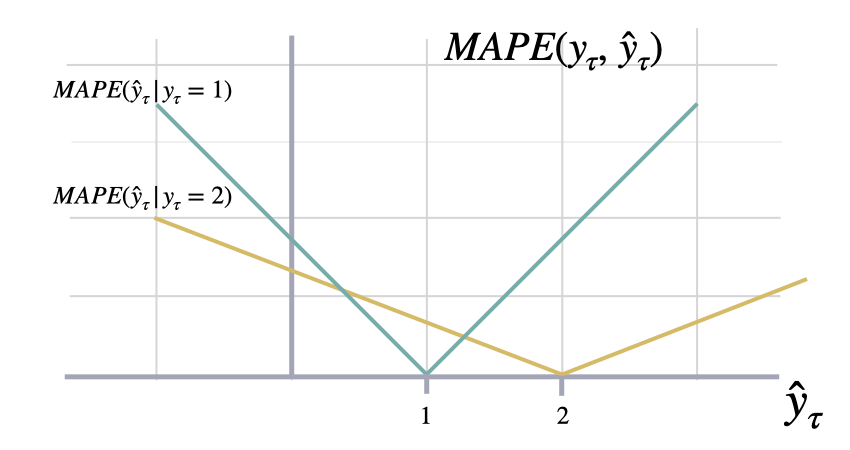

SMAPE

SMAPE（对称平均绝对百分比误差）是一种衡量预测值与实际值之间差异的指标。它的计算公式如下：

[ SMAPE = _{t=1}^{n} ]

其中： - (F_t) 是预测值 - (A_t) 是实际值 - (n) 是样本总数

SMAPE 的值范围从 0% 到 200%，值越小表示模型的预测性能越好。

def smape(y: np.ndarray, y_hat: np.ndarray,
          weights: Optional[np.ndarray] = None,
          axis: Optional[int] = None) -> Union[float, np.ndarray]:
    """ Symmetric Mean Absolute Percentage Error

    Calculates Symmetric Mean Absolute Percentage Error between
    `y` and `y_hat`. SMAPE measures the relative prediction
    accuracy of a forecasting method by calculating the relative deviation
    of the prediction and the observed value scaled by the sum of the
    absolute values for the prediction and observed value at a
    given time, then averages these devations over the length
    of the series. This allows the SMAPE to have bounds between
    0% and 200% which is desirable compared to normal MAPE that
    may be undetermined when the target is zero.

    $$ \mathrm{sMAPE}_{2}(\\mathbf{y}_{\\tau}, \\mathbf{\hat{y}}_{\\tau}) = \\frac{1}{H} \\sum^{t+H}_{\\tau=t+1} \\frac{|y_{\\tau}-\hat{y}_{\\tau}|}{|y_{\\tau}|+|\hat{y}_{\\tau}|} $$

    **Parameters:**<br>
    `y`: numpy array, Actual values.<br>
    `y_hat`: numpy array, Predicted values.<br>
    `mask`: numpy array, Specifies date stamps per serie to consider in loss.<br>

    **Returns:**<br>
    `smape`: numpy array, (single value).
    
    **References:**<br>
    [Makridakis S., "Accuracy measures: theoretical and practical concerns".](https://www.sciencedirect.com/science/article/pii/0169207093900793)
    """
    _metric_protections(y, y_hat, weights)
        
    delta_y = np.abs(y - y_hat)
    scale = np.abs(y) + np.abs(y_hat)
    smape = _divide_no_nan(delta_y, scale)
    smape = 2 * np.average(smape, weights=weights, axis=axis)
    
    if isinstance(smape, float):
        assert smape <= 2, 'SMAPE should be lower than 200'
    else:
        assert all(smape <= 2), 'SMAPE should be lower than 200'
    
    return smape

show_doc(smape, title_level=3)

3. 与规模无关的误差

这些指标测量相对于基线的相对改进。

平均绝对尺度误差

def mase(y: np.ndarray, y_hat: np.ndarray, 
         y_train: np.ndarray,
         seasonality: int,
         weights: Optional[np.ndarray] = None,
         axis: Optional[int] = None) -> Union[float, np.ndarray]:
    """ Mean Absolute Scaled Error 
    Calculates the Mean Absolute Scaled Error between
    `y` and `y_hat`. MASE measures the relative prediction
    accuracy of a forecasting method by comparinng the mean absolute errors
    of the prediction and the observed value against the mean
    absolute errors of the seasonal naive model.
    The MASE partially composed the Overall Weighted Average (OWA), 
    used in the M4 Competition.

    $$ \mathrm{MASE}(\\mathbf{y}_{\\tau}, \\mathbf{\hat{y}}_{\\tau}, \\mathbf{\hat{y}}^{season}_{\\tau}) = \\frac{1}{H} \sum^{t+H}_{\\tau=t+1} \\frac{|y_{\\tau}-\hat{y}_{\\tau}|}{\mathrm{MAE}(\\mathbf{y}_{\\tau}, \\mathbf{\hat{y}}^{season}_{\\tau})} $$

    **Parameters:**<br>
    `y`: numpy array, (batch_size, output_size), Actual values.<br>
    `y_hat`: numpy array, (batch_size, output_size)), Predicted values.<br>
    `y_insample`: numpy array, (batch_size, input_size), Actual insample Seasonal Naive predictions.<br>
    `seasonality`: int. Main frequency of the time series; Hourly 24,  Daily 7, Weekly 52, Monthly 12, Quarterly 4, Yearly 1.        
    `mask`: numpy array, Specifies date stamps per serie to consider in loss.<br>

    **Returns:**<br>
    `mase`: numpy array, (single value).
    
    **References:**<br>
    [Rob J. Hyndman, & Koehler, A. B. "Another look at measures of forecast accuracy".](https://www.sciencedirect.com/science/article/pii/S0169207006000239)<br>
    [Spyros Makridakis, Evangelos Spiliotis, Vassilios Assimakopoulos, "The M4 Competition: 100,000 time series and 61 forecasting methods".](https://www.sciencedirect.com/science/article/pii/S0169207019301128)
    """
    delta_y = np.abs(y - y_hat)
    delta_y = np.average(delta_y, weights=weights, axis=axis)

    scale = np.abs(y_train[:-seasonality] - y_train[seasonality:])
    scale = np.average(scale, axis=axis)

    mase = delta_y / scale

    return mase

show_doc(mase, title_level=3)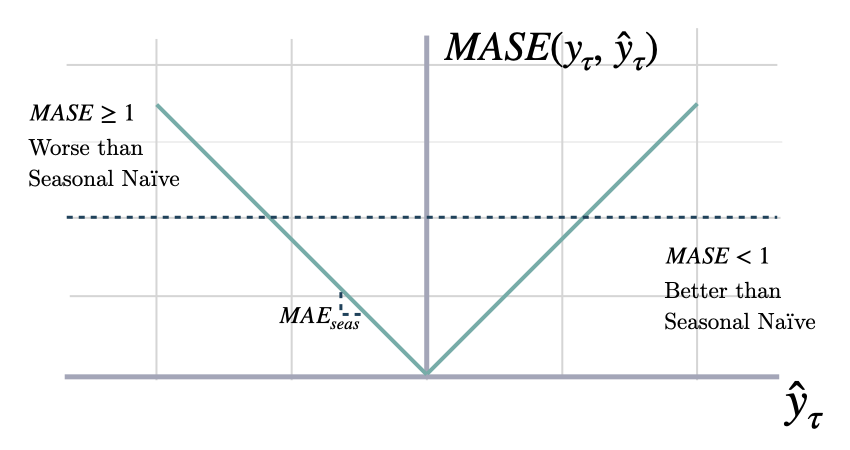

相对平均绝对误差

def rmae(y: np.ndarray, 
         y_hat1: np.ndarray, y_hat2: np.ndarray, 
         weights: Optional[np.ndarray] = None,
         axis: Optional[int] = None) -> Union[float, np.ndarray]:
    """ RMAE
            
    Calculates Relative Mean Absolute Error (RMAE) between
    two sets of forecasts (from two different forecasting methods).
    A number smaller than one implies that the forecast in the 
    numerator is better than the forecast in the denominator.
    
    $$ \mathrm{rMAE}(\\mathbf{y}_{\\tau}, \\mathbf{\hat{y}}_{\\tau}, \\mathbf{\hat{y}}^{base}_{\\tau}) = \\frac{1}{H} \sum^{t+H}_{\\tau=t+1} \\frac{|y_{\\tau}-\hat{y}_{\\tau}|}{\mathrm{MAE}(\\mathbf{y}_{\\tau}, \\mathbf{\hat{y}}^{base}_{\\tau})} $$
    
    **Parameters:**<br>
    `y`: numpy array, observed values.<br>
    `y_hat1`: numpy array. Predicted values of first model.<br>
    `y_hat2`: numpy array. Predicted values of baseline model.<br>
    `weights`: numpy array, optional. Weights for weighted average.<br>
    `axis`: None or int, optional.Axis or axes along which to average a.<br> 
        The default, axis=None, will average over all of the elements of
        the input array.
    
    **Returns:**<br>
    `rmae`: numpy array or double.

    **References:**<br>
    [Rob J. Hyndman, & Koehler, A. B. "Another look at measures of forecast accuracy".](https://www.sciencedirect.com/science/article/pii/S0169207006000239)
    """
    numerator = mae(y=y, y_hat=y_hat1, weights=weights, axis=axis)
    denominator = mae(y=y, y_hat=y_hat2, weights=weights, axis=axis)
    rmae = numerator / denominator

    return rmae

show_doc(rmae, title_level=3)

4. 概率误差

这些测量绝对偏差不对称，导致低估/高估。

分位数损失

def quantile_loss(y: np.ndarray, y_hat: np.ndarray, q: float = 0.5, 
                  weights: Optional[np.ndarray] = None,
                  axis: Optional[int] = None) -> Union[float, np.ndarray]:
    """ Quantile Loss

    Computes the quantile loss between `y` and `y_hat`.
    QL measures the deviation of a quantile forecast.
    By weighting the absolute deviation in a non symmetric way, the
    loss pays more attention to under or over estimation.
    A common value for q is 0.5 for the deviation from the median (Pinball loss).

    $$ \mathrm{QL}(\\mathbf{y}_{\\tau}, \\mathbf{\hat{y}}^{(q)}_{\\tau}) = \\frac{1}{H} \\sum^{t+H}_{\\tau=t+1} \Big( (1-q)\,( \hat{y}^{(q)}_{\\tau} - y_{\\tau} )_{+} + q\,( y_{\\tau} - \hat{y}^{(q)}_{\\tau} )_{+} \Big) $$

    **Parameters:**<br>
    `y`: numpy array, Actual values.<br>
    `y_hat`: numpy array, Predicted values.<br>
    `q`: float, between 0 and 1. The slope of the quantile loss, in the context of quantile regression, the q determines the conditional quantile level.<br>
    `mask`: numpy array, Specifies date stamps per serie to consider in loss.<br>

    **Returns:**<br>
    `quantile_loss`: numpy array, (single value).
    
    **References:**<br>
    [Roger Koenker and Gilbert Bassett, Jr., "Regression Quantiles".](https://www.jstor.org/stable/1913643)
    """
    _metric_protections(y, y_hat, weights)

    delta_y = y - y_hat
    loss = np.maximum(q * delta_y, (q - 1) * delta_y)

    if weights is not None:
        quantile_loss = np.average(loss[~np.isnan(loss)], 
                             weights=weights[~np.isnan(loss)],
                             axis=axis)
    else:
        quantile_loss = np.nanmean(loss, axis=axis)
        
    return quantile_loss

show_doc(quantile_loss, title_level=3)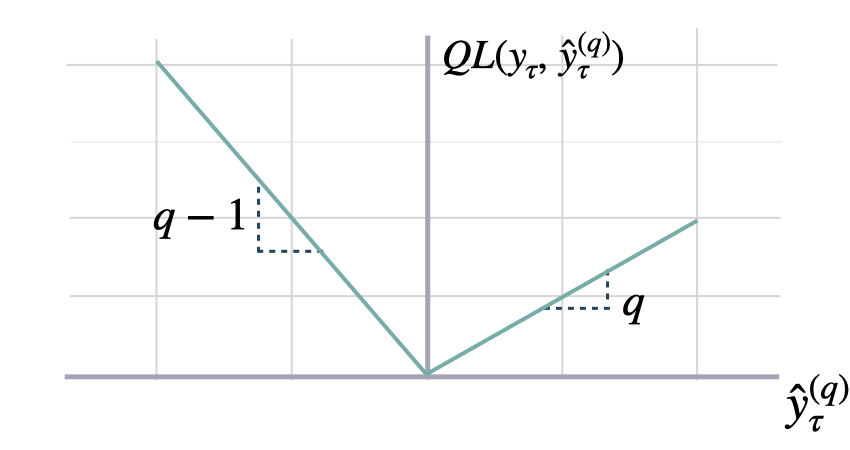

多分位数损失

def mqloss(y: np.ndarray, y_hat: np.ndarray, 
           quantiles: np.ndarray, 
           weights: Optional[np.ndarray] = None,
           axis: Optional[int] = None) -> Union[float, np.ndarray]:
    """  Multi-Quantile loss

    Calculates the Multi-Quantile loss (MQL) between `y` and `y_hat`.
    MQL calculates the average multi-quantile Loss for
    a given set of quantiles, based on the absolute 
    difference between predicted quantiles and observed values.

    $$ \mathrm{MQL}(\\mathbf{y}_{\\tau},[\\mathbf{\hat{y}}^{(q_{1})}_{\\tau}, ... ,\hat{y}^{(q_{n})}_{\\tau}]) = \\frac{1}{n} \\sum_{q_{i}} \mathrm{QL}(\\mathbf{y}_{\\tau}, \\mathbf{\hat{y}}^{(q_{i})}_{\\tau}) $$

    The limit behavior of MQL allows to measure the accuracy 
    of a full predictive distribution $\mathbf{\hat{F}}_{\\tau}$ with 
    the continuous ranked probability score (CRPS). This can be achieved 
    through a numerical integration technique, that discretizes the quantiles 
    and treats the CRPS integral with a left Riemann approximation, averaging over 
    uniformly distanced quantiles.    

    $$ \mathrm{CRPS}(y_{\\tau}, \mathbf{\hat{F}}_{\\tau}) = \int^{1}_{0} \mathrm{QL}(y_{\\tau}, \hat{y}^{(q)}_{\\tau}) dq $$

    **Parameters:**<br>
    `y`: numpy array, Actual values.<br>
    `y_hat`: numpy array, Predicted values.<br>
    `quantiles`: numpy array,(n_quantiles). Quantiles to estimate from the distribution of y.<br>
    `mask`: numpy array, Specifies date stamps per serie to consider in loss.<br>

    **Returns:**<br>
    `mqloss`: numpy array, (single value).
    
    **References:**<br>
    [Roger Koenker and Gilbert Bassett, Jr., "Regression Quantiles".](https://www.jstor.org/stable/1913643)<br>
    [James E. Matheson and Robert L. Winkler, "Scoring Rules for Continuous Probability Distributions".](https://www.jstor.org/stable/2629907)
    """
    if weights is None: weights = np.ones(y.shape)
        
    _metric_protections(y, y_hat, weights)
    n_q = len(quantiles)
    
    y_rep  = np.expand_dims(y, axis=-1)
    error  = y_hat - y_rep
    sq     = np.maximum(-error, np.zeros_like(error))
    s1_q   = np.maximum(error, np.zeros_like(error))
    mqloss = (quantiles * sq + (1 - quantiles) * s1_q)
    
    # 匹配y/权重维度并计算加权平均值
    weights = np.repeat(np.expand_dims(weights, axis=-1), repeats=n_q, axis=-1)
    mqloss  = np.average(mqloss, weights=weights, axis=axis)

    return mqloss

show_doc(mqloss, title_level=3)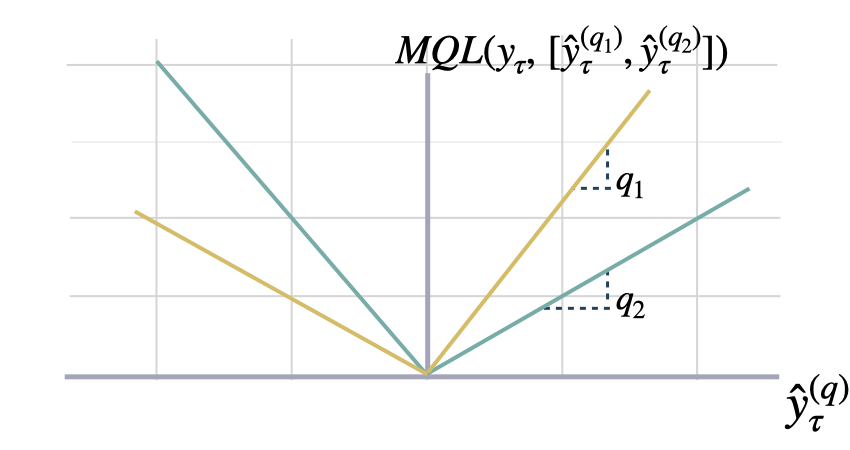

示例和验证

import unittest
import torch as t 
import numpy as np

from neuralforecast.losses.pytorch import (
    MAE, MSE, RMSE,      # 未缩放误差
    MAPE, SMAPE,         # 百分比误差
    MASE,                # 比例误差
    QuantileLoss, MQLoss # 概率误差
)

from neuralforecast.losses.numpy import (
    mae, mse, rmse,              # 未缩放误差
    mape, smape,                 # 百分比误差
    mase,                        # 比例误差
    quantile_loss, mqloss        # 概率误差
)

# 用于测试pytorch/numpy损失函数的测试类
class TestLoss(unittest.TestCase):
    def setUp(self):   
        self.num_quantiles = np.random.randint(3, 10)
        self.first_num = np.random.randint(1, 300)
        self.second_num = np.random.randint(1, 300)
        
        self.y = t.rand(self.first_num, self.second_num)
        self.y_hat = t.rand(self.first_num, self.second_num)
        self.y_hat2 = t.rand(self.first_num, self.second_num)
        self.y_hat_quantile = t.rand(self.first_num, self.second_num, self.num_quantiles)
        
        self.quantiles = t.rand(self.num_quantiles)
        self.q_float = np.random.random_sample()

    def test_mae(self):
        mae_numpy   = mae(self.y, self.y_hat)
        mae_pytorch = MAE()
        mae_pytorch = mae_pytorch(self.y, self.y_hat).numpy()
        self.assertAlmostEqual(mae_numpy, mae_pytorch, places=6)

    def test_mse(self):
        mse_numpy   = mse(self.y, self.y_hat)
        mse_pytorch = MSE()
        mse_pytorch = mse_pytorch(self.y, self.y_hat).numpy()
        self.assertAlmostEqual(mse_numpy, mse_pytorch, places=6)

    def test_rmse(self):
        rmse_numpy   = rmse(self.y, self.y_hat)
        rmse_pytorch = RMSE()
        rmse_pytorch = rmse_pytorch(self.y, self.y_hat).numpy()
        self.assertAlmostEqual(rmse_numpy, rmse_pytorch, places=6)

    def test_mape(self):
        mape_numpy   = mape(y=self.y, y_hat=self.y_hat)
        mape_pytorch = MAPE()
        mape_pytorch = mape_pytorch(y=self.y, y_hat=self.y_hat).numpy()
        self.assertAlmostEqual(mape_numpy, mape_pytorch, places=6)

    def test_smape(self):
        smape_numpy   = smape(self.y, self.y_hat)
        smape_pytorch = SMAPE()
        smape_pytorch = smape_pytorch(self.y, self.y_hat).numpy()
        self.assertAlmostEqual(smape_numpy, smape_pytorch, places=4)
    
    #定义测试mase的方法(self):
    # y_insample = t.rand(self.first_num, self.second_num)
    # 季节性 = 24
    # 每小时24次，每日7次，每周52次
    # 每月12次，每季度4次，每年1次
    # mase_numpy = mase(y=self.y, y_hat=self.y_hat,
    # y_insample=y_insample, 季节性=季节性)
    # mase_object = MASE(seasonality=seasonality)
    # mase_pytorch = mase_对象(y=self.y, y_hat=self.y_hat,
    # y_insample=y_insample).numpy()
    # self.assertAlmostEqual(mase_numpy, mase_pytorch, places=2)

    #定义测试相对平均绝对误差的方法(self):
    # rmae_numpy = rmae(self.y, self.y_hat, self.y_hat2)
    # rmae_对象 = RMAE()
    # rmae_pytorch = rmae_object(self.y, self.y_hat, self.y_hat2).numpy()
    # self.assertAlmostEqual(rmae_numpy, rmae_pytorch, places=4)

    def test_quantile(self):
        quantile_numpy = quantile_loss(self.y, self.y_hat, q = self.q_float)
        quantile_pytorch = QuantileLoss(q = self.q_float)
        quantile_pytorch = quantile_pytorch(self.y, self.y_hat).numpy()
        self.assertAlmostEqual(quantile_numpy, quantile_pytorch, places=6)
    
    # def test_mqloss(self):
    # weights = np.ones_like(self.y)

    # mql_np_w = mqloss(self.y, self.y_hat_quantile, self.quantiles, weights=weights)
    # mql_np_default_w = mqloss(self.y, self.y_hat_quantile, self.quantiles)

    # mql_object = MQLoss(quantiles=self.quantiles)
    # mql_py_w = mql_object(y=self.y,
    # y_hat=self.y_hat_分位数,
    # mask = t.Tensor(weights).numpy()
        
    #     print('self.y.shape', self.y.shape)
    #     print('self.y_hat_quantile.shape', self.y_hat_quantile.shape)
    # mql_py_default_w = mql_object(y=self.y,
    # y_hat = self.y_hat_quantile).numpy()

    # weights[0,:] = 0
    # mql_np_new_w = mqloss(self.y, self.y_hat_quantile, self.quantiles, weights=weights)
    # mql_py_new_w = mql_object(y=self.y,
    # y_hat=self.y_hat_分位数,
    # mask = t.Tensor(weights).numpy()

    # self.assertAlmostEqual(mql_np_w, mql_np_default_w)
    # self.assertAlmostEqual(mql_py_w, mql_py_default_w)
    # self.assertAlmostEqual(mql_np_new_w, mql_py_new_w)
    

unittest.main(argv=[''], verbosity=2, exit=False)

Give us a ⭐ on Github