from nbdev.showdoc import show_doc
from neuralforecast.losses.pytorch import GMM
from neuralforecast import NeuralForecast
from neuralforecast.models import NHITS
import pandas as pd提示
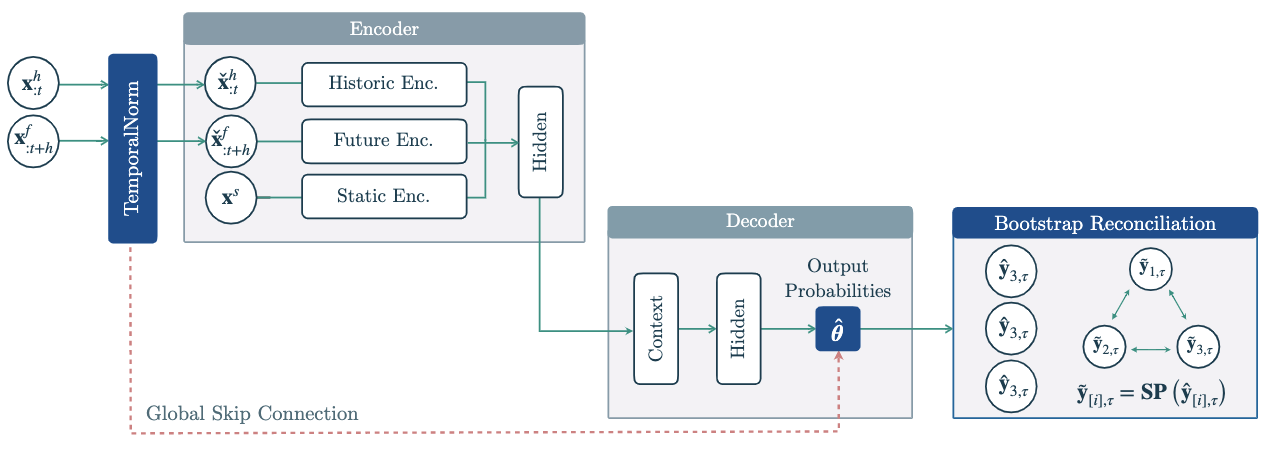
层次混合网络(HINT)是一种高度模块化的框架,将最先进的神经预测架构与任务专用的混合概率和先进的层次协调策略相结合。这种强大的组合使得HINT能够生成准确且一致的概率预测。
HINT将一个 TemporalNorm 模块纳入任何神经预测架构,该模块将输入标准化到网络非线性交互的操作范围,并通过全局跳跃连接重新组合其输出的尺度,从而提高了准确性和训练的稳健性。HINT确保通过自助样本协调恢复聚合约束到其基本样本中,从而保持预测的一致性。
参考文献
- Kin G. Olivares, David Luo, Cristian Challu, Stefania La Vattiata, Max Mergenthaler, Artur Dubrawski (2023). “HINT: Hierarchical Mixture Networks For Coherent Probabilistic Forecasting”. Neural Information Processing Systems, 提交中。工作论文版本可在arxiv上获取。
- Kin G. Olivares, O. Nganba Meetei, Ruijun Ma, Rohan Reddy, Mengfei Cao, Lee Dicker (2022).”Probabilistic Hierarchical Forecasting with Deep Poisson Mixtures”. International Journal Forecasting, 接收的论文可在arxiv上获取。
- Kin G. Olivares, Federico Garza, David Luo, Cristian Challu, Max Mergenthaler, Souhaib Ben Taieb, Shanika Wickramasuriya, and Artur Dubrawski (2022). “HierarchicalForecast: A reference framework for hierarchical forecasting in python”. Journal of Machine Learning Research, 提交中,abs/2207.03517, 2022b.
from typing import Optional
import numpy as np
import torch对账方法
def get_bottomup_P(S: np.ndarray):
"""BottomUp Reconciliation Matrix.
Creates BottomUp hierarchical \"projection\" matrix is defined as:
$$\mathbf{P}_{\\text{BU}} = [\mathbf{0}_{\mathrm{[b],[a]}}\;|\;\mathbf{I}_{\mathrm{[b][b]}}]$$
**Parameters:**<br>
`S`: Summing matrix of size (`base`, `bottom`).<br>
**Returns:**<br>
`P`: Reconciliation matrix of size (`bottom`, `base`).<br>
**References:**<br>
- [Orcutt, G.H., Watts, H.W., & Edwards, J.B.(1968). \"Data aggregation and information loss\". The American
Economic Review, 58 , 773(787)](http://www.jstor.org/stable/1815532).
"""
n_series = len(S)
n_agg = n_series-S.shape[1]
P = np.zeros_like(S)
P[n_agg:,:] = S[n_agg:,:]
P = P.T
return P
def get_mintrace_ols_P(S: np.ndarray):
"""MinTraceOLS Reconciliation Matrix.
Creates MinTraceOLS reconciliation matrix as proposed by Wickramasuriya et al.
$$\mathbf{P}_{\\text{MinTraceOLS}}=\\left(\mathbf{S}^{\intercal}\mathbf{S}\\right)^{-1}\mathbf{S}^{\intercal}$$
**Parameters:**<br>
`S`: Summing matrix of size (`base`, `bottom`).<br>
**Returns:**<br>
`P`: Reconciliation matrix of size (`bottom`, `base`).<br>
**References:**<br>
- [Wickramasuriya, S.L., Turlach, B.A. & Hyndman, R.J. (2020). \"Optimal non-negative
forecast reconciliation". Stat Comput 30, 1167–1182,
https://doi.org/10.1007/s11222-020-09930-0](https://robjhyndman.com/publications/nnmint/).
"""
n_hiers, n_bottom = S.shape
n_agg = n_hiers - n_bottom
W = np.eye(n_hiers)
# 我们计算协调矩阵。
# 来自 https://robjhyndman.com/papers/MinT.pdf 的公式 10
A = S[:n_agg,:]
U = np.hstack((np.eye(n_agg), -A)).T
J = np.hstack((np.zeros((n_bottom,n_agg)), np.eye(n_bottom)))
P = J - (J @ W @ U) @ np.linalg.pinv(U.T @ W @ U) @ U.T
return P
def get_mintrace_wls_P(S: np.ndarray):
"""MinTraceOLS Reconciliation Matrix.
Creates MinTraceOLS reconciliation matrix as proposed by Wickramasuriya et al.
Depending on a weighted GLS estimator and an estimator of the covariance matrix of the coherency errors $\mathbf{W}_{h}$.
$$ \mathbf{W}_{h} = \mathrm{Diag}(\mathbf{S} \mathbb{1}_{[b]})$$
$$\mathbf{P}_{\\text{MinTraceWLS}}=\\left(\mathbf{S}^{\intercal}\mathbf{W}_{h}\mathbf{S}\\right)^{-1}
\mathbf{S}^{\intercal}\mathbf{W}^{-1}_{h}$$
**Parameters:**<br>
`S`: Summing matrix of size (`base`, `bottom`).<br>
**Returns:**<br>
`P`: Reconciliation matrix of size (`bottom`, `base`).<br>
**References:**<br>
- [Wickramasuriya, S.L., Turlach, B.A. & Hyndman, R.J. (2020). \"Optimal non-negative
forecast reconciliation". Stat Comput 30, 1167–1182,
https://doi.org/10.1007/s11222-020-09930-0](https://robjhyndman.com/publications/nnmint/).
"""
n_hiers, n_bottom = S.shape
n_agg = n_hiers - n_bottom
W = np.diag(S @ np.ones((n_bottom,)))
# 我们计算协调矩阵。
# 来自 https://robjhyndman.com/papers/MinT.pdf 的公式 10
A = S[:n_agg,:]
U = np.hstack((np.eye(n_agg), -A)).T
J = np.hstack((np.zeros((n_bottom,n_agg)), np.eye(n_bottom)))
P = J - (J @ W @ U) @ np.linalg.pinv(U.T @ W @ U) @ U.T
return P
def get_identity_P(S: np.ndarray):
# 用于身份P的占位函数(无对账)。
passshow_doc(get_bottomup_P, title_level=3)show_doc(get_mintrace_ols_P, title_level=3)show_doc(get_mintrace_wls_P, title_level=3)提示
class HINT:
""" HINT
The Hierarchical Mixture Networks (HINT) are a highly modular framework that
combines SoTA neural forecast architectures with a task-specialized mixture
probability and advanced hierarchical reconciliation strategies. This powerful
combination allows HINT to produce accurate and coherent probabilistic forecasts.
HINT's incorporates a `TemporalNorm` module into any neural forecast architecture,
the module normalizes inputs into the network's non-linearities operating range
and recomposes its output's scales through a global skip connection, improving
accuracy and training robustness. HINT ensures the forecast coherence via bootstrap
sample reconciliation that restores the aggregation constraints into its base samples.
Available reconciliations:<br>
- BottomUp<br>
- MinTraceOLS<br>
- MinTraceWLS<br>
- Identity
**Parameters:**<br>
`h`: int, Forecast horizon. <br>
`model`: NeuralForecast model, instantiated model class from [architecture collection](https://nixtla.github.io/neuralforecast/models.pytorch.html).<br>
`S`: np.ndarray, dumming matrix of size (`base`, `bottom`) see HierarchicalForecast's [aggregate method](https://nixtla.github.io/hierarchicalforecast/utils.html#aggregate).<br>
`reconciliation`: str, HINT's reconciliation method from ['BottomUp', 'MinTraceOLS', 'MinTraceWLS'].<br>
`alias`: str, optional, Custom name of the model.<br>
"""
def __init__(self,
h: int,
S: np.ndarray,
model,
reconciliation: str,
alias: Optional[str] = None):
if model.h != h:
raise Exception(f"Model h {model.h} does not match HINT h {h}")
if not model.loss.is_distribution_output:
raise Exception(f"The NeuralForecast model's loss {model.loss} is not a probabilistic objective")
self.h = h
self.model = model
self.early_stop_patience_steps = model.early_stop_patience_steps
self.S = S
self.reconciliation = reconciliation
self.loss = model.loss
available_reconciliations = dict(
BottomUp=get_bottomup_P,
MinTraceOLS=get_mintrace_ols_P,
MinTraceWLS=get_mintrace_wls_P,
Identity=get_identity_P,
)
if reconciliation not in available_reconciliations:
raise Exception(f"Reconciliation {reconciliation} not available")
# 获取SP矩阵
self.reconciliation = reconciliation
if reconciliation== 'Identity':
self.SP = None
else:
P = available_reconciliations[reconciliation](S=S)
self.SP = S @ P
qs = torch.Tensor((np.arange(self.loss.num_samples)/self.loss.num_samples))
self.sample_quantiles = torch.nn.Parameter(qs, requires_grad=False)
self.alias = alias
def __repr__(self):
return type(self).__name__ if self.alias is None else self.alias
def fit(self, dataset, val_size=0, test_size=0, random_seed=None, distributed_config=None):
""" HINT.fit
HINT trains on the entire hierarchical dataset, by minimizing a composite log likelihood objective.
HINT framework integrates `TemporalNorm` into the neural forecast architecture for a scale-decoupled
optimization that robustifies cross-learning the hierachy's series scales.
**Parameters:**<br>
`dataset`: NeuralForecast's `TimeSeriesDataset` see details [here](https://nixtla.github.io/neuralforecast/tsdataset.html)<br>
`val_size`: int, size of the validation set, (default 0).<br>
`test_size`: int, size of the test set, (default 0).<br>
`random_seed`: int, random seed for the prediction.<br>
**Returns:**<br>
`self`: A fitted base `NeuralForecast` model.<br>
"""
model = self.model.fit(dataset=dataset,
val_size=val_size,
test_size=test_size,
random_seed=random_seed,
distributed_config=distributed_config)
# 增加了与NeuralForecast核心兼容的属性
self.futr_exog_list = self.model.futr_exog_list
self.hist_exog_list = self.model.hist_exog_list
self.stat_exog_list = self.model.stat_exog_list
return model
def predict(self, dataset, step_size=1, random_seed=None, **data_module_kwargs):
""" HINT.predict
After fitting a base model on the entire hierarchical dataset.
HINT restores the hierarchical aggregation constraints using
bootstrapped sample reconciliation.
**Parameters:**<br>
`dataset`: NeuralForecast's `TimeSeriesDataset` see details [here](https://nixtla.github.io/neuralforecast/tsdataset.html)<br>
`step_size`: int, steps between sequential predictions, (default 1).<br>
`random_seed`: int, random seed for the prediction.<br>
`**data_kwarg`: additional parameters for the dataset module.<br>
**Returns:**<br>
`y_hat`: numpy predictions of the `NeuralForecast` model.<br>
"""
# Non-reconciled predictions
if self.reconciliation=='Identity':
forecasts = self.model.predict(dataset=dataset,
step_size=step_size,
random_seed=random_seed,
**data_module_kwargs)
return forecasts
num_samples = self.model.loss.num_samples
# Hack to get samples by simulating quantiles (samples will be ordered)
# Mysterious parsing associated to default [mean,quantiles] output
quantiles_old = self.model.loss.quantiles
names_old = self.model.loss.output_names
self.model.loss.quantiles = self.sample_quantiles
self.model.loss.output_names = ['1'] * (1 + num_samples)
samples = self.model.predict(dataset=dataset,
step_size=step_size,
random_seed=random_seed,
**data_module_kwargs)
samples = samples[:,1:] # Eliminate mean from quantiles
self.model.loss.quantiles = quantiles_old
self.model.loss.output_names = names_old
# Hack requires to break quantiles correlations between samples
idxs = np.random.choice(num_samples, size=samples.shape, replace=True)
aux_col_idx = np.arange(len(samples))[:,None] * num_samples
idxs = idxs + aux_col_idx
samples = samples.flatten()[idxs]
samples = samples.reshape(dataset.n_groups, -1, self.h, num_samples)
# Bootstrap Sample Reconciliation
# Default output [mean, quantiles]
samples = np.einsum('ij, jwhp -> iwhp', self.SP, samples)
sample_mean = np.mean(samples, axis=-1, keepdims=True)
sample_mean = sample_mean.reshape(-1, 1)
forecasts = np.quantile(samples, self.model.loss.quantiles, axis=-1)
forecasts = forecasts.transpose(1,2,3,0) # [...,samples]
forecasts = forecasts.reshape(-1, len(self.model.loss.quantiles))
forecasts = np.concatenate([sample_mean, forecasts], axis=-1)
return forecasts
def set_test_size(self, test_size):
self.model.test_size = test_size
def get_test_size(self):
return self.model.test_size
def save(self, path):
""" HINT.save
将HINT拟合模型保存到磁盘。
**参数:**<br>
`path`: str, 保存模型的路径。<br>
"""
self.model.save(path)show_doc(HINT, title_level=3)show_doc(HINT.fit, title_level=3)show_doc(HINT.predict, title_level=3)::: {#cell-17 .cell 0=‘隐’ 1=‘藏’}
# 单元测试以检查层次一致性
# 概率相干 => 样本相干 => 平均相干
def sort_df_hier(Y_df, S_df):
# NeuralForecast 核心,按字典顺序对 unique_id 进行排序
# 默认情况下,此类会匹配 S_df 和 Y_hat_df 的顺序。
Y_df.unique_id = Y_df.unique_id.astype('category')
Y_df.unique_id = Y_df.unique_id.cat.set_categories(S_df.index)
Y_df = Y_df.sort_values(by=['unique_id', 'ds'])
return Y_df
# -----创建合成数据集-----
np.random.seed(123)
train_steps = 20
num_levels = 7
level = np.arange(0, 100, 0.1)
qs = [[50-lv/2, 50+lv/2] for lv in level]
quantiles = np.sort(np.concatenate(qs)/100)
levels = ['Top', 'Mid1', 'Mid2', 'Bottom1', 'Bottom2', 'Bottom3', 'Bottom4']
unique_ids = np.repeat(levels, train_steps)
S = np.array([[1., 1., 1., 1.],
[1., 1., 0., 0.],
[0., 0., 1., 1.],
[1., 0., 0., 0.],
[0., 1., 0., 0.],
[0., 0., 1., 0.],
[0., 0., 0., 1.]])
S_dict = {col: S[:, i] for i, col in enumerate(levels[3:])}
S_df = pd.DataFrame(S_dict, index=levels)
ds = pd.date_range(start='2018-03-31', periods=train_steps, freq='Q').tolist() * num_levels
# 创建Y_df
y_lists = [S @ np.random.uniform(low=100, high=500, size=4) for i in range(train_steps)]
y = [elem for tup in zip(*y_lists) for elem in tup]
Y_df = pd.DataFrame({'unique_id': unique_ids, 'ds': ds, 'y': y})
Y_df = sort_df_hier(Y_df, S_df)
# ------拟合/预测 HINT 模型------
# 模型 + 分布 + 协调
nhits = NHITS(h=4,
input_size=4,
loss=GMM(n_components=2, quantiles=quantiles, num_samples=len(quantiles)),
max_steps=5,
early_stop_patience_steps=2,
val_check_steps=1,
scaler_type='robust',
learning_rate=1e-3)
model = HINT(h=4, model=nhits, S=S, reconciliation='BottomUp')
# 拟合与预测
nf = NeuralForecast(models=[model], freq='Q')
forecasts = nf.cross_validation(df=Y_df, val_size=4, n_windows=1)
# ---检查层级一致性---
parent_children_dict = {0: [1, 2], 1: [3, 4], 2: [5, 6]}
# 检查每个地平时间步的连贯性
for _, df in forecasts.groupby('ds'):
hint_mean = df['HINT'].values
for parent_idx, children_list in parent_children_dict.items():
parent_value = hint_mean[parent_idx]
children_sum = hint_mean[children_list].sum()
np.testing.assert_allclose(children_sum, parent_value, rtol=1e-6):::
使用示例
在这个例子中,我们将使用HINT进行层次预测任务,这是一个具有聚合约束的多变量回归问题。聚合约束可以通过求和矩阵 \(\mathbf{S}_{[i][b]}\) 进行紧凑表示,下面的图展示了一个示例。
在这个例子中,我们将为TourismL数据集做出一致的预测。
大纲
1. 导入包
2. 加载层次数据集
3. 拟合和预测HINT
4. 预测图

import matplotlib.pyplot as plt
from neuralforecast.losses.pytorch import GMM, sCRPS
from datasetsforecast.hierarchical import HierarchicalData
# 辅助排序
def sort_df_hier(Y_df, S_df):
# NeuralForecast 核心,按字典顺序对 unique_id 进行排序
# 默认情况下,此类会匹配 S_df 和 Y_hat_df 的顺序。
Y_df.unique_id = Y_df.unique_id.astype('category')
Y_df.unique_id = Y_df.unique_id.cat.set_categories(S_df.index)
Y_df = Y_df.sort_values(by=['unique_id', 'ds'])
return Y_df
# 负载旅游小数据集
horizon = 12
Y_df, S_df, tags = HierarchicalData.load('./data', 'TourismLarge')
Y_df['ds'] = pd.to_datetime(Y_df['ds'])
Y_df = sort_df_hier(Y_df, S_df)
level = [80,90]
# 实例化HINT
# 基础网络 + 分发 + 对账
nhits = NHITS(h=horizon,
input_size=24,
loss=GMM(n_components=10, level=level),
max_steps=2000,
early_stop_patience_steps=10,
val_check_steps=50,
scaler_type='robust',
learning_rate=1e-3,
valid_loss=sCRPS(level=level))
model = HINT(h=horizon, S=S_df.values,
model=nhits, reconciliation='BottomUp')
# 拟合与预测
nf = NeuralForecast(models=[model], freq='MS')
Y_hat_df = nf.cross_validation(df=Y_df, val_size=12, n_windows=1)
Y_hat_df = Y_hat_df.reset_index()# 情节连贯的概率预测
unique_id = 'TotalAll'
Y_plot_df = Y_df[Y_df.unique_id==unique_id]
plot_df = Y_hat_df[Y_hat_df.unique_id==unique_id]
plot_df = Y_plot_df.merge(plot_df, on=['ds', 'unique_id'], how='left')
n_years = 5
plt.plot(plot_df['ds'][-12*n_years:], plot_df['y_x'][-12*n_years:], c='black', label='True')
plt.plot(plot_df['ds'][-12*n_years:], plot_df['HINT'][-12*n_years:], c='purple', label='mean')
plt.plot(plot_df['ds'][-12*n_years:], plot_df['HINT-median'][-12*n_years:], c='blue', label='median')
plt.fill_between(x=plot_df['ds'][-12*n_years:],
y1=plot_df['HINT-lo-90'][-12*n_years:].values,
y2=plot_df['HINT-hi-90'][-12*n_years:].values,
alpha=0.4, label='level 90')
plt.legend()
plt.grid()
plt.plot()Give us a ⭐ on Github