稳健预测

当数据集中存在离群值时，它们可能会干扰计算的摘要统计量，例如均值和标准差，导致模型偏向离群值并偏离大多数观测值。因此，模型在准确适应离群值和在正常数据上表现良好之间需要取得平衡，从而提高在这两种数据类型上的整体性能。鲁棒回归算法 解决了这个问题，明确考虑了数据集中的离群值。

在本笔记本中，我们将展示如何拟合鲁棒的 NeuralForecast 方法。我们将会：
- 安装 NeuralForecast。
- 加载带噪声的 AirPassengers 数据集。
- 拟合并预测鲁棒化的 NeuralForecast。
- 绘制并评估预测结果。

您可以使用 Google Colab 在 GPU 上运行这些实验。

在 Colab 中打开

1. 安装 NeuralForecast

%%capture
!pip install git+https://github.com/Nixtla/neuralforecast.git
import numpy as np
import pandas as pd
from sklearn import datasets

import matplotlib.pyplot as plt
from random import random
from random import randint
from random import seed

from neuralforecast import NeuralForecast
from neuralforecast.utils import AirPassengersDF

from neuralforecast.models import NHITS
from neuralforecast.losses.pytorch import MQLoss, DistributionLoss, HuberMQLoss

from neuralforecast.losses.numpy import mape, mqloss

2. 加载噪声的航空乘客数据

在这个例子中，我们将使用经典的Box-Cox航空乘客数据集，并通过引入异常值来增强它。

具体来说，我们将重点引入异常值到目标变量，通过指定的因素（如2到4倍的标准差）来使其偏离原始观测值。

# 原始的Box-Cox转换后的AirPassengers数据 
# 如神经预测工具包中所定义
Y_df = AirPassengersDF.copy() 
plt.plot(Y_df.y)
plt.ylabel('Monthly Passengers')
plt.xlabel('Timestamp [t]')
plt.grid()

# 在这里，我们向AirPassengers数据中添加了一些人工异常值。
seed(1)
for i in range(len(Y_df)):
    factor = randint(2, 4)
    if random() > 0.97:
        Y_df.y[i] += factor * Y_df.y.std()

plt.plot(Y_df.y)
plt.ylabel('Monthly Passengers + Noise')
plt.xlabel('Timestamp [t]')
plt.grid()

# 将数据集划分为训练集和测试集 
# 过去12个月的测试
Y_train_df = Y_df.groupby('unique_id').head(-12).reset_index()
Y_test_df = Y_df.groupby('unique_id').tail(12).reset_index()
Y_test_df
index unique_id ds y
0 132 1.0 1960-01-31 417.0
1 133 1.0 1960-02-29 391.0
2 134 1.0 1960-03-31 419.0
3 135 1.0 1960-04-30 461.0
4 136 1.0 1960-05-31 472.0
5 137 1.0 1960-06-30 535.0
6 138 1.0 1960-07-31 622.0
7 139 1.0 1960-08-31 606.0
8 140 1.0 1960-09-30 508.0
9 141 1.0 1960-10-31 461.0
10 142 1.0 1960-11-30 390.0
11 143 1.0 1960-12-31 432.0

3. 拟合和预测稳健化的NeuralForecast

Huber MQ 损失

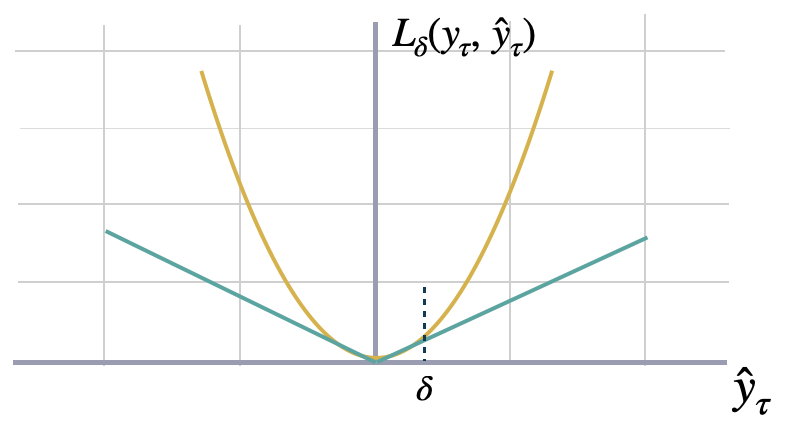
Huber 损失用于稳健回归，是一种损失函数，与平方误差损失相比，对数据中的异常值表现出较低的敏感性。Huber 损失函数对小误差是二次的，对大误差是线性的。在这里，我们将对其进行轻微的修改，以适用于概率预测。请随意调整 \(\delta\) 参数。

Dropout正则化

Dropout技术是一种用于神经网络的正则化方法，旨在防止过拟合。在训练过程中，dropout会随机将每次更新中一层的输入单元或神经元的一部分设置为零，有效地“丢弃”这些单元。这意味着网络不能依赖任何单个单元，因为它可能在任何时候被丢弃。通过这样做，dropout迫使网络学习更强健和更具可泛化性的表示，防止单元之间过度共适应。

Dropout方法可以帮助我们增强网络对自回归特征中异常值的鲁棒性。您可以通过dropout_prob_theta参数进行探讨。

适配NeuralForecast模型

使用 NeuralForecast.fit 方法，你可以为你的数据集训练一组模型。你可以定义预测的 horizon（在这个例子中为 12），并修改模型的超参数。例如，对于 NHITS，我们将编码器和解码器的默认隐藏大小进行了更改。

请参阅 NHITS 和 MLP 模型文档。

%%capture
horizon = 12
quantiles = [0.1, 0.25, 0.5, 0.75, 0.9]

# 尝试不同的超参数以提高准确性。
models = [NHITS(h=horizon,                           # 预测范围
                input_size=2 * horizon,              # 输入序列的长度
                loss=HuberMQLoss(quantiles=quantiles),    # 鲁棒的Huber损失
                valid_loss=MQLoss(quantiles=quantiles),   # 验证信号
                max_steps=500,                       # 训练步骤数
                dropout_prob_theta=0.6,              # 丢弃以增强鲁棒性 vs 异常滞后输入
                #早停耐心步数=2,        # Early stopping regularization patience
                val_check_steps=10,                  # 验证信号的频率（影响提前停止）
                alias='Huber',
              ),
          NHITS(h=horizon,
                input_size=2 * horizon,
                loss=DistributionLoss(distribution='Normal', 
                                      quantiles=quantiles), # 经典正态分布
                valid_loss=MQLoss(quantiles=quantiles),
                max_steps=500,
                #早停耐心步数=2,
                dropout_prob_theta=0.6,
                val_check_steps=10,
                alias='Normal',
              )
          ]
nf = NeuralForecast(models=models, freq='M')
nf.fit(df=Y_train_df)
Y_hat_df = nf.predict()
Global seed set to 1
Global seed set to 1
# 默认情况下，NeuralForecast 生成预测区间
# 在这种情况下，低x和高x水平代表 
# 预测累积x%概率的上下限
Y_hat_df = Y_hat_df.reset_index(drop=True)
Y_hat_df
ds Huber-lo-80.0 Huber-lo-50.0 Huber-median Huber-hi-50.0 Huber-hi-80.0 Normal Normal-lo-80.0 Normal-lo-50.0 Normal-median Normal-hi-50.0 Normal-hi-80.0
0 1960-01-31 392.046448 397.029694 402.842377 412.451111 420.441254 370.554321 -1246.564331 -466.951233 374.260681 1214.356934 1953.910645
1 1960-02-29 389.217041 398.078979 411.310669 426.811432 462.116272 431.134827 -1016.146179 -376.702576 469.389313 1195.809082 1874.808838
2 1960-03-31 434.787323 446.318176 456.515533 468.646667 486.479950 469.221069 -965.224670 -268.812164 455.846985 1197.529175 1983.282349
3 1960-04-30 435.589081 443.395844 451.102966 458.542328 469.953857 544.345642 -1038.976440 -251.178711 535.880615 1403.179932 2100.239990
4 1960-05-31 442.144714 448.320862 455.896271 466.212524 477.713348 400.593628 -1188.452881 -417.007935 426.566284 1202.106201 2103.583008
5 1960-06-30 505.597168 513.204590 522.992188 535.911987 547.264099 482.142883 -1210.700195 -386.704407 484.923767 1400.397339 2142.133789
6 1960-07-31 566.634033 576.086548 588.730164 602.847534 613.312256 548.551086 -1049.558838 -299.192017 578.715820 1399.025879 2226.514404
7 1960-08-31 554.081116 568.410767 580.600281 594.198730 605.851440 542.382874 -1056.719116 -310.321533 543.106689 1420.388306 2138.160889
8 1960-09-30 503.825928 511.493469 520.782532 530.070435 551.331299 656.870056 -957.937927 -157.202362 644.464355 1539.134644 2261.052490
9 1960-10-31 438.602539 445.856720 454.243591 462.382782 487.070221 662.375427 -926.544312 -206.266907 650.127808 1537.292480 2253.246094
10 1960-11-30 395.615570 402.616699 417.529083 430.389435 452.758911 499.940247 -1233.157471 -397.680908 492.310120 1396.803711 2209.155273
11 1960-12-31 433.402496 439.153748 448.741119 456.206573 471.018433 458.918365 -1393.779053 -589.960815 468.123871 1448.744263 2284.202637

4. 绘制并评估预测结果

最后，我们将两种模型的预测值与真实值进行绘制。

并评估 NHITS-Huber 和 NHITS-Normal 预测器的准确性。

fig, ax = plt.subplots(1, 1, figsize = (20, 7))
plot_df = pd.concat([Y_train_df, Y_hat_df]).set_index('ds') # 连接训练和预测数据框
plot_df[['y', 'Huber-median', 'Normal-median']].plot(ax=ax, linewidth=2)

ax.set_title('Noisy AirPassengers Forecast', fontsize=22)
ax.set_ylabel('Monthly Passengers', fontsize=20)
ax.set_xlabel('Timestamp [t]', fontsize=20)
ax.legend(prop={'size': 15})
ax.grid()

为了评估中位数预测，我们使用平均百分比误差（MAPE），定义如下：

\[\mathrm{MAPE}(\mathbf{y}_{\tau}, \hat{\mathbf{y}}_{\tau}) = \mathrm{mean}\left(\frac{|\mathbf{y}_{\tau}-\hat{\mathbf{y}}_{\tau}|}{|\mathbf{y}_{\tau}|}\right)\]

#来自neuralforecast.losses.numpy模块的mape和mqloss函数

huber_mae = mape(y=Y_test_df['y'], y_hat=Y_hat_df['Huber-median'])
normal_mae = mape(y=Y_test_df['y'], y_hat=Y_hat_df['Normal-median'])

print(f'Huber MAPE: {huber_mae:.1%}')
print(f'Normal MAPE: {normal_mae:.1%}')
Huber MAPE: 4.2%
Normal MAPE: 16.2%

为了评估相干的概率预测，我们使用连续排名概率得分（CRPS），其定义如下：

\[\mathrm{CRPS}(\hat{F}_{\tau},\mathbf{y}_{\tau}) = \int^{1}_{0} \mathrm{QL}(\hat{F}_{\tau}, y_{\tau})_{q} dq\]

正如您所看到的，稳健回归的改进也可以反映在概率预测中。

huber_qcols = ['Huber-lo-80.0', 'Huber-lo-50.0',    'Huber-median', 'Huber-hi-50.0', 'Huber-hi-80.0']
normal_qcols = ['Normal-lo-80.0', 'Normal-lo-50.0', 'Normal-median',    'Normal-hi-50.0', 'Normal-hi-80.0']

huber_crps = mqloss(y=Y_test_df['y'], y_hat=Y_hat_df[huber_qcols], 
                   quantiles=np.array(quantiles))
normal_crps = mqloss(y=Y_test_df['y'], y_hat=Y_hat_df[normal_qcols], 
                    quantiles=np.array(quantiles))

print(f'Huber CRPS: {huber_crps:.4}')
print(f'Normal CRPS: {normal_crps:.4}')
Huber CRPS: 6.139
Normal CRPS: 157.5

参考文献

Give us a ⭐ on Github