from typing import Tuple, Optional
import torch
import torch.nn as nn
import torch.nn.functional as F
from torch import Tensor
from torch.nn import LayerNorm
import pandas as pd
from neuralforecast.losses.pytorch import MAE
from neuralforecast.common._base_windows import BaseWindowsTFT
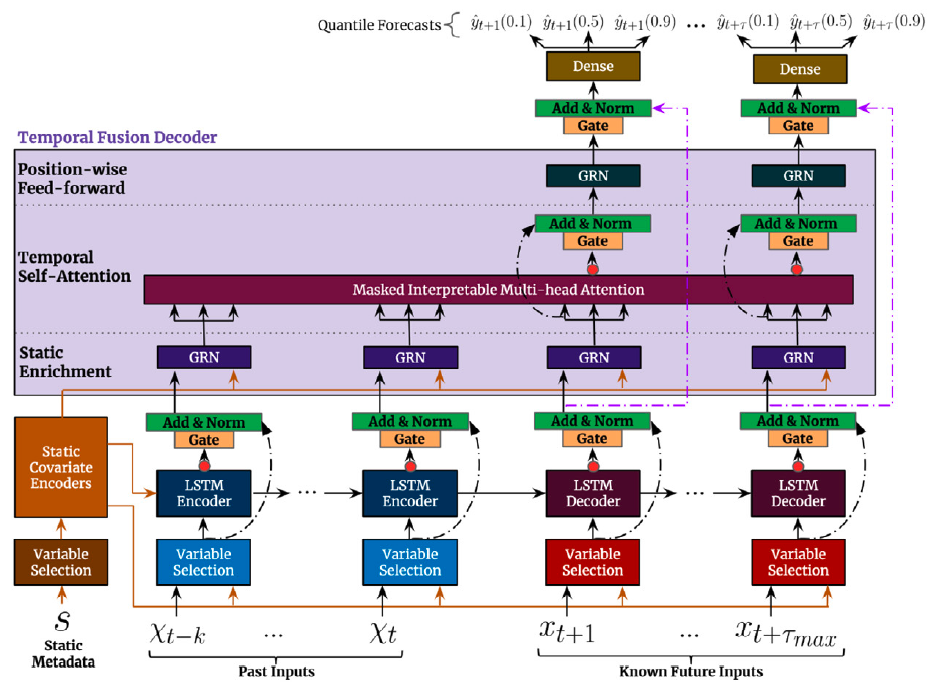
总之,时间融合变换器(TFT)结合了门控层、LSTM递归编码器和多头注意力层,形成了一种多步预测策略解码器。
TFT的输入包括静态外生变量 \(\mathbf{x}^{(s)}\)、历史外生变量 \(\mathbf{x}^{(h)}_{[:t]}\)、预测时可用的外生变量 \(\mathbf{x}^{(f)}_{[:t+H]}\) 和自回归特征 \(\mathbf{y}_{[:t]}\),这些输入进一步分解为分类和连续特征。该网络使用多量纲回归来建模以下条件概率:\[\mathbb{P}(\mathbf{y}_{[t+1:t+H]}|\;\mathbf{y}_{[:t]},\; \mathbf{x}^{(h)}_{[:t]},\; \mathbf{x}^{(f)}_{[:t+H]},\; \mathbf{x}^{(s)})\]
参考文献
- Jan Golda, Krzysztof Kudrynski. “NVIDIA, 深度学习预测示例”
- Bryan Lim, Sercan O. Arik, Nicolas Loeff, Tomas Pfister, “时间融合变换器用于可解释的多视野时间序列预测”
import logging
import warnings
from fastcore.test import test_eq
from nbdev.showdoc import show_doclogging.getLogger("pytorch_lightning").setLevel(logging.ERROR)
warnings.filterwarnings("ignore")1. 辅助函数
1.1 门控机制
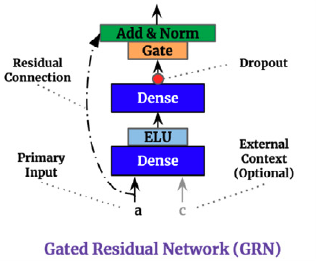
门控残差网络(GRN)提供了自适应的深度和网络复杂性,能够适应不同大小的数据集。由于残差连接允许网络跳过输入 \(\mathbf{a}\) 和上下文 \(\mathbf{c}\) 的非线性变换。
\[\begin{align} \eta_{1} &= \mathrm{ELU}(\mathbf{W}_{1}\mathbf{a}+\mathbf{W}_{2}\mathbf{c}+\mathbf{b}_{1}) \\ \eta_{2} &= \mathbf{W}_{2}\eta_{1}+b_{2} \\ \mathrm{GRN}(\mathbf{a}, \mathbf{c}) &= \mathrm{LayerNorm}(a + \textrm{GLU}(\eta_{2})) \end{align}\]
门控线性单元(GLU)提供了抑制 GRN 中不必要部分的灵活性。考虑 GRN 的输出 \(\gamma\),那么 GLU 变换定义为:
\[\mathrm{GLU}(\gamma) = \sigma(\mathbf{W}_{4}\gamma +b_{4}) \odot (\mathbf{W}_{5}\gamma +b_{5})\]
class MaybeLayerNorm(nn.Module):
def __init__(self, output_size, hidden_size, eps):
super().__init__()
if output_size and output_size == 1:
self.ln = nn.Identity()
else:
self.ln = LayerNorm(output_size if output_size else hidden_size,
eps=eps)
def forward(self, x):
return self.ln(x)
class GLU(nn.Module):
def __init__(self, hidden_size, output_size):
super().__init__()
self.lin = nn.Linear(hidden_size, output_size * 2)
def forward(self, x: Tensor) -> Tensor:
x = self.lin(x)
x = F.glu(x)
return x
class GRN(nn.Module):
def __init__(self,
input_size,
hidden_size,
output_size=None,
context_hidden_size=None,
dropout=0):
super().__init__()
self.layer_norm = MaybeLayerNorm(output_size, hidden_size, eps=1e-3)
self.lin_a = nn.Linear(input_size, hidden_size)
if context_hidden_size is not None:
self.lin_c = nn.Linear(context_hidden_size, hidden_size, bias=False)
self.lin_i = nn.Linear(hidden_size, hidden_size)
self.glu = GLU(hidden_size, output_size if output_size else hidden_size)
self.dropout = nn.Dropout(dropout)
self.out_proj = nn.Linear(input_size, output_size) if output_size else None
def forward(self, a: Tensor, c: Optional[Tensor] = None):
x = self.lin_a(a)
if c is not None:
x = x + self.lin_c(c).unsqueeze(1)
x = F.elu(x)
x = self.lin_i(x)
x = self.dropout(x)
x = self.glu(x)
y = a if not self.out_proj else self.out_proj(a)
x = x + y
x = self.layer_norm(x)
return x1.2 变量选择网络
TFT 通过其变量选择网络 (VSN) 组件包含自动变量选择能力。VSN 接收原始输入 \(\{\mathbf{x}^{(s)}, \mathbf{x}^{(h)}_{[:t]}, \mathbf{x}^{(f)}_{[:t]}\}\),并通过嵌入或线性变换将其转换到高维空间 \(\{\mathbf{E}^{(s)}, \mathbf{E}^{(h)}_{[:t]}, \mathbf{E}^{(f)}_{[:t+H]}\}\)。
对于观察到的历史数据,时间 \(t\) 时的嵌入矩阵 \(\mathbf{E}^{(h)}_{t}\) 是 \(j\) 个变量 \(e^{(h)}_{t,j}\) 嵌入的连接: \[\begin{align} \mathbf{E}^{(h)}_{t} &= [e^{(h)}_{t,1},\dots,e^{(h)}_{t,j},\dots,e^{(h)}_{t,n_{h}}] \\ \mathbf{\tilde{e}}^{(h)}_{t,j} &= \mathrm{GRN}(e^{(h)}_{t,j}) \end{align}\]
变量选择权重由以下公式给出: \[s^{(h)}_{t}=\mathrm{SoftMax}(\mathrm{GRN}(\mathbf{E}^{(h)}_{t},\mathbf{E}^{(s)}))\]
然后处理后的 VSN 特征为: \[\tilde{\mathbf{E}}^{(h)}_{t}= \sum_{j} s^{(h)}_{j} \tilde{e}^{(h)}_{t,j}\]

class TFTEmbedding(nn.Module):
def __init__(self, hidden_size, stat_input_size, futr_input_size, hist_input_size, tgt_size):
super().__init__()
# 输入类型有四种:
# 1. 静态连续
# 2. 先验已知的时间连续性
# 3. 时间观察连续性
# 4. 时间观察目标(迄今为止的时间序列观察结果)
self.hidden_size = hidden_size
self.stat_input_size = stat_input_size
self.futr_input_size = futr_input_size
self.hist_input_size = hist_input_size
self.tgt_size = tgt_size
# 如果大小不为None,则实例化连续嵌入。
for attr, size in [('stat_exog_embedding', stat_input_size),
('futr_exog_embedding', futr_input_size),
('hist_exog_embedding', hist_input_size),
('tgt_embedding', tgt_size)]:
if size:
vectors = nn.Parameter(torch.Tensor(size, hidden_size))
bias = nn.Parameter(torch.zeros(size, hidden_size))
torch.nn.init.xavier_normal_(vectors)
setattr(self, attr+'_vectors', vectors)
setattr(self, attr+'_bias', bias)
else:
setattr(self, attr+'_vectors', None)
setattr(self, attr+'_bias', None)
def _apply_embedding(self,
cont: Optional[Tensor],
cont_emb: Tensor,
cont_bias: Tensor,
):
if (cont is not None):
#下面的代码等价于以下einsums
#e_cont = torch.einsum('btf,fh->bthf', cont, cont_emb)
#e_cont = torch.einsum('bf,fh->bhf', cont, cont_emb)
e_cont = torch.mul(cont.unsqueeze(-1), cont_emb)
e_cont = e_cont + cont_bias
return e_cont
return None
def forward(self, target_inp,
stat_exog=None, futr_exog=None, hist_exog=None):
# 时间/静态 分类/连续 已知/观察到的 输入
# 尝试获取输入,如果失败则返回None。
# 静态输入在所有时间步长中应保持一致。
# 为了提高内存效率,没有使用断言语句。
stat_exog = stat_exog[:,:] if stat_exog is not None else None
s_inp = self._apply_embedding(cont=stat_exog,
cont_emb=self.stat_exog_embedding_vectors,
cont_bias=self.stat_exog_embedding_bias)
k_inp = self._apply_embedding(cont=futr_exog,
cont_emb=self.futr_exog_embedding_vectors,
cont_bias=self.futr_exog_embedding_bias)
o_inp = self._apply_embedding(cont=hist_exog,
cont_emb=self.hist_exog_embedding_vectors,
cont_bias=self.hist_exog_embedding_bias)
# 时间观测目标
# t_observed_tgt = torch.einsum('btf,fh->btfh',
# 目标输入, 自目标嵌入向量)
target_inp = torch.matmul(target_inp.unsqueeze(3).unsqueeze(4),
self.tgt_embedding_vectors.unsqueeze(1)).squeeze(3)
target_inp = target_inp + self.tgt_embedding_bias
return s_inp, k_inp, o_inp, target_inp
class VariableSelectionNetwork(nn.Module):
def __init__(self, hidden_size, num_inputs, dropout):
super().__init__()
self.joint_grn = GRN(input_size=hidden_size*num_inputs,
hidden_size=hidden_size,
output_size=num_inputs,
context_hidden_size=hidden_size)
self.var_grns = nn.ModuleList(
[GRN(input_size=hidden_size,
hidden_size=hidden_size, dropout=dropout)
for _ in range(num_inputs)])
def forward(self, x: Tensor, context: Optional[Tensor] = None):
Xi = x.reshape(*x.shape[:-2], -1)
grn_outputs = self.joint_grn(Xi, c=context)
sparse_weights = F.softmax(grn_outputs, dim=-1)
transformed_embed_list = [m(x[...,i,:])
for i, m in enumerate(self.var_grns)]
transformed_embed = torch.stack(transformed_embed_list, dim=-1)
#下面这行代码执行批量矩阵向量乘法
#for temporal features it's bthf,btf->bth
#for static features it's bhf,bf->bh
variable_ctx = torch.matmul(transformed_embed,
sparse_weights.unsqueeze(-1)).squeeze(-1)
return variable_ctx, sparse_weights1.3. 多头注意力
为了避免经典Seq2Seq架构中的信息瓶颈,TFT结合了从变换器架构继承的解码器-编码器注意力机制(Li et. al 2019,Vaswani et. al 2017)。它转化了LSTM编码的时间特征的输出,帮助解码器更好地捕捉长期关系。
每个组件的原始多头注意力 \(H_{m}\) 及其查询、键和值表示分别用 \(Q_{m}, K_{m}, V_{m}\) 表示,其变换如下:
\[\begin{align} Q_{m} = Q W_{Q,m} \quad K_{m} = K W_{K,h} \quad V_{m} = V W_{V,m} \\ H_{m}=\mathrm{Attention}(Q_{m}, K_{m}, V_{m}) = \mathrm{SoftMax}(Q_{m} K^{\intercal}_{m}/\mathrm{scale}) \; V_{m} \\ \mathrm{MultiHead}(Q, K, V) = [H_{1},\dots,H_{M}] W_{M} \end{align}\]
TFT修改了原始的多头注意力以提高其可解释性。为此,它采用共享值 \(\tilde{V}\) 来跨头使用,并采用加法聚合,\(\mathrm{InterpretableMultiHead}(Q,K,V) = \tilde{H} W_{M}\)。该机制与单个注意力层非常相似,但允许 \(M\) 个多个注意力权重,因此可以解释为 \(M\) 个单一注意力层的平均集成。
\[\begin{align} \tilde{H} &= \left(\frac{1}{M} \sum_{m} \mathrm{SoftMax}(Q_{m} K^{\intercal}_{m}/\mathrm{scale}) \right) \tilde{V} = \frac{1}{M} \sum_{m} \mathrm{Attention}(Q_{m}, K_{m}, \tilde{V}) \\ \end{align}\]
class InterpretableMultiHeadAttention(nn.Module):
def __init__(self, n_head, hidden_size, example_length, attn_dropout, dropout):
super().__init__()
self.n_head = n_head
assert hidden_size % n_head == 0
self.d_head = hidden_size // n_head
self.qkv_linears = nn.Linear(
hidden_size, (2 * self.n_head + 1) * self.d_head, bias=False
)
self.out_proj = nn.Linear(self.d_head, hidden_size, bias=False)
self.attn_dropout = nn.Dropout(attn_dropout)
self.out_dropout = nn.Dropout(dropout)
self.scale = self.d_head**-0.5
self.register_buffer(
"_mask",
torch.triu(
torch.full((example_length, example_length), float("-inf")), 1
).unsqueeze(0),
)
def forward(
self, x: Tensor, mask_future_timesteps: bool = True
) -> Tuple[Tensor, Tensor]:
# [批量大小, 时间步数, 多头注意力头数, 注意力维度] := [N, T, M, AD]
bs, t, h_size = x.shape
qkv = self.qkv_linears(x)
q, k, v = qkv.split(
(self.n_head * self.d_head, self.n_head * self.d_head, self.d_head), dim=-1
)
q = q.view(bs, t, self.n_head, self.d_head)
k = k.view(bs, t, self.n_head, self.d_head)
v = v.view(bs, t, self.d_head)
# [名词,时间1,方式,地点] x [名词,时间2,方式,地点] -> [名词,方式,时间1,时间2]
# attn_score = torch.einsum('bind,bjnd->bnij', q, k)
attn_score = torch.matmul(q.permute((0, 2, 1, 3)), k.permute((0, 2, 3, 1)))
attn_score.mul_(self.scale)
if mask_future_timesteps:
attn_score = attn_score + self._mask
attn_prob = F.softmax(attn_score, dim=3)
attn_prob = self.attn_dropout(attn_prob)
# [N,M,T1,T2] x [N,M,T1,Ad] -> [N,M,T1,Ad]
# attn_vec = torch.einsum('bnij,bjd->bnid', attn_prob, v)
attn_vec = torch.matmul(attn_prob, v.unsqueeze(1))
m_attn_vec = torch.mean(attn_vec, dim=1)
out = self.out_proj(m_attn_vec)
out = self.out_dropout(out)
return out, attn_prob2. TFT架构
第一个TFT的步骤是将原始输入\(\{\mathbf{x}^{(s)}, \mathbf{x}^{(h)}, \mathbf{x}^{(f)}\}\)嵌入到一个高维空间\(\{\mathbf{E}^{(s)}, \mathbf{E}^{(h)}, \mathbf{E}^{(f)}\}\)中,之后每个嵌入都由一个可变选择网络(VSN)进行门控。静态嵌入\(\mathbf{E}^{(s)}\)被用作变量选择的上下文以及LSTM的初始条件。最后,编码后的变量被输入到多头注意力解码器中。
\[\begin{align} c_{s}, c_{e}, (c_{h}, c_{c}) &=\textrm{StaticCovariateEncoder}(\mathbf{E}^{(s)}) \\ h_{[:t]}, h_{[t+1:t+H]} &=\textrm{TemporalCovariateEncoder}(\mathbf{E}^{(h)}, \mathbf{E}^{(f)}, c_{h}, c_{c}) \\ \hat{\mathbf{y}}^{(q)}_{[t+1:t+H]} &=\textrm{TemporalFusionDecoder}(h_{[t+1:t+H]}, c_{e}) \end{align}\]
2.1 静态协变量编码器
静态嵌入 \(\mathbf{E}^{(s)}\) 通过静态协变量编码器转换为上下文 \(c_{s}, c_{e}, c_{h}, c_{c}\)。其中 \(c_{s}\) 是时间变量选择上下文,\(c_{e}\) 是 TemporalFusionDecoder 丰富上下文,而 \(c_{h}, c_{c}\) 是用于 TemporalCovariateEncoder 的 LSTM 的隐藏/上下文。
\[\begin{align} c_{s}, c_{e}, (c_{h}, c_{c}) & = \textrm{GRN}(\textrm{VSN}(\mathbf{E}^{(s)})) \end{align}\]
class StaticCovariateEncoder(nn.Module):
def __init__(self, hidden_size, num_static_vars, dropout):
super().__init__()
self.vsn = VariableSelectionNetwork(
hidden_size=hidden_size, num_inputs=num_static_vars, dropout=dropout
)
self.context_grns = nn.ModuleList(
[
GRN(input_size=hidden_size, hidden_size=hidden_size, dropout=dropout)
for _ in range(4)
]
)
def forward(self, x: Tensor) -> Tuple[Tensor, Tensor, Tensor, Tensor]:
variable_ctx, sparse_weights = self.vsn(x)
# 上下文向量:
# 变量选择上下文
# 丰富情境
# 州_c上下文
# state_h 上下文
cs, ce, ch, cc = tuple(m(variable_ctx) for m in self.context_grns) # 类型:忽略
return cs, ce, ch, cc, sparse_weights # 类型:忽略2.2 时间协变量编码器
时间协变量编码器编码嵌入 \(\mathbf{E}^{(h)}, \mathbf{E}^{(f)}\) 和上下文 \((c_{h}, c_{c})\),使用 LSTM。
\[\begin{align} \tilde{\mathbf{E}}^{(h)}_{[:t]} & = \textrm{VSN}(\mathbf{E}^{(h)}_{[:t]}, c_{s}) \\ \tilde{\mathbf{E}}^{(h)}_{[:t]} &= \mathrm{LSTM}(\tilde{\mathbf{E}}^{(h)}_{[:t]}, (c_{h}, c_{c})) \\ h_{[:t]} &= \mathrm{Gate}(\mathrm{LayerNorm}(\tilde{\mathbf{E}}^{(h)}_{[:t]})) \end{align}\]
对未来数据重复类似的过程,主要区别在于 \(\mathbf{E}^{(f)}\) 包含未来可用的信息。
\[\begin{align} \tilde{\mathbf{E}}^{(f)}_{[t+1:t+h]} & = \textrm{VSN}(\mathbf{E}^{(h)}_{t+1:t+H}, \mathbf{E}^{(f)}_{t+1:t+H}, c_{s}) \\ \tilde{\mathbf{E}}^{(f)}_{[t+1:t+h]} &= \mathrm{LSTM}(\tilde{\mathbf{E}}^{(h)}_{[t+1:t+h]}, (c_{h}, c_{c})) \\ h_{[t+1:t+H]} &= \mathrm{Gate}(\mathrm{LayerNorm}(\tilde{\mathbf{E}}^{(f)}_{[t+1:t+h]})) \end{align}\]
class TemporalCovariateEncoder(nn.Module):
def __init__(self, hidden_size, num_historic_vars, num_future_vars, dropout):
super(TemporalCovariateEncoder, self).__init__()
self.history_vsn = VariableSelectionNetwork(
hidden_size=hidden_size, num_inputs=num_historic_vars, dropout=dropout
)
self.history_encoder = nn.LSTM(
input_size=hidden_size, hidden_size=hidden_size, batch_first=True
)
self.future_vsn = VariableSelectionNetwork(
hidden_size=hidden_size, num_inputs=num_future_vars, dropout=dropout
)
self.future_encoder = nn.LSTM(
input_size=hidden_size, hidden_size=hidden_size, batch_first=True
)
# 共享门控跳跃连接
self.input_gate = GLU(hidden_size, hidden_size)
self.input_gate_ln = LayerNorm(hidden_size, eps=1e-3)
def forward(self, historical_inputs, future_inputs, cs, ch, cc):
# [N,X_in,L] -> [N,隐藏层大小,L]
historical_features, history_vsn_sparse_weights = self.history_vsn(
historical_inputs, cs
)
history, state = self.history_encoder(historical_features, (ch, cc))
future_features, future_vsn_sparse_weights = self.future_vsn(future_inputs, cs)
future, _ = self.future_encoder(future_features, state)
# torch.cuda.synchronize() 这个调用由于未知原因提升了性能
input_embedding = torch.cat([historical_features, future_features], dim=1)
temporal_features = torch.cat([history, future], dim=1)
temporal_features = self.input_gate(temporal_features)
temporal_features = temporal_features + input_embedding
temporal_features = self.input_gate_ln(temporal_features)
return temporal_features, history_vsn_sparse_weights, future_vsn_sparse_weights2.3 时间融合解码器
时间融合解码器通过\(c_{e}\)丰富LSTM的输出,然后使用注意力层和多步适配器。 \[\begin{align} h_{[t+1:t+H]} &= \mathrm{多头注意力}(h_{[:t]}, h_{[t+1:t+H]}, c_{e}) \\ h_{[t+1:t+H]} &= \mathrm{门控}(\mathrm{层归一化}(h_{[t+1:t+H]})) \\ h_{[t+1:t+H]} &= \mathrm{门控}(\mathrm{层归一化}(\mathrm{GRN}(h_{[t+1:t+H]}))) \\ \hat{\mathbf{y}}^{(q)}_{[t+1:t+H]} &= \mathrm{多层感知机}(h_{[t+1:t+H]}) \end{align}\]
class TemporalFusionDecoder(nn.Module):
def __init__(
self, n_head, hidden_size, example_length, encoder_length, attn_dropout, dropout
):
super(TemporalFusionDecoder, self).__init__()
self.encoder_length = encoder_length
# ------------- 编码器-解码器注意力 --------------#
self.enrichment_grn = GRN(
input_size=hidden_size,
hidden_size=hidden_size,
context_hidden_size=hidden_size,
dropout=dropout,
)
self.attention = InterpretableMultiHeadAttention(
n_head=n_head,
hidden_size=hidden_size,
example_length=example_length,
attn_dropout=attn_dropout,
dropout=dropout,
)
self.attention_gate = GLU(hidden_size, hidden_size)
self.attention_ln = LayerNorm(normalized_shape=hidden_size, eps=1e-3)
self.positionwise_grn = GRN(
input_size=hidden_size, hidden_size=hidden_size, dropout=dropout
)
# ---------------------- 解码器 -----------------------#
self.decoder_gate = GLU(hidden_size, hidden_size)
self.decoder_ln = LayerNorm(normalized_shape=hidden_size, eps=1e-3)
def forward(self, temporal_features, ce):
# ------------- 编码器-解码器注意力 --------------#
# 静态富集
enriched = self.enrichment_grn(temporal_features, c=ce)
# 时间自注意力
x, atten_vect = self.attention(enriched, mask_future_timesteps=True)
# 不要计算历史分位数
x = x[:, self.encoder_length :, :]
temporal_features = temporal_features[:, self.encoder_length :, :]
enriched = enriched[:, self.encoder_length :, :]
x = self.attention_gate(x)
x = x + enriched
x = self.attention_ln(x)
# 逐位置前馈网络
x = self.positionwise_grn(x)
# ---------------------- 解码器 ----------------------#
# 最终跳跃连接
x = self.decoder_gate(x)
x = x + temporal_features
x = self.decoder_ln(x)
return x, atten_vect
class TFT(BaseWindows):
"""TFT
The Temporal Fusion Transformer architecture (TFT) is an Sequence-to-Sequence
model that combines static, historic and future available data to predict an
univariate target. The method combines gating layers, an LSTM recurrent encoder,
with and interpretable multi-head attention layer and a multi-step forecasting
strategy decoder.
**Parameters:**<br>
`h`: int, Forecast horizon. <br>
`input_size`: int, autorregresive inputs size, y=[1,2,3,4] input_size=2 -> y_[t-2:t]=[1,2].<br>
`stat_exog_list`: str list, static continuous columns.<br>
`hist_exog_list`: str list, historic continuous columns.<br>
`futr_exog_list`: str list, future continuous columns.<br>
`hidden_size`: int, units of embeddings and encoders.<br>
`dropout`: float (0, 1), dropout of inputs VSNs.<br>
`n_head`: int=4, number of attention heads in temporal fusion decoder.<br>
`attn_dropout`: float (0, 1), dropout of fusion decoder's attention layer.<br>
`shared_weights`: bool, If True, all blocks within each stack will share parameters. <br>
`activation`: str, activation from ['ReLU', 'Softplus', 'Tanh', 'SELU', 'LeakyReLU', 'PReLU', 'Sigmoid'].<br>
`loss`: PyTorch module, instantiated train loss class from [losses collection](https://nixtla.github.io/neuralforecast/losses.pytorch.html).<br>
`valid_loss`: PyTorch module=`loss`, instantiated valid loss class from [losses collection](https://nixtla.github.io/neuralforecast/losses.pytorch.html).<br>
`max_steps`: int=1000, maximum number of training steps.<br>
`learning_rate`: float=1e-3, Learning rate between (0, 1).<br>
`num_lr_decays`: int=-1, Number of learning rate decays, evenly distributed across max_steps.<br>
`early_stop_patience_steps`: int=-1, Number of validation iterations before early stopping.<br>
`val_check_steps`: int=100, Number of training steps between every validation loss check.<br>
`batch_size`: int, number of different series in each batch.<br>
`windows_batch_size`: int=None, windows sampled from rolled data, default uses all.<br>
`inference_windows_batch_size`: int=-1, number of windows to sample in each inference batch, -1 uses all.<br>
`start_padding_enabled`: bool=False, if True, the model will pad the time series with zeros at the beginning, by input size.<br>
`valid_batch_size`: int=None, number of different series in each validation and test batch.<br>
`step_size`: int=1, step size between each window of temporal data.<br>
`scaler_type`: str='robust', type of scaler for temporal inputs normalization see [temporal scalers](https://nixtla.github.io/neuralforecast/common.scalers.html).<br>
`random_seed`: int, random seed initialization for replicability.<br>
`num_workers_loader`: int=os.cpu_count(), workers to be used by `TimeSeriesDataLoader`.<br>
`drop_last_loader`: bool=False, if True `TimeSeriesDataLoader` drops last non-full batch.<br>
`alias`: str, optional, Custom name of the model.<br>
`optimizer`: Subclass of 'torch.optim.Optimizer', optional, user specified optimizer instead of the default choice (Adam).<br>
`optimizer_kwargs`: dict, optional, list of parameters used by the user specified `optimizer`.<br>
`lr_scheduler`: Subclass of 'torch.optim.lr_scheduler.LRScheduler', optional, user specified lr_scheduler instead of the default choice (StepLR).<br>
`lr_scheduler_kwargs`: dict, optional, list of parameters used by the user specified `lr_scheduler`.<br>
`**trainer_kwargs`: int, keyword trainer arguments inherited from [PyTorch Lighning's trainer](https://pytorch-lightning.readthedocs.io/en/stable/api/pytorch_lightning.trainer.trainer.Trainer.html?highlight=trainer).<br>
**References:**<br>
- [Bryan Lim, Sercan O. Arik, Nicolas Loeff, Tomas Pfister,
"Temporal Fusion Transformers for interpretable multi-horizon time series forecasting"](https://www.sciencedirect.com/science/article/pii/S0169207021000637)
"""
# 类属性
SAMPLING_TYPE = "windows"
EXOGENOUS_FUTR = True
EXOGENOUS_HIST = True
EXOGENOUS_STAT = True
def __init__(
self,
h,
input_size,
tgt_size: int = 1,
stat_exog_list=None,
hist_exog_list=None,
futr_exog_list=None,
hidden_size: int = 128,
n_head: int = 4,
attn_dropout: float = 0.0,
dropout: float = 0.1,
loss=MAE(),
valid_loss=None,
max_steps: int = 1000,
learning_rate: float = 1e-3,
num_lr_decays: int = -1,
early_stop_patience_steps: int = -1,
val_check_steps: int = 100,
batch_size: int = 32,
valid_batch_size: Optional[int] = None,
windows_batch_size: int = 1024,
inference_windows_batch_size: int = 1024,
start_padding_enabled=False,
step_size: int = 1,
scaler_type: str = "robust",
num_workers_loader=0,
drop_last_loader=False,
random_seed: int = 1,
optimizer=None,
optimizer_kwargs=None,
lr_scheduler=None,
lr_scheduler_kwargs=None,
**trainer_kwargs,
):
# 继承BaseWindows类
super(TFT, self).__init__(
h=h,
input_size=input_size,
stat_exog_list=stat_exog_list,
hist_exog_list=hist_exog_list,
futr_exog_list=futr_exog_list,
loss=loss,
valid_loss=valid_loss,
max_steps=max_steps,
learning_rate=learning_rate,
num_lr_decays=num_lr_decays,
early_stop_patience_steps=early_stop_patience_steps,
val_check_steps=val_check_steps,
batch_size=batch_size,
valid_batch_size=valid_batch_size,
windows_batch_size=windows_batch_size,
inference_windows_batch_size=inference_windows_batch_size,
start_padding_enabled=start_padding_enabled,
step_size=step_size,
scaler_type=scaler_type,
num_workers_loader=num_workers_loader,
drop_last_loader=drop_last_loader,
random_seed=random_seed,
optimizer=optimizer,
optimizer_kwargs=optimizer_kwargs,
lr_scheduler=lr_scheduler,
lr_scheduler_kwargs=lr_scheduler_kwargs,
**trainer_kwargs,
)
self.example_length = input_size + h
self.interpretability_params = dict([]) # 类型:忽略
self.tgt_size = tgt_size
futr_exog_size = max(self.futr_exog_size, 1)
num_historic_vars = futr_exog_size + self.hist_exog_size + tgt_size
#------------------------------- 编码器 -----------------------------#
self.embedding = TFTEmbedding(hidden_size=hidden_size,
stat_input_size=self.stat_exog_size,
futr_input_size=futr_exog_size,
hist_input_size=self.hist_exog_size,
tgt_size=tgt_size)
if self.stat_exog_size > 0:
self.static_encoder = StaticCovariateEncoder(
hidden_size=hidden_size,
num_static_vars=self.stat_exog_size,
dropout=dropout)
self.temporal_encoder = TemporalCovariateEncoder(
hidden_size=hidden_size,
num_historic_vars=num_historic_vars,
num_future_vars=futr_exog_size,
dropout=dropout,
)
# ------------------------------ 解码器 -----------------------------#
self.temporal_fusion_decoder = TemporalFusionDecoder(
n_head=n_head,
hidden_size=hidden_size,
example_length=self.example_length,
encoder_length=self.input_size,
attn_dropout=attn_dropout,
dropout=dropout,
)
# 具有损耗相关尺寸的适配器
self.output_adapter = nn.Linear(
in_features=hidden_size, out_features=self.loss.outputsize_multiplier
)
def forward(self, windows_batch):
# 帕西瓦尔窗口批处理
y_insample = windows_batch["insample_y"][:, :, None] # <- [B,T,1]
futr_exog = windows_batch["futr_exog"]
hist_exog = windows_batch["hist_exog"]
stat_exog = windows_batch["stat_exog"]
if futr_exog is None:
futr_exog = y_insample[:, [-1]]
futr_exog = futr_exog.repeat(1, self.example_length, 1)
s_inp, k_inp, o_inp, t_observed_tgt = self.embedding(
target_inp=y_insample,
hist_exog=hist_exog,
futr_exog=futr_exog,
stat_exog=stat_exog,
)
# -------------------------------- 输入 ------------------------------#
# 静态上下文
if s_inp is not None:
cs, ce, ch, cc, static_encoder_sparse_weights = self.static_encoder(s_inp)
ch, cc = ch.unsqueeze(0), cc.unsqueeze(0) # LSTM初始状态
else:
# 如果为空则添加零
batch_size, example_length, target_size, hidden_size = t_observed_tgt.shape
cs = torch.zeros(size=(batch_size, hidden_size), device=y_insample.device)
ce = torch.zeros(size=(batch_size, hidden_size), device=y_insample.device)
ch = torch.zeros(
size=(1, batch_size, hidden_size), device=y_insample.device
)
cc = torch.zeros(
size=(1, batch_size, hidden_size), device=y_insample.device
)
static_encoder_sparse_weights = []
# 历史输入
_historical_inputs = [
k_inp[:, : self.input_size, :],
t_observed_tgt[:, : self.input_size, :],
]
if o_inp is not None:
_historical_inputs.insert(0, o_inp[:, : self.input_size, :])
historical_inputs = torch.cat(_historical_inputs, dim=-2)
# 未来输入
future_inputs = k_inp[:, self.input_size :]
# ---------------------------- 编码/解码 ---------------------------#
# 嵌入 + 视觉语义嵌入网络 + 长短期记忆编码器
temporal_features, history_vsn_wgts, future_vsn_wgts = self.temporal_encoder(
historical_inputs=historical_inputs,
future_inputs=future_inputs,
cs=cs,
ch=ch,
cc=cc,
)
# 静态富集、注意力机制与解码器
temporal_features, attn_wts = self.temporal_fusion_decoder(
temporal_features=temporal_features, ce=ce
)
# 存储参数
self.interpretability_params = {
"history_vsn_wgts": history_vsn_wgts,
"future_vsn_wgts": future_vsn_wgts,
"static_encoder_sparse_weights": static_encoder_sparse_weights,
"attn_wts": attn_wts,
}
# 适应输出以减少损失
y_hat = self.output_adapter(temporal_features)
y_hat = self.loss.domain_map(y_hat)
return y_hat
def mean_on_batch(self, tensor):
batch_size = tensor.size(0)
if batch_size > 1:
return tensor.mean(dim=0)
else:
return tensor.squeeze(0)
def feature_importances(self):
"""
Compute the feature importances for historical, future, and static features.
Returns:
dict: A dictionary containing the feature importances for each feature type.
The keys are 'hist_vsn', 'future_vsn', and 'static_vsn', and the values
are pandas DataFrames with the corresponding feature importances.
"""
if not self.interpretability_params:
raise ValueError(
"No interpretability_params. Make a prediction using the model to generate them."
)
importances = {}
# 历史特征重要性
hist_vsn_wgts = self.interpretability_params.get("history_vsn_wgts")
hist_exog_list = list(self.hist_exog_list) + list(self.futr_exog_list)
hist_exog_list += (
[f"observed_target_{i+1}" for i in range(self.tgt_size)]
if self.tgt_size > 1
else ["observed_target"]
)
hist_vsn_imp = pd.DataFrame(
self.mean_on_batch(hist_vsn_wgts).cpu().numpy(), columns=hist_exog_list
)
importances["Past variable importance over time"] = hist_vsn_imp
# importances["Past variable importance"] = hist_vsn_imp.mean(axis=0).sort_values()
# 未来特征重要性
if self.futr_exog_size > 0:
future_vsn_wgts = self.interpretability_params.get("future_vsn_wgts")
future_vsn_imp = pd.DataFrame(
self.mean_on_batch(future_vsn_wgts).cpu().numpy(), columns=self.futr_exog_list
)
importances["Future variable importance over time"] = future_vsn_imp
# importances["Future variable importance"] = future_vsn_imp.mean(axis=0).sort_values()
# 静态特征重要性
if self.stat_exog_size > 0:
static_encoder_sparse_weights = self.interpretability_params.get(
"static_encoder_sparse_weights"
)
static_vsn_imp = pd.DataFrame(
self.mean_on_batch(static_encoder_sparse_weights).cpu().numpy(),
index=self.stat_exog_list,
columns=["importance"],
)
importances["Static covariates"] = static_vsn_imp.sort_values(
by="importance"
)
return importances
def attention_weights(self):
"""
批量平均注意力权重
返回值:
np.ndarray: 一个一维数组,包含每个时间步的注意力权重。
"""
attention = (
self.mean_on_batch(self.interpretability_params["attn_wts"])
.mean(dim=0)
.cpu()
.numpy()
)
return attention
def feature_importance_correlations(self)-> pd.DataFrame:
"""
Compute the correlation between the past and future feature importances and the mean attention weights.
Returns:
pd.DataFrame: A DataFrame containing the correlation coefficients between the past feature importances and the mean attention weights.
"""
attention = self.attention_weights()[self.input_size :, :].mean(axis=0)
p_c = self.feature_importances()["Past variable importance over time"]
p_c["Correlation with Mean Attention"] = attention[: self.input_size]
return p_c.corr(method="spearman").round(2)3. TFT 方法
show_doc(TFT.fit, name='TFT.fit', title_level=3)TFT.fit
TFT.fit (dataset, val_size=0, test_size=0, random_seed=None, distributed_config=None)
*Fit.
The fit method, optimizes the neural network’s weights using the initialization parameters (learning_rate, windows_batch_size, …) and the loss function as defined during the initialization. Within fit we use a PyTorch Lightning Trainer that inherits the initialization’s self.trainer_kwargs, to customize its inputs, see PL’s trainer arguments.
The method is designed to be compatible with SKLearn-like classes and in particular to be compatible with the StatsForecast library.
By default the model is not saving training checkpoints to protect disk memory, to get them change enable_checkpointing=True in __init__.
Parameters:
dataset: NeuralForecast’s TimeSeriesDataset, see documentation.
val_size: int, validation size for temporal cross-validation.
random_seed: int=None, random_seed for pytorch initializer and numpy generators, overwrites model.__init__’s.
test_size: int, test size for temporal cross-validation.
*
show_doc(TFT.predict, name='TFT.predict', title_level=3)TFT.predict
TFT.predict (dataset, test_size=None, step_size=1, random_seed=None, **data_module_kwargs)
*Predict.
Neural network prediction with PL’s Trainer execution of predict_step.
Parameters:
dataset: NeuralForecast’s TimeSeriesDataset, see documentation.
test_size: int=None, test size for temporal cross-validation.
step_size: int=1, Step size between each window.
random_seed: int=None, random_seed for pytorch initializer and numpy generators, overwrites model.__init__’s.
**data_module_kwargs: PL’s TimeSeriesDataModule args, see documentation.*
show_doc(TFT.feature_importances, name='TFT.feature_importances,', title_level=3)TFT.feature_importances,
TFT.feature_importances, ()
*Compute the feature importances for historical, future, and static features.
Returns: dict: A dictionary containing the feature importances for each feature type. The keys are ‘hist_vsn’, ‘future_vsn’, and ‘static_vsn’, and the values are pandas DataFrames with the corresponding feature importances.*
show_doc(TFT.attention_weights , name='TFT.attention_weights', title_level=3)TFT.attention_weights
TFT.attention_weights ()
*Batch average attention weights
Returns: np.ndarray: A 1D array containing the attention weights for each time step.*
show_doc(TFT.attention_weights , name='TFT.attention_weights', title_level=3)TFT.attention_weights
TFT.attention_weights ()
*Batch average attention weights
Returns: np.ndarray: A 1D array containing the attention weights for each time step.*
show_doc(TFT.feature_importance_correlations , name='TFT.feature_importance_correlations', title_level=3)TFT.feature_importance_correlations
TFT.feature_importance_correlations ()
*Compute the correlation between the past and future feature importances and the mean attention weights.
Returns: pd.DataFrame: A DataFrame containing the correlation coefficients between the past feature importances and the mean attention weights.*
使用示例
import pandas as pd
import matplotlib.pyplot as plt
import numpy as np
from neuralforecast import NeuralForecast
#从neuralforecast.models模块中导入TFT
from neuralforecast.losses.pytorch import DistributionLoss
from neuralforecast.utils import AirPassengersPanel, AirPassengersStatic
AirPassengersPanel['month']=AirPassengersPanel.ds.dt.month
Y_train_df = AirPassengersPanel[AirPassengersPanel.ds<AirPassengersPanel['ds'].values[-12]] # 132次列车
Y_test_df = AirPassengersPanel[AirPassengersPanel.ds>=AirPassengersPanel['ds'].values[-12]].reset_index(drop=True) # 12项测试
nf = NeuralForecast(
models=[TFT(h=12, input_size=48,
hidden_size=20,
loss=DistributionLoss(distribution='StudentT', level=[80, 90]),
learning_rate=0.005,
stat_exog_list=['airline1'],
futr_exog_list=['y_[lag12]','month'],
hist_exog_list=['trend'],
max_steps=300,
val_check_steps=10,
early_stop_patience_steps=10,
scaler_type='robust',
windows_batch_size=None,
enable_progress_bar=True),
],
freq='M'
)
nf.fit(df=Y_train_df, static_df=AirPassengersStatic, val_size=12)
Y_hat_df = nf.predict(futr_df=Y_test_df)
# 绘制分位数预测图
Y_hat_df = Y_hat_df.reset_index(drop=False).drop(columns=['unique_id','ds'])
plot_df = pd.concat([Y_test_df, Y_hat_df], axis=1)
plot_df = pd.concat([Y_train_df, plot_df])
plot_df = plot_df[plot_df.unique_id=='Airline1'].drop('unique_id', axis=1)
plt.plot(plot_df['ds'], plot_df['y'], c='black', label='True')
plt.plot(plot_df['ds'], plot_df['TFT'], c='purple', label='mean')
plt.plot(plot_df['ds'], plot_df['TFT-median'], c='blue', label='median')
plt.fill_between(x=plot_df['ds'][-12:],
y1=plot_df['TFT-lo-90'][-12:].values,
y2=plot_df['TFT-hi-90'][-12:].values,
alpha=0.4, label='level 90')
plt.legend()
plt.grid()
plt.plot()Seed set to 1
可解释性
1. 注意力权重
attention = nf.models[0].attention_weights()def plot_attention(self, plot:str="time", output:str='plot', width:int=800, height:int=400):
"""
Plot the attention weights.
Args:
plot (str, optional): The type of plot to generate. Can be one of the following:
- 'time': Display the mean attention weights over time.
- 'all': Display the attention weights for each horizon.
- 'heatmap': Display the attention weights as a heatmap.
- An integer in the range [1, model.h) to display the attention weights for a specific horizon.
output (str, optional): The type of output to generate. Can be one of the following:
- 'plot': Display the plot directly.
- 'figure': Return the plot as a figure object.
width (int, optional): Width of the plot in pixels. Default is 800.
height (int, optional): Height of the plot in pixels. Default is 400.
Returns:
matplotlib.figure.Figure: If `output` is 'figure', the function returns the plot as a figure object.
"""
attention = (
self.mean_on_batch(self.interpretability_params["attn_wts"])
.mean(dim=0)
.cpu()
.numpy()
)
fig, ax = plt.subplots(figsize=(width / 100, height / 100))
if plot == "time":
attention = attention[self.input_size:, :].mean(axis=0)
ax.plot(np.arange(-self.input_size, self.h), attention)
ax.axvline(x=0, color='black', linewidth=3, linestyle='--', label="prediction start")
ax.set_title("Mean Attention")
ax.set_xlabel("time")
ax.set_ylabel("Attention")
ax.legend()
elif plot == "all":
for i in range(self.input_size, attention.shape[0]):
ax.plot(np.arange(-self.input_size, self.h), attention[i, :], label=f"horizon {i-self.input_size+1}")
ax.axvline(x=0, color='black', linewidth=3, linestyle='--', label="prediction start")
ax.set_title("Attention per horizon")
ax.set_xlabel("time")
ax.set_ylabel("Attention")
ax.legend()
elif plot == "heatmap":
cax = ax.imshow(attention, aspect='auto', cmap='viridis',
extent=[-self.input_size, self.h, -self.input_size, self.h])
fig.colorbar(cax)
ax.set_title("Attention Heatmap")
ax.set_xlabel("Attention (current time step)")
ax.set_ylabel("Attention (previous time step)")
elif isinstance(plot, int) and (plot in np.arange(1, self.h + 1)):
i = self.input_size + plot - 1
ax.plot(np.arange(-self.input_size, self.h), attention[i, :], label=f"horizon {plot}")
ax.axvline(x=0, color='black', linewidth=3, linestyle='--', label="prediction start")
ax.set_title(f"Attention weight for horizon {plot}")
ax.set_xlabel("time")
ax.set_ylabel("Attention")
ax.legend()
else:
raise ValueError('plot has to be in ["time","all","heatmap"] or integer in range(1,model.h)')
plt.tight_layout()
if output == 'plot':
plt.show()
elif output == 'figure':
return fig
else:
raise ValueError(f"Invalid output: {output}. Expected 'plot' or 'figure'.")1.1 平均注意力
plot_attention(nf.models[0], plot="time")
1.2 所有未来时间步骤的注意力
plot_attention(nf.models[0], plot="all")
1.3 特定未来时间步的注意力
plot_attention(nf.models[0], plot=8)
2. 特征重要性
2.1 全局特征重要性
feature_importances = nf.models[0].feature_importances()
feature_importances.keys()dict_keys(['Past variable importance over time', 'Future variable importance over time', 'Static covariates'])静态变量重要性
feature_importances['Static covariates'].sort_values(by='importance').plot(kind='barh')
过去的变量重要性
feature_importances['Past variable importance over time'].mean().sort_values().plot(kind='barh')
未来变量的重要性
feature_importances['Future variable importance over time'].mean().sort_values().plot(kind='barh')
2.2 随时间变化的变量重要性
未来变量随时间的重要性
每个未来协变量在每个未来时间步的的重要性
df=feature_importances['Future variable importance over time']
fig, ax = plt.subplots(figsize=(20, 10))
bottom = np.zeros(len(df.index))
for col in df.columns:
p = ax.bar(np.arange(-len(df),0), df[col].values, 0.6, label=col, bottom=bottom)
bottom += df[col]
ax.set_title('Future variable importance over time ponderated by attention')
ax.set_ylabel("Importance")
ax.set_xlabel("Time")
ax.grid(True)
ax.legend()
plt.show()
请提供需要翻译的ipynb文件的具体内容,我将帮助您进行翻译。
随时间变化的过去变量重要性
df= feature_importances['Past variable importance over time']
fig, ax = plt.subplots(figsize=(20, 10))
bottom = np.zeros(len(df.index))
for col in df.columns:
p = ax.bar(np.arange(-len(df),0), df[col].values, 0.6, label=col, bottom=bottom)
bottom += df[col]
ax.set_title('Past variable importance over time')
ax.set_ylabel("Importance")
ax.set_xlabel("Time")
ax.legend()
ax.grid(True)
plt.show()
随时间变化的过去变量重要性,基于注意力进行加权
基于各时间步上变量的重要性,对每个时间步的重要性进行分解。
df= feature_importances['Past variable importance over time']
mean_attention = nf.models[0].attention_weights()[nf.models[0].input_size:,:].mean(axis=0)[:nf.models[0].input_size]
df = df.multiply(mean_attention, axis=0)
fig, ax = plt.subplots(figsize=(20, 10))
bottom = np.zeros(len(df.index))
for col in df.columns:
p = ax.bar(np.arange(-len(df),0), df[col].values, 0.6, label=col, bottom=bottom)
bottom += df[col]
ax.set_title('Past variable importance over time ponderated by attention')
ax.set_ylabel("Importance")
ax.set_xlabel("Time")
ax.legend()
ax.grid(True)
plt.plot(np.arange(-len(df),0), mean_attention, color='black', marker='o', linestyle='-', linewidth=2, label='mean_attention')
plt.legend()
plt.show()
3. 随时间变化的变量重要性相关性
在同一时刻获得和失去重要性的变量
nf.models[0].feature_importance_correlations()| trend | y_[lag12] | month | observed_target | Correlation with Mean Attention | |
|---|---|---|---|---|---|
| trend | 1.00 | -0.39 | -0.93 | 0.27 | 0.60 |
| y_[lag12] | -0.39 | 1.00 | 0.37 | -0.93 | -0.76 |
| month | -0.93 | 0.37 | 1.00 | -0.37 | -0.66 |
| observed_target | 0.27 | -0.93 | -0.37 | 1.00 | 0.77 |
| Correlation with Mean Attention | 0.60 | -0.76 | -0.66 | 0.77 | 1.00 |
Give us a ⭐ on Github