参数化函数

限定名称: manim.mobject.graphing.functions.ParametricFunction

class ParametricFunction(function, t_range=(0, 1), scaling=<manim.mobject.graphing.scale.LinearBase object>, dt=1e-08, discontinuities=None, use_smoothing=True, use_vectorized=False, **kwargs)

基础类: VMobject

参数曲线。

Parameters:

• function (Callable[[float], Point3D]) – 以(lambda t: (x(t), y(t), z(t)))形式绘制的函数

• t_range (Point2D | Point3D) – 确定函数在 (t_min, t_max, step=0.01) 形式下的跨度长度。默认情况下为 [0, 1]

• scaling (_ScaleBase) – 应用于函数点的缩放类。默认为 LinearBase。

• use_smoothing (bool) – 是否在函数点创建后在它们之间进行插值。 （在点数较少时可能会有奇怪的行为）

• use_vectorized (bool) – 是否将生成的 t 值数组作为 [t_0, t_1, ...] 传递给函数。 只有在你的函数支持时才使用此选项。输出应该是一个形状为 [[x_0, x_1, ...], [y_0, y_1, ...], [z_0, z_1, ...]] 的 numpy 数组，但如果 Axes 是 2D 的，z 也可以为 0。

• 不连续点 (可迭代[浮点数] | 无) – 函数在这些 t 值处出现不连续。

• dt (float) – 不连续性的左右容差。

示例

示例：PlotParametricFunction

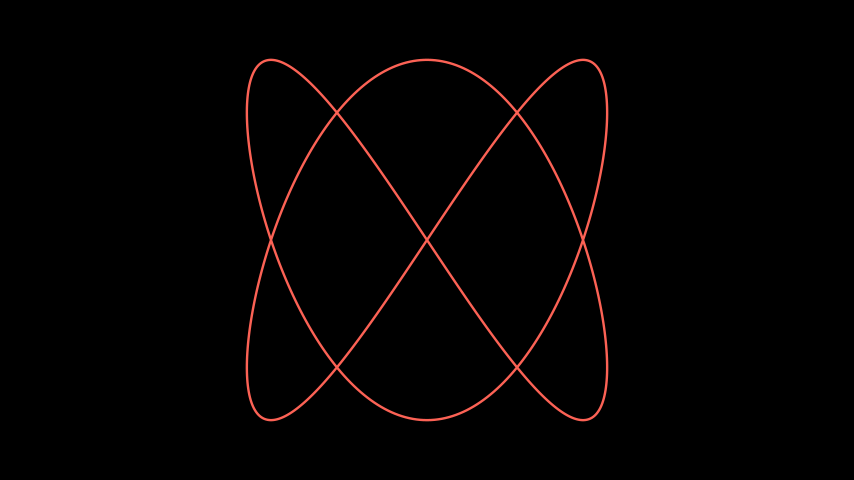
from manim import *

class PlotParametricFunction(Scene):
    def func(self, t):
        return (np.sin(2 * t), np.sin(3 * t), 0)

    def construct(self):
        func = ParametricFunction(self.func, t_range = (0, TAU), fill_opacity=0).set_color(RED)
        self.add(func.scale(3))

class PlotParametricFunction(Scene):
    def func(self, t):
        return (np.sin(2 * t), np.sin(3 * t), 0)

    def construct(self):
        func = ParametricFunction(self.func, t_range = (0, TAU), fill_opacity=0).set_color(RED)
        self.add(func.scale(3))

示例：ThreeDParametricSpring

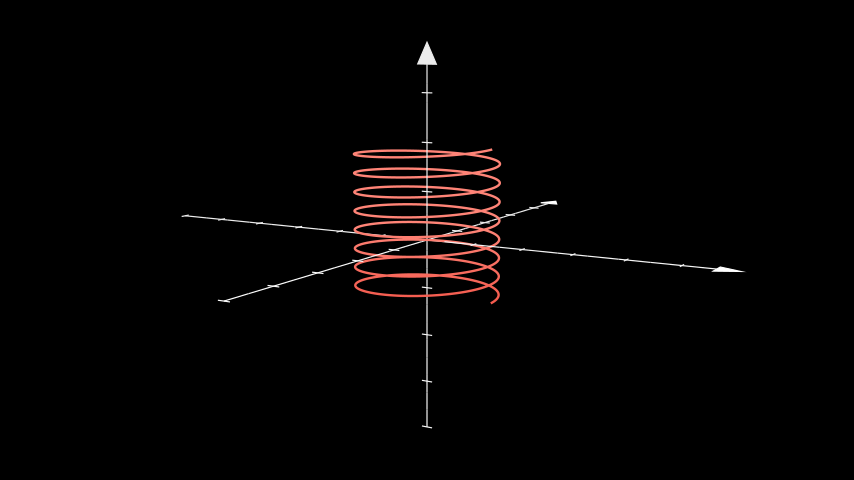
from manim import *

class ThreeDParametricSpring(ThreeDScene):
    def construct(self):
        curve1 = ParametricFunction(
            lambda u: (
                1.2 * np.cos(u),
                1.2 * np.sin(u),
                u * 0.05
            ), color=RED, t_range = (-3*TAU, 5*TAU, 0.01)
        ).set_shade_in_3d(True)
        axes = ThreeDAxes()
        self.add(axes, curve1)
        self.set_camera_orientation(phi=80 * DEGREES, theta=-60 * DEGREES)
        self.wait()

class ThreeDParametricSpring(ThreeDScene):
    def construct(self):
        curve1 = ParametricFunction(
            lambda u: (
                1.2 * np.cos(u),
                1.2 * np.sin(u),
                u * 0.05
            ), color=RED, t_range = (-3*TAU, 5*TAU, 0.01)
        ).set_shade_in_3d(True)
        axes = ThreeDAxes()
        self.add(axes, curve1)
        self.set_camera_orientation(phi=80 * DEGREES, theta=-60 * DEGREES)
        self.wait()

注意

如果你的函数有不连续点，你需要手动指定不连续点的位置。请参考以下示例以获取指导。

示例：不连续示例

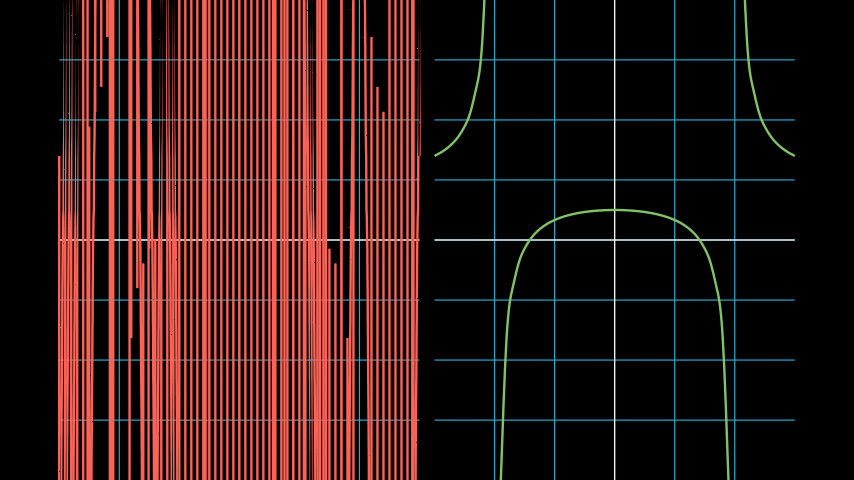
from manim import *

class DiscontinuousExample(Scene):
    def construct(self):
        ax1 = NumberPlane((-3, 3), (-4, 4))
        ax2 = NumberPlane((-3, 3), (-4, 4))
        VGroup(ax1, ax2).arrange()
        discontinuous_function = lambda x: (x ** 2 - 2) / (x ** 2 - 4)
        incorrect = ax1.plot(discontinuous_function, color=RED)
        correct = ax2.plot(
            discontinuous_function,
            discontinuities=[-2, 2],  # discontinuous points
            dt=0.1,  # left and right tolerance of discontinuity
            color=GREEN,
        )
        self.add(ax1, ax2, incorrect, correct)

class DiscontinuousExample(Scene):
    def construct(self):
        ax1 = NumberPlane((-3, 3), (-4, 4))
        ax2 = NumberPlane((-3, 3), (-4, 4))
        VGroup(ax1, ax2).arrange()
        discontinuous_function = lambda x: (x ** 2 - 2) / (x ** 2 - 4)
        incorrect = ax1.plot(discontinuous_function, color=RED)
        correct = ax2.plot(
            discontinuous_function,
            discontinuities=[-2, 2],  # discontinuous points
            dt=0.1,  # left and right tolerance of discontinuity
            color=GREEN,
        )
        self.add(ax1, ax2, incorrect, correct)

方法

generate_points	初始化 points 并因此确定形状。
get_function
get_point_from_function
init_points	初始化 points 并因此确定形状。

属性

animate	用于动画化self的任何方法的应用。
animation_overrides
color
depth	mobject的深度。
fill_color	如果有多种颜色（用于渐变），则返回第一个颜色
height	mobject的高度。
n_points_per_curve
sheen_factor
stroke_color
width	mobject的宽度。

_original__init__(function, t_range=(0, 1), scaling=<manim.mobject.graphing.scale.LinearBase object>, dt=1e-08, discontinuities=None, use_smoothing=True, use_vectorized=False, **kwargs)

初始化自身。有关准确的签名，请参阅 help(type(self))。

Parameters:

• function (Callable[[float], Point3D])

• t_range (Point2D | Point3D)

• 缩放 (_ScaleBase)

• dt (float)

• 不连续点 (可迭代[浮点数] | 无)

• use_smoothing (bool)

• use_vectorized (bool)

generate_points()

初始化 points 并因此确定形状。

在创建时调用。这是一个可以由子类实现的空方法。

init_points()

初始化 points 并因此确定形状。

在创建时调用。这是一个可以由子类实现的空方法。