pymc.Beta#
- class pymc.Beta(name, *args, rng=None, dims=None, initval=None, observed=None, total_size=None, transform=UNSET, **kwargs)[源代码]#
Beta 对数似然。
此分布的pdf是
\[f(x \mid \alpha, \beta) = \frac{x^{\alpha - 1} (1 - x)^{\beta - 1}}{B(\alpha, \beta)}\]其中 \(B\) 是 Beta 函数。
更多信息,请参见 https://en.wikipedia.org/wiki/Beta_distribution。
(
Source code,png,hires.png,pdf)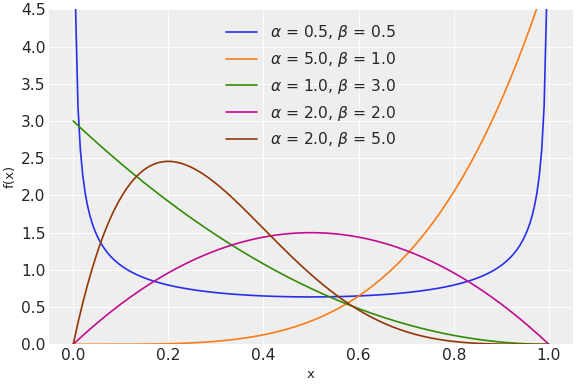
支持
\(x \in (0, 1)\)
均值
\(\dfrac{\alpha}{\alpha + \beta}\)
方差
\(\dfrac{\alpha \beta}{(\alpha+\beta)^2(\alpha+\beta+1)}\)
贝塔分布可以用alpha和beta、均值和标准差或均值和样本量来参数化。三种参数化之间的联系由以下公式给出:
\[ \begin{align}\begin{aligned}\begin{split}\alpha &= \mu \kappa \\ \beta &= (1 - \mu) \kappa\end{split}\\\text{其中 } \kappa = \frac{\mu(1-\mu)}{\sigma^2} - 1\\\alpha = \mu * \nu \beta = (1 - \mu) * \nu\end{aligned}\end{align} \]- 参数:
- alpha : 类似张量 的
float, 可选tensor_like 的 python:float, 可选 alpha> 0。如果未指定,则使用mu和sigma计算。- beta : 类似张量 的
float,可选tensor_like 的 python:float, 可选 beta> 0。如果未指定,则使用mu和sigma计算。- mu : 类似张量 的
float, 可选tensor_like 的 python:float, 可选 替代均值 (0 <
mu< 1)。- sigma : 类似张量 的
float, 可选tensor_like 的 python:float, 可选 替代标准差 (0 <
sigma< sqrt(mu* (1 -mu)))。- nu : 类似张量 的
float, 可选tensor_like 的 python:float, 可选 Beta 分布的替代“样本量”(
nu> 0)。
- alpha : 类似张量 的
注释
Beta 分布是二项分布参数 \(p\) 的共轭先验。
方法
Beta.dist([alpha, beta, mu, sigma, nu])创建一个与 cls 分布相对应的张量变量。