pymc.DiscreteWeibull

class pymc.DiscreteWeibull(name, *args, **kwargs)

离散威布尔对数似然。

离散威布尔分布是一个灵活的计数数据模型，可以处理过度分散和欠分散的情况。该分布的概率质量函数为

\[f(x \mid q, \beta) = q^{x^{\beta}} - q^{(x + 1)^{\beta}}\]

(Source code, png, hires.png, pdf)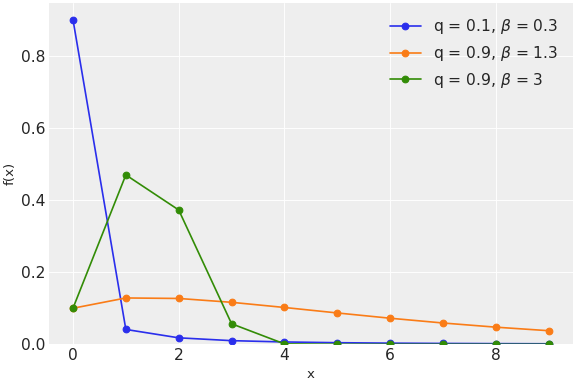

支持	\(x \in \mathbb{N}_0\)
均值	\(\mu = \sum_{x = 1}^{\infty} q^{x^{\beta}}\)
方差	\(2 \sum_{x = 1}^{\infty} x q^{x^{\beta}} - \mu - \mu^2\)

参数:

q : 类似张量 的 floattensor_like of float

形状参数 (0 < q < 1)。

beta : 类似张量 的 floattensor_like of float

形状参数（beta > 0）。

方法

DiscreteWeibull.dist(q, beta, *args, **kwargs)

创建一个与 cls 分布相对应的张量变量。