pymc.LogNormal#

class pymc.LogNormal(name, *args, rng=None, dims=None, initval=None, observed=None, total_size=None, transform=UNSET, **kwargs)[源代码]#

对数正态对数似然。

任何对数正态分布的随机变量的分布。如果一个变量可以被认为是许多独立小因子的乘积，那么它可以被建模为对数正态分布。

注意：类名 Lognormal 已弃用，请使用 LogNormal！

此分布的pdf是

\[f(x \mid \mu, \tau) = \frac{1}{x} \sqrt{\frac{\tau}{2\pi}} \exp\left\{ -\frac{\tau}{2} (\ln(x)-\mu)^2 \right\}\]

(Source code, png, hires.png, pdf)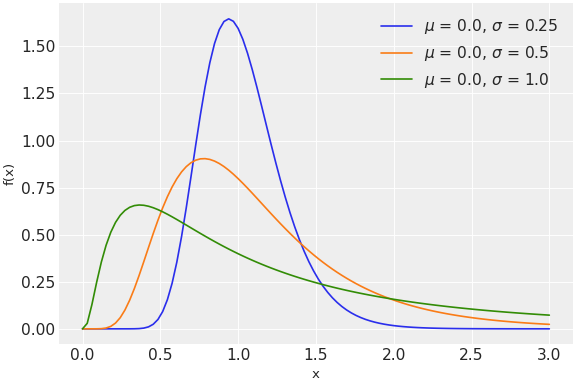

../../../_images/pymc-LogNormal-1.png

支持

\(x \in [0, \infty)\)

均值

\(\exp\{\mu + \frac{1}{2\tau}\}\)

方差

\((\exp\{\frac{1}{\tau}\} - 1) \times \exp\{2\mu + \frac{1}{\tau}\}\)
参数:
mu : 类张量 的 float，默认值为 0tensor_like of python:float, 默认值为 0

位置参数。

sigma : 类似张量 的 float, 可选tensor_like of python:float, 可选

标准差。（sigma > 0）。（仅在未指定 tau 时需要）。默认为 1。

tau : 类似张量 的 float, 可选tensor_like of python:float, 可选

尺度参数（tau > 0）。（仅在未指定 sigma 时需要）。默认为 1。

示例

# Example to show that we pass in only ``sigma`` or ``tau`` but not both.
with pm.Model():
    x = pm.LogNormal('x', mu=2, sigma=30)

with pm.Model():
    x = pm.LogNormal('x', mu=2, tau=1/100)

方法

LogNormal.dist([mu, sigma, tau])

创建一个与 cls 分布相对应的张量变量。