pymc.零膨胀二项分布

class pymc.ZeroInflatedBinomial(name, psi, n, p, **kwargs)

零膨胀二项式对数似然。

该分布的概率质量函数是

\[\begin{split}f(x \mid \psi, n, p) = \left\{ \begin{array}{l} (1-\psi) + \psi (1-p)^{n}, \text{若 } x = 0 \\ \psi {n \choose x} p^x (1-p)^{n-x}, \text{若 } x=1,2,3,\ldots,n \end{array} \right.\end{split}\]

(Source code, png, hires.png, pdf)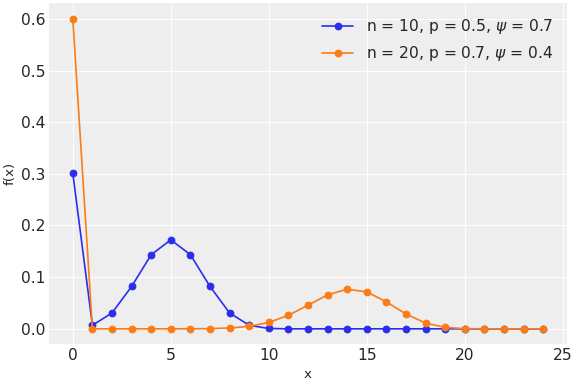

支持	\(x \in \mathbb{N}_0\)
均值	\(\psi n p\)
方差	\((1-\psi) n p [1 - p(1 - \psi n)].\)

参数:

psi : 类似张量 的 floattensor_like of float

二项式变量的预期比例 (0 < psi < 1)

n : 类似张量 的 intpython:int 的 tensor_like

伯努利试验的次数（n >= 0）。

p : 类张量 的 floattensor_like of float

每次试验成功的概率 (0 < p < 1)。

方法

ZeroInflatedBinomial.dist(psi, n, p, **kwargs)