pymc.ExGaussian#

class pymc.ExGaussian(name, *args, rng=None, dims=None, initval=None, observed=None, total_size=None, transform=UNSET, **kwargs)[源代码]#

指数修正高斯对数似然。

正态分布与指数分布卷积的结果。

此分布的pdf是

\[f(x \mid \mu, \sigma, \tau) = \frac{1}{\nu}\; \exp\left\{\frac{\mu-x}{\nu}+\frac{\sigma^2}{2\nu^2}\right\} \Phi\left(\frac{x-\mu}{\sigma}-\frac{\sigma}{\nu}\right)\]

其中 \(\Phi\) 是标准正态分布的累积分布函数。

(Source code, png, hires.png, pdf)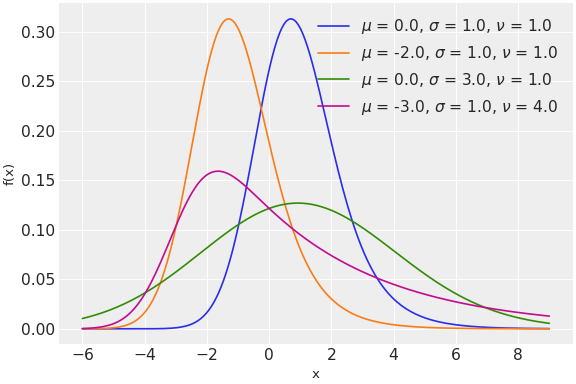

../../../_images/pymc-ExGaussian-1.png

支持

\(x \in \mathbb{R}\)

均值

\(\mu + \nu\)

方差

\(\sigma^2 + \nu^2\)
参数:
mu : 类张量 的 float，默认值为 0tensor_like of python:float, 默认值为 0

正态分布的均值。

sigma : 类似张量 的 floattensor_like of float

正态分布的标准差（sigma > 0）。

nu : 类张量 的 floattensor_like of float

指数分布的均值（nu > 0）。

参考文献

[Rigby2005]

Rigby R.A. 和 Stasinopoulos D.M. (2005). “位置、尺度和形状的广义加性模型” 应用统计学., 54, 第3部分, 第507-554页。

[Lacouture2008]

Lacouture, Y. 和 Couseanou, D. (2008). “如何使用 MATLAB 拟合 ex-Gaussian 和其他概率函数到反应时间分布”。心理学定量方法教程，第 4 卷，第 1 期，第 35-45 页。

方法

ExGaussian.dist([mu, sigma, nu])

创建一个与 cls 分布相对应的张量变量。