pymc.PolyaGamma

class pymc.PolyaGamma(name, *args, rng=None, dims=None, initval=None, observed=None, total_size=None, transform=UNSET, **kwargs)

Polya-Gamma 分布。

该分布由 ``h``（形状参数）和 ``z``（指数倾斜参数）参数化。该分布的概率密度函数为

\[f(x \mid h, z) = cosh^h(\frac{z}{2})e^{-\frac{1}{2}xz^2}f(x \mid h, 0),\]

其中 \(f(x \mid h, 0)\) 是 \(PG(h, 0)\) 变量的概率密度函数。注意，该分布的概率密度函数表示为逆高斯密度函数的交替符号和。

\[X = \Sigma_{k=1}^{\infty}\frac{Ga(h, 1)}{d_k},\]

其中 \(d_k = 2(k - 0.5)^2\pi^2 + z^2/2\)，\(Ga(h, 1)\) 是形状参数为 h 和尺度参数为 1 的伽马随机变量。

(Source code, png, hires.png, pdf)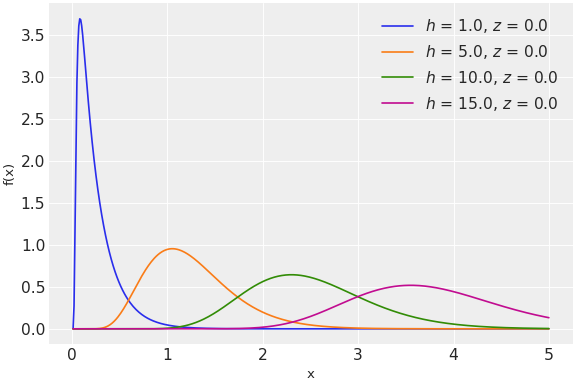

支持	\(x \in (0, \infty)\)
均值	\(\dfrac{h}{4}\) 如果 \(z=0\), \(\dfrac{tanh(z/2)h}{2z}\) 否则。
方差	\(0.041666688h\) 如果 \(z=0\), \(\dfrac{h(sinh(z) - z)(1 - tanh^2(z/2))}{4z^3}\) 否则。

参数:

h : 类似张量 的 float，默认值为 1tensor_like of python:float, 默认值为 1

分布的形状参数（h > 0）。

z : 类似张量 的 float，默认值为 0tensor_like of python:float, 默认值为 0

分布的指数倾斜参数。

参考文献

[1]

Polson, Nicholas G., James G. Scott, 和 Jesse Windle. “使用Pólya–Gamma潜变量的逻辑模型贝叶斯推断.” 美国统计协会杂志 108.504 (2013): 1339-1349.

[2]

Windle, Jesse, Nicholas G. Polson, 和 James G. Scott. “采样 Polya-Gamma 随机变量：替代和近似技术.” arXiv 预印本 arXiv:1405.0506 (2014).

[3]

Luc Devroye. “关于与雅可比θ函数相关的某些分布的精确模拟算法。” 《统计与概率通讯》，第79卷，第21期，（2009年）：2251-2259。

[4]

Windle, J. (2013). 使用高频数据预测高维、时变方差-协方差矩阵以及从逻辑似然推导的后验分布中采样Pólya-Gamma随机变量。(博士论文)。检索自 http://hdl.handle.net/2152/21842

示例

rng = np.random.default_rng()
with pm.Model():
    x = pm.PolyaGamma('x', h=1, z=5.5)
with pm.Model():
    x = pm.PolyaGamma('x', h=25, z=-2.3, rng=rng, size=(100, 5))

方法

PolyaGamma.dist([h, z])

创建一个与 cls 分布相对应的张量变量。