pymc.NegativeBinomial

class pymc.NegativeBinomial(name, *args, **kwargs)

负二项对数似然。

负二项分布描述了一个速率参数为伽马分布的泊松随机变量。其概率质量函数（pmf）由伽马分布的参数 alpha 和 mu 参数化，为

\[f(x \mid \mu, \alpha) = \binom{x + \alpha - 1}{x} (\alpha/(\mu+\alpha))^\alpha (\mu/(\mu+\alpha))^x\]

(Source code, png, hires.png, pdf)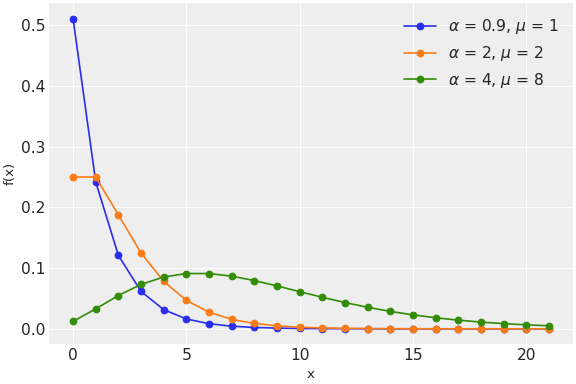

支持	\(x \in \mathbb{N}_0\)
均值	\(\mu\)
方差	\(\frac{\mu^2}{\alpha} + \mu\)

负二项分布可以用 mu 或 p 来参数化，也可以用 alpha 或 n 来参数化。参数化之间的关系由以下公式给出：

\[\begin{split}p &= \frac{\alpha}{\mu + \alpha} \\ n &= \alpha\end{split}\]

如果它是以 n 和 p 为参数的，负二项分布描述了在第 n 次成功之前有 x 次失败的概率，给定每次试验成功的概率为 p。其概率质量函数为

\[f(x \mid n, p) = \binom{x + n - 1}{x} (p)^n (1 - p)^x\]

参数:

alpha : 类似张量 的 floattensor_like of float

伽马分布形状参数（alpha > 0）。

mu : 类似张量 的 floattensor_like of float

Gamma 分布均值（mu > 0）。

p : 类张量 的 floattensor_like of float

每次试验中成功的替代概率（0 < p < 1）。

n : 类似张量 的 floattensor_like of float

目标成功试验的替代次数（n > 0）

方法

NegativeBinomial.dist([mu, alpha, p, n])

创建一个与 cls 分布相对应的张量变量。