pymc.StudentT#

class pymc.StudentT(name, *args, rng=None, dims=None, initval=None, observed=None, total_size=None, transform=UNSET, **kwargs)[源代码]#

学生 T 对数似然。

描述一个精度服从伽马分布的普通变量。如果仅传递了 nu 参数，则指定一个标准（中心）学生 T 分布。

此分布的pdf是

\[f(x|\mu,\lambda,\nu) = \frac{\Gamma(\frac{\nu + 1}{2})}{\Gamma(\frac{\nu}{2})} \left(\frac{\lambda}{\pi\nu}\right)^{\frac{1}{2}} \left[1+\frac{\lambda(x-\mu)^2}{\nu}\right]^{-\frac{\nu+1}{2}}\]

(Source code, png, hires.png, pdf)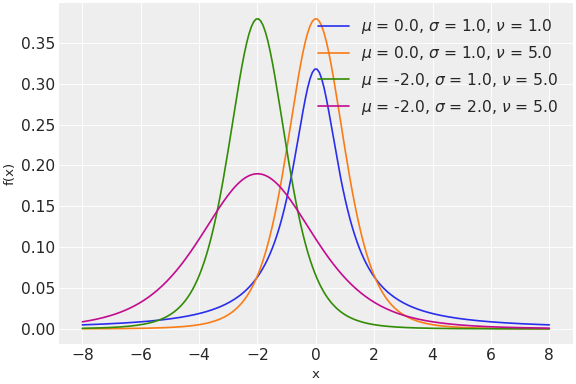

../../../_images/pymc-StudentT-1.png

支持

\(x \in \mathbb{R}\)
参数:
nu : 类张量 的 floattensor_like of float

自由度，也称为正态参数（nu > 0）。

mu : 类张量 的 float，默认值为 0tensor_like of python:float, 默认值为 0

位置参数。

sigma : 类似张量 的 float, 可选tensor_like 的 python:float, 可选

尺度参数（sigma > 0）。随着 nu 的增加，趋向于标准差（仅在未指定 lam 时需要）。默认为 1。

lam : 类似张量 的 float, 可选tensor_like 的 python:float, 可选

尺度参数 (lam > 0)。随着 nu 的增加，收敛到精度（仅在未指定 sigma 时需要）。默认为 1。

示例

with pm.Model():
    x = pm.StudentT('x', nu=15, mu=0, sigma=10)

with pm.Model():
    x = pm.StudentT('x', nu=15, mu=0, lam=1/23)

方法

StudentT.dist(nu[, mu, sigma, lam])

创建一个与 cls 分布相对应的张量变量。