pymc.Wald#

class pymc.Wald(name, *args, rng=None, dims=None, initval=None, observed=None, total_size=None, transform=UNSET, **kwargs)[源代码]#

Wald 对数似然。

此分布的pdf是

\[f(x \mid \mu, \lambda) = \left(\frac{\lambda}{2\pi}\right)^{1/2} x^{-3/2} \exp\left\{ -\frac{\lambda}{2x}\left(\frac{x-\mu}{\mu}\right)^2 \right\}\]

(Source code, png, hires.png, pdf)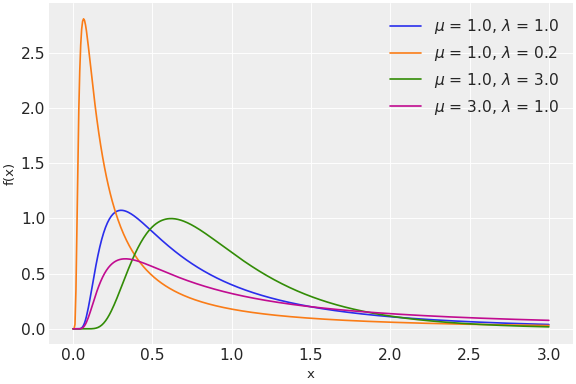

../../../_images/pymc-Wald-1.png

支持

\(x \in (0, \infty)\)

均值

\(\mu\)

方差

\(\dfrac{\mu^3}{\lambda}\)

Wald 分布可以用 lam 或 phi 来参数化。这两种参数化之间的联系由以下公式给出

\[\phi = \dfrac{\lambda}{\mu}\]
参数:
mu : 类似张量 的 float, 可选tensor_like 的 python:float, 可选

分布的均值（mu > 0）。

lam : 类似张量 的 float, 可选tensor_like 的 python:float, 可选

相对精度（lam > 0）。

phi : 类似张量 的 float，可选tensor_like 的 python:float, 可选

替代形状参数（phi > 0）。

alpha : 类似张量 的 float，默认值为 0tensor_like of python:float, 默认值为 0

位移/位置参数（alpha >= 0）。

注释

要实例化分布，请指定以下任意一项

  • 只有 mu (在这种情况下 lam 将为 1)

  • mu 和 lam

  • mu 和 phi

  • lam 和 phi

参考文献

[Tweedie1957]

Tweedie, M. C. K. (1957). 逆高斯分布的统计性质 I. 数理统计年刊, 第28卷, 第2期, 第362-377页

[Michael1976]

Michael, J. R., Schucany, W. R. 和 Hass, R. W. (1976)。使用具有多重根的变换生成随机变量。《美国统计学家》，第30卷，第2期，第88-90页

[Giner2016]

Göknur Giner, Gordon K. Smyth (2016) statmod: 逆高斯分布的概率计算

方法

Wald.dist([mu, lam, phi, alpha])

创建一个与 cls 分布相对应的张量变量。