pymc.Rice#

class pymc.Rice(name, *args, rng=None, dims=None, initval=None, observed=None, total_size=None, transform=UNSET, **kwargs)[源代码]#

大米分配。

\[ \begin{align}\begin{aligned}f(x\mid \nu ,\sigma )= {\frac {x}{\sigma ^{2}}}\exp \left({\frac {-(x^{2}+\nu ^{2})}{2\sigma ^{2}}}\right)I_{0}\left({\frac {x\nu }{\sigma ^{2}}}\right),\\f(x\mid \nu ,\sigma )= {\frac {x}{\sigma ^{2}}}\exp \left({\frac {-(x^{2}+\nu ^{2})}{2\sigma ^{2}}}\right)I_{0}\left({\frac {x\nu }{\sigma ^{2}}}\right),\end{aligned}\end{align} \]

(Source code, png, hires.png, pdf)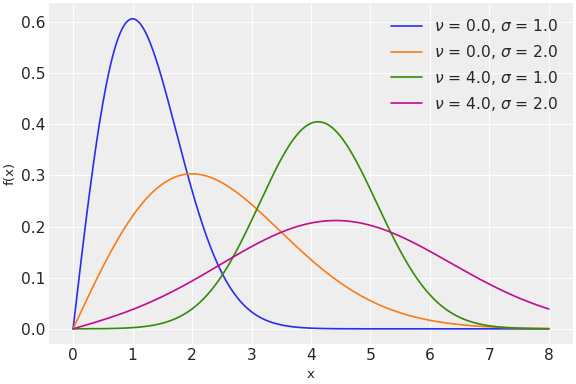

../../../_images/pymc-Rice-1.png

支持

\(x \in (0, \infty)\)

均值

\(\sigma {\sqrt {\pi /2}}\,\,L_{{1/2}}(-\nu ^{2}/2\sigma ^{2})\)

方差

\(2\sigma ^{2}+\nu ^{2}-{\frac {\pi \sigma ^{2}}{2}}L_{{1/2}}^{2}\left({\frac {-\nu ^{2}}{2\sigma ^{2}}}\right)\)
参数:
nu : 类似张量 的 float, 可选tensor_like 的 python:float, 可选

非中心性参数（仅在未指定 b 时需要）。

sigma : 类似张量 的 float，默认值为 1tensor_like of python:float, 默认值为 1

比例参数。

b : 类似张量 的 float，可选tensor_like 的 python:float, 可选

形状参数（nu 的替代项，仅在未指定 nu 时需要）。

注释

分布 \(\mathrm{Rice}\left(|\nu|,\sigma\right)\) 是 \(R=\sqrt{X^2+Y^2}\) 的分布，其中 \(X\sim N(\nu \cos{\theta}, \sigma^2)\)，\(Y\sim N(\nu \sin{\theta}, \sigma^2)\) 是独立的，并且对于任何实数 \(\theta\)。

分布可以用 nu 或 b 来定义。这两种参数化之间的联系由以下公式给出：

\[b = \dfrac{\nu}{\sigma}\]

方法

Rice.dist([nu, sigma, b])

创建一个与 cls 分布相对应的张量变量。