pymc.Logistic

class pymc.Logistic(name, *args, rng=None, dims=None, initval=None, observed=None, total_size=None, transform=UNSET, **kwargs)

逻辑对数似然。

此分布的PDF是

\[f(x \mid \mu, s) = \frac{\exp\left(-\frac{x - \mu}{s}\right)}{s \left(1 + \exp\left(-\frac{x - \mu}{s}\right)\right)^2}\]

(Source code, png, hires.png, pdf)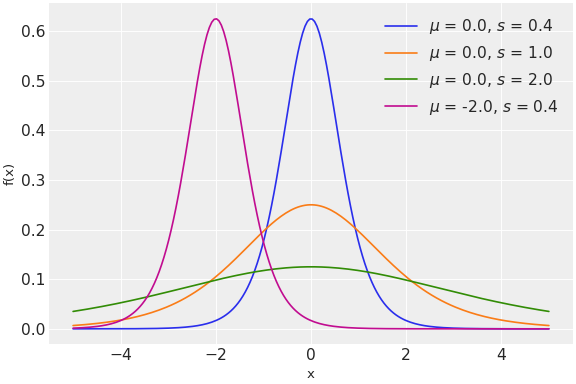

支持	\(x \in \mathbb{R}\)
均值	\(\mu\)
方差	\(\frac{s^2 \pi^2}{3}\)

参数:

mu : 类张量 的 float，默认值为 0python:float 类型的 tensor_like，默认为 0

平均值。

s : 类似张量 的 float，默认值为 1tensor_like of python:float, 默认值为 1

比例 (s > 0)。

方法

Logistic.dist([mu, s])

创建一个与 cls 分布相对应的张量变量。